Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@koji_nakano(中野 浩嗣)

正確な確率の並列ルーレット選択

Last updated at Posted at 2024-03-25

ポイント

  • ルーレット選択を並列処理で高速かつ正確に行うLogarithmic Random Bidding手法の紹介です．
  • Independentルーレット選択は高速にルーレット選択を行えますが，適応度の小さいものを選ばれる確率が極端に低くなる問題点がありました．Logarithmic Random Bidding手法はこれを解決し，正確な確率でルーレット選択を行います．

ルーレット選択

ルーレット選択とは，複数のアイテムに非負実数の適応度(fitness)が与えられている状況で，その中から一つを適応度に比例した確率で選ぶ操作です．形式的には，$n$個のアイテム$0, 1, \ldots, n-1$に適応度$f_0, f_1, \ldots, f_{n-1}$ ($f_i\geq 0$)が割り当てられているときに，アイテム$i$を次の確率$F_i$で選びます：
$$
F_i = \frac{f_i}{f_0+f_1+\cdots+f_{n-1}}
$$

ルーレット選択は，下の図のような円グラフの面積を各アイテムの適応度に比例して設定し、ランダムにダーツを投げてアイテムを選択することに相当します

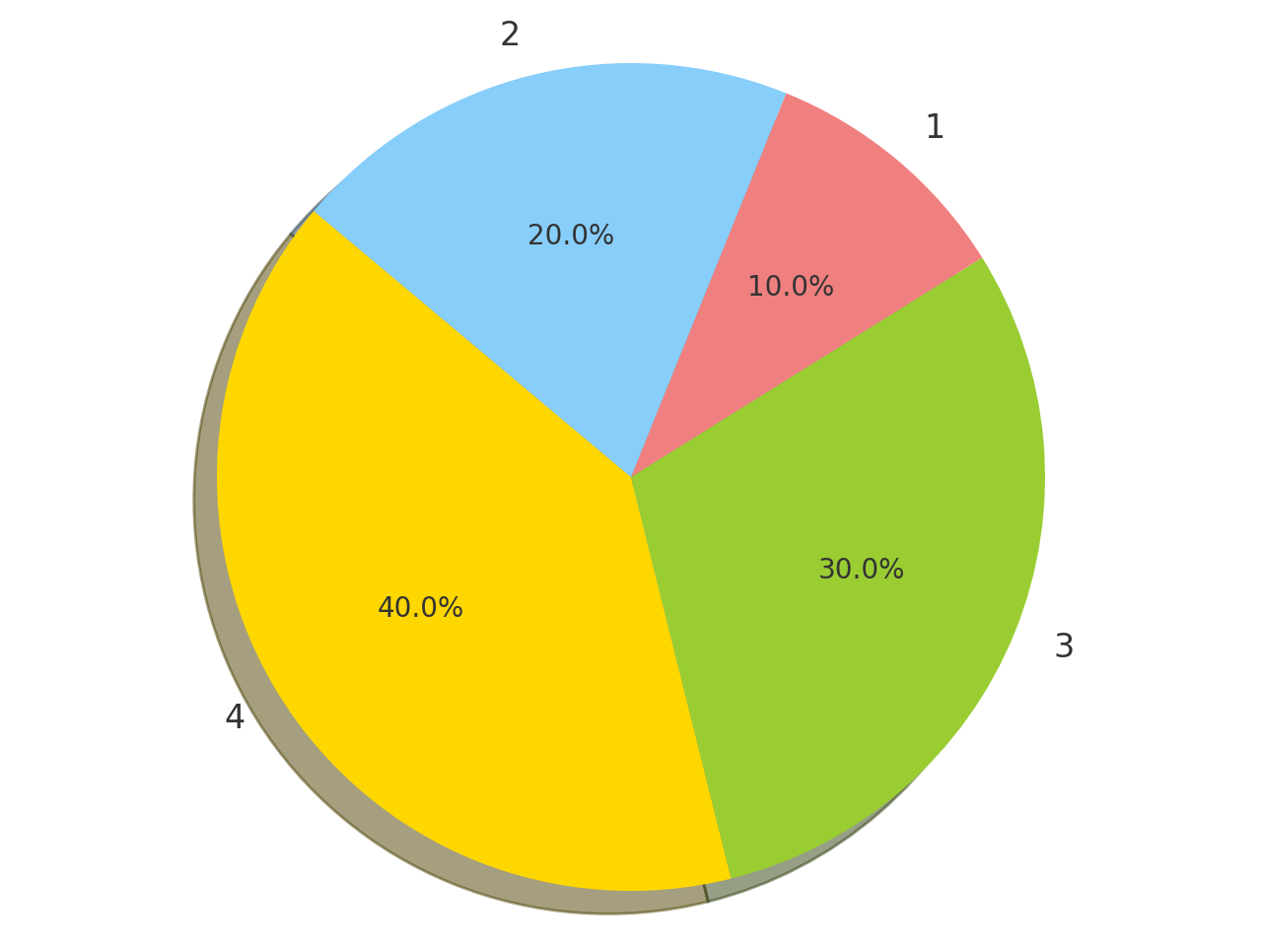
ルーレット選択は、最適化問題を解く際のヒューリスティックなアルゴリズムに頻繁に用いられます．例えば，巡回セールスマン問題を解く蟻コロニー最適化では，都市間の辺に適応度が割り当てられ，次に訪れる都市をルーレット選択で決定します．

ルーレット選択の自明な方法

次に定義される適応度の接頭部和(prefix-sums)$p_0, p_1, \ldots, p_{n-1}$を求めます．
$$
p_i = f_0+f_1+\cdots+f_{i}
$$
簡単のため，$p_{-1}=0$とします．接頭部和は，以下のアルゴリズムで容易に求めることができます．

for i=0 to n-1 do 
  p[i] = p[i-1] + f[i]$

次に，0以上1 未満の一様乱数を返す関数 $rand()$ を用いて $r = rand() * p_{n-1}$ を計算します．ここで，$p_{n-1}$ は全適応度の合計に相当します．そして、$p_{i-1} \leq r < p_{i}$ を満たす $i$ を2分探索で見つけ出し，アイテム $i$ を選択します．アイテム $i$ を選ぶ確率は，
$$
\frac{p_{i}-p_{i-1}}{p_{n-1}}=\frac{f_i}{p_{n-1}}=F_i
$$
となり，これにより，正しい確率でルーレット選択が行われていることが示されます．以下のテーブルはアイテム数が5の場合の例です．この自明な方法の正しさが確認できます．

$i$ 0 1 2 3 4
$f_i$ 4 0 3 1 2
$F_i$ 0.4 0.0 0.3 0.1 0.2
$p_i$ 4 4 7 8 10
$\frac{p_{i}-p_{i-1}}{p_{n-1}}$ $\frac{4}{10}$ $\frac{0}{10}$ $\frac{3}{10}$ $\frac{1}{10}$ $\frac{2}{10}$

並列ルーレット選択

複数のプロセッサやスレッドを用いて，並列処理によりルーレット選択を行う状況を想定します．簡単のため，$n$個のスレッド$0, 1, \ldots, n-1$に適応度$f_0, f_1, \ldots, f_{n-1}$ ($f_i\geq 0$)が割り当てられているものとし，スレッド $i$ を確率 $p_i$ で選択する操作を並列ルーレット選択と呼びます．例えば，蟻コロニー最適化を並列処理によって高速化する場合，スレッドが都市間の辺に割り当てられ，適応度に比例した確率で次の訪問都市（つまりスレッド）を選択する状況が想定されます．

接頭部和は並列処理により，理論的に$O(\log n)$時間で求めることができます．高速ではありますが，計算処理が複雑です．また，適応度$f_i$の大半が0の場合でも同じ計算コストがかかります．蟻コロニー最適化では，既訪問の都市に向かう辺の適応度は0として選ばれないようにするので，実行の過程で多くの適応度が0になります．したがって，適応度$f_i$の大半が0の場合に計算コストが小さくなることは重要です．

Independentルーレット選択

Independentルーレット選択は，処理が単純で，かつ適応度$f_i$の大半が0の場合には処理時間が大幅に短縮できる手法です．各スレッド$i$は，$f_i>0$の場合のみ動作し，$r_i=rand()*f_i$を計算します．$r_i$は0以上$f_i$未満の一様乱数となります．そして，すべての計算された$r_i$から最大のものを選び，選ばれた$r_i$をもつスレッドをルーレット選択の結果とします．つまり，次の式を満たすスレッド$i$を選びます．
$$
r_i = \max(r_0,r_1, \ldots, r_{n-1})
$$

最大の$r_i$を選ぶのに，GPUなどがサポートしているアトミック演算atomicMaxを利用すれば$f_i$の大半が0の場合には特に高速です．適切に並列実装を行うことで，$f_i$のうち非ゼロのものの個数を$k$とすると，平均$O(\log k)$時間で最大の$r_i$を選ぶことができます．

適応度$f_i$が大きいほど，計算される$r_i$が大きくなりやすいので，適応度の高いスレッドほど高い確率で選ばれるのが直感的に理解できます．しかし，選ばれる確率は$F_i$と必ずしも一致しません．特に，$f_i$が全体の最小値の場合は，選ばれる確率は$F_i$より著しく低くなることがあります．例えば，$n=10$で$f_0=1$，$f_1=f_2=\cdots=f_{9}=2$の場合の確率を計算します．ルーレット選択では，スレッド0が選ばれる確率は，$\frac{1}{19}\approx 0.0526$，それ以外の各スレッドが選ばれる確率は$\frac{2}{19}\approx 0.1052$となるはずです．しかし，$r_0$の範囲は$[0,1)$，それ以外の$r_i$は$[0,2)$の範囲でランダムに決定されます．したがって，スレッド0が選ばれるためには，少なくとも$r_1, r_2, \ldots, r_{9}$がすべて1未満となる条件下で，$r_0$が最大でなければならないため、実際の確率は，$2^{-9}\times \frac{1}{10}=\frac{1}{5120}\approx 0.000195$と非常に低くなってしまいます．

Logarithmic Random Bidding手法

Logarithmic Random Bidding手法は，Independentルーレット選択と同様のアプローチを取りますが，異なるのは$r_i$の計算方法です．$r_i=rand()*f_i$ではなく，$r_i=\frac{\log(rand())}{f_i}$と計算します．ここで$\log(rand())$は負の値を取るため，$f_i$が大きければ大きいほど、$r_i$は大きな値を取り，その結果スレッド$i$が選択されやすくなります。

スレッド$i$が選ばれる確率は，比較的簡単に計算することができます．まず，$r_i$の累積分布関数は次のように計算されます．

\Pr(r_i\leq x) = \Pr\Bigr(\frac{\log(rand())}{f_i}\leq x\Bigl) = \Pr(rand()\leq e^{xf_i}) = e^{xf_i}

これは$r_i$が$x$以下となる確率が$e^{xf_i}$であることを示しています．したがって、$r_i$の確率密度関数は微分を行い以下のように求められます．

\frac{d\Pr(r_i\leq x)}{dx} = f_ie^{xf_i}

これは，微小区間$\Delta x$に対して，$r_i$の値が$x$から$x + \Delta x$の間にある確率を$\Delta x$で割ると、$f_ie^{xf_i}$となることを意味しています．したがって，スレッド0が選ばれる確率，つまり，$r_0$が最小となる確率は次のように計算され，$F_0$となります．他のスレッド$i$が選ばれる確率も同様に$F_i$となります．

\begin{align}
\int_{-\infty}^0 \frac{d\Pr(r_0\leq x)}{dx}\cdot\Pr(r_1\leq x)\cdots \Pr(r_{n-1}\leq x)dx &= \int_{-\infty}^0 f_0 e^{x(f_0+f_1+\cdots+f_{n-1})}dx\\
&=\Bigr[\frac{f_0}{f_0+f_1+\cdots+f_{n-1}}e^{x(f_0+f_1+\cdots+f_{n-1})}\Bigl]_{-\infty}^0\\
&=\frac{f_0}{f_0+f_1+\cdots+f_{n-1}} \\
& = F_0
\end{align}

積分内の式は，$r_0$が$x$から$x + \Delta x$の範囲の値を取り，同時に他の$r_i$が$x$以下の値を取る確率を$\Delta x$で割ったものを示しています．ここで$x$は$-\infty$から$0$まで変化します．この積分は．全ての$r_i$の中で$r_0$が最も大きな値を取る，すなわちスレッド0が選ばれる確率を計算しています．

シミュレーション

$f_0=1$, $f_1=f_2=\cdots=f_9=2$の場合のシミュレーションを行うC++プログラムです．randomNumberを計算する行をコメントにより選択することで，IndependentとLogarithmic Random Biddingを切り替えることができます．選ばれたスレッドのヒストグラムを求め出力します．

#include <cmath>
#include <iostream>
#include <limits>
#include <random>
#include <vector>

int main(int argc, char *argv[]) {
  const int totalTrials = 100000000;
  const int Size = 10;
  double f[Size];

  for (int i = 0; i < Size; ++i) {
    if (i == 0)
      f[i] = 1;
    else
      f[i] = 2;
  }
  std::vector<int> histogram(Size, 0);
  std::mt19937 gen(0);
  std::uniform_real_distribution<> dis(0.0, 1.0);

  for (int i = 0; i < totalTrials; ++i) {
    double maxNumber = std::numeric_limits<double>::lowest();
    int maxindex;
    for (int j = 0; j < Size; ++j) {
      double randomNumber = dis(gen) * f[j];
      //  double randomNumber = log(dis(gen)) / f[j];
      if (j == 0 || randomNumber > maxNumber) {
        maxNumber = randomNumber;
        maxindex = j;
      }
    }
    histogram[maxindex]++;
  }

  for (int i = 0; i < Size; ++i) {
    std::cout << i << ":" << histogram[i] << std::endl;
  }
}

Independentの場合の出力です．0を選んだ確率が理論値の $0.000195...$と合致しており，ルーレット選択が要求する確率$0.0526...$に比べてかなり小さくなっています．

0:19550
1:11111136
2:11107982
3:11116758
4:11106942
5:11103372
6:11112208
7:11102835
8:11110704
9:11108513

Logarithmic Random Biddingの場合の出力です．0を選んだ確率が理論値の$0.0526...$に近く，ルーレット選択が求める確率とあっています．

0:5265929
1:10527607
2:10525182
3:10533844
4:10524026
5:10520449
6:10528520
7:10520722
8:10527276
9:10526445

おわりに

最適化問題を解くをヒューリスティックアルゴリズムにおいて，選択の良さを適応度としてそれに比例した確率で決定するルーレット選択は，よく行われる有効な方法です．Logarithmic Random Bidding手法はルーレット選択を並列処理で高速化する際に効果を発揮する有望な手法です．

参考文献

Independentルーレット選択

  • Independentルーレット選択：José M. Cecilia, José M. García, Andy Nisbet, Martyn Amos, Manuel Ujaldón, Enhancing data parallelism for Ant Colony Optimization on GPUs, Journal of Parallel and Distributed Computing, Volume 73, Issue 1, January 2013, Pages 42-51, 2013 (DOI)
  • Independentルーレット選択の確率評価：Huw Lloyd, Martyn Amos, Analysis of independent roulette selection in parallel ant colony optimization, GECCO '17: Proceedings of the Genetic and Evolutionary Computation Conference, 2017 (DOI)

Logarithmic Random Bidding

  • Logarithmic Random Biddingの提案：Koji Nakano, The Logarithmic Random Bidding for the Parallel Roulette Wheel Selection with Precise Probabilities, to appear in Proc. of International Symposium on Parallel and Distributed Systems Workshops, 2024 (arXiv)

追記

Liink.aiというサイトに上のarXivの論文をもとに，AIが生成したと思われる解説が掲載されています．ここには、重要な点が抜けていたり、少し誤解を招く表現が含まれている部分もあります．しかし，後半の「Deeper Inquiries」のところは，arXivの論文のIntroductionにこのような内容を書けば，より大きなインパクトを読者に与えることができたのではないかと感じました．

3
1
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?