はじめに
今回は統計検定2級の第1種過誤と第2種過誤について学んでいきます!!あ〜、偽陽性とか偽陰性とかのやつね位の理解だったので、ちゃんと学んでいこうと思います!!
🎓 第1種過誤と第2種過誤とは?
🔹 第1種過誤(α)
帰無仮説 ( H_0 ) が本当なのに、間違って棄却してしまうこと。
例:本当は無罪なのに「有罪」と誤って判決を出してしまう
🔸 第2種過誤(β)
対立仮説 ( H_1 ) が本当なのに、間違って採用せずに帰無仮説のままにしてしまうこと。
例:本当は有罪なのに「無罪」としてしまう
| 現実\判断 | H₀を採用 | H₀を棄却 |
|---|---|---|
| H₀が正しい | 正しい判断 | 第1種過誤(α) |
| H₁が正しい | 第2種過誤(β) | 正しい判断 |
🧪 例題:第1種過誤の確率を求めよ
ある商品の重量 ( X ) は以下の正規分布に従うとします:
$$
X \sim N(\theta, 4)
$$
この商品が「平均500gか、510gか」を検定したいと考えています。
仮説:
- ( H_0: \theta = 500 )
- ( H_1: \theta = 510 )
検定ルール:
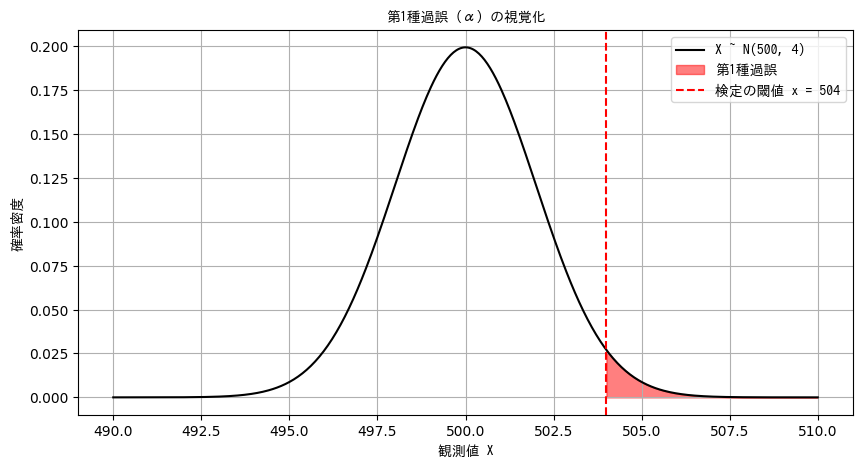
「X ≧ 504 なら H₀ を棄却する」
❓ 問題:
このとき、第1種過誤(α)の確率はいくつか?
選択肢:
- ① 0.1587
- ② 0.3085
- ③ 0.2266
- ④ 0.0668
- ⑤ 0.4013
✅ 解説
帰無仮説が正しいとき(θ = 500)には:
$$
X \sim N(500, 4)
$$
このときの第1種過誤は:
$$
P(X \geq 504 \mid \theta = 500)
$$
▶ 標準化(Zスコア):
$$
Z = \frac{504 - 500}{2} = 2
$$
▶ 標準正規分布の右側の確率:
$$
P(Z \geq 2) = 1 - \Phi(2) \approx 1 - 0.9772 = 0.0228
$$
🎯 正解:
$$
\boxed{0.0228}
$$
選択肢に近いものがない場合は、正確な値を使って検定設計することが大切です。
# 📌 Colab専用:日本語フォントのインストール
!apt-get -y install fonts-ipafont-gothic > /dev/null
# 📦 ライブラリ
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from matplotlib.font_manager import FontProperties
# 🎌 フォント設定(必ずインストール後に設定)
jp_font = FontProperties(fname="/usr/share/fonts/opentype/ipafont-gothic/ipag.ttf")
plt.rcParams["font.family"] = jp_font.get_name()
# 📈 パラメータ
mu = 500
sigma = 2
x = np.linspace(490, 510, 500)
y = norm.pdf(x, loc=mu, scale=sigma)
# 🖍 図の描画
plt.figure(figsize=(10, 5))
plt.plot(x, y, label='X ~ N(500, 4)', color='black')
# 🔴 第1種過誤部分の塗りつぶし
x_fill = np.linspace(504, 510, 200)
plt.fill_between(x_fill, norm.pdf(x_fill, mu, sigma), color='red', alpha=0.5, label='第1種過誤')
# 🎯 補助線とラベル
plt.axvline(504, color='red', linestyle='--', label='検定の閾値 x = 504')
plt.title('第1種過誤(α)の視覚化', fontproperties=jp_font)
plt.xlabel('観測値 X', fontproperties=jp_font)
plt.ylabel('確率密度', fontproperties=jp_font)
plt.legend(prop=jp_font)
plt.grid(True)
plt.show()
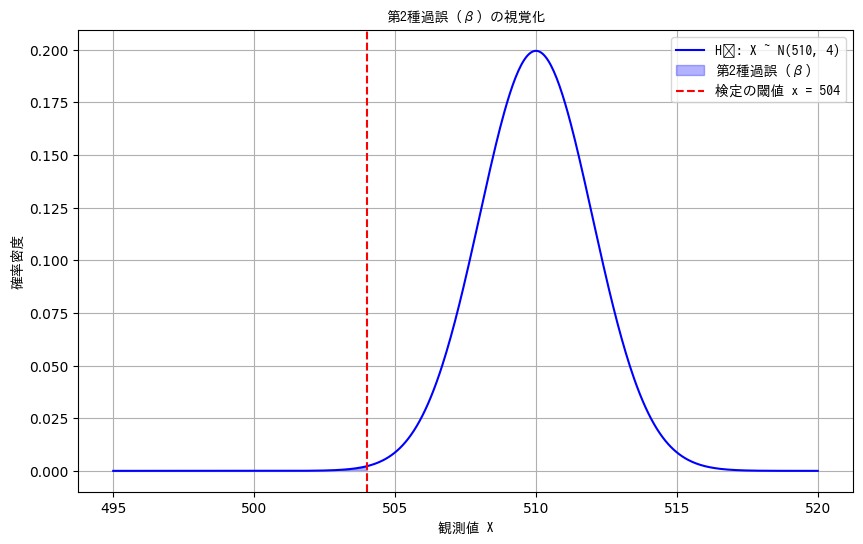
🔸 第2種過誤(β)
対立仮説 ( H_1 ) が正しい(θ = 510)のに、
Xが 504 より小さくなってしまって H₀ を誤って採用してしまう確率:
$$
P(X < 504 \mid \theta = 510)
$$
Zスコアに標準化:
$$
Z = \frac{504 - 510}{2} = -3
$$
標準正規分布での確率:
$$
P(Z < -3) = \Phi(-3) \approx 0.0013
$$
→ よって、第2種過誤の確率は:
$$
\boxed{\beta = 0.0013}
$$
# 📌 Google Colab専用:日本語フォントのインストール
!apt-get -y install fonts-ipafont-gothic > /dev/null
# 📦 必要なライブラリ
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from matplotlib.font_manager import FontProperties
# 🎌 日本語フォント設定
jp_font = FontProperties(fname="/usr/share/fonts/opentype/ipafont-gothic/ipag.ttf")
plt.rcParams["font.family"] = jp_font.get_name()
# 📊 パラメータ
mu1 = 510 # 対立仮説 H1 の平均
sigma = 2
threshold = 504 # 検定の閾値
x = np.linspace(495, 520, 500)
# 分布の密度関数(H1が正しい世界)
y1 = norm.pdf(x, loc=mu1, scale=sigma)
# 🖍 図の描画
plt.figure(figsize=(10, 6))
# 分布描画(H1: 平均510)
plt.plot(x, y1, label='H₁: X ~ N(510, 4)', color='blue')
# 🟦 第2種過誤(H₁が正しいのにH₀を採用)
x_beta = np.linspace(495, threshold, 300)
plt.fill_between(x_beta, norm.pdf(x_beta, mu1, sigma), color='blue', alpha=0.3, label='第2種過誤(β)')
# 閾値ライン
plt.axvline(threshold, color='red', linestyle='--', label='検定の閾値 x = 504')
# ラベルとスタイル
plt.title('第2種過誤(β)の視覚化', fontproperties=jp_font)
plt.xlabel('観測値 X', fontproperties=jp_font)
plt.ylabel('確率密度', fontproperties=jp_font)
plt.legend(prop=jp_font)
plt.grid(True)
plt.show()
✨ まとめ
| 過誤の種類 | 意味 | 今回の確率 |
|---|---|---|
| 第1種過誤(α) | H₀が正しいのに棄却してしまう | 0.0228 |
| 第2種過誤(β) | H₁が正しいのに棄却できず、H₀をそのままにしてしまう | 0.0013 |