はじめに
Rを学びたいStep20です。前回までに標準正規分布の振り返りを実施していました。標準化することで異なるデータでも比較できるようになりました。
ただ、標準化することで、なぜ確率や統計に生きてくるのか?分布を作っただけでは確率とは関係ないよね?🤔ってことが腑に落ちないので、今回学んでいこうと思います。
「標準化して比較する」話からなぜ「確率」の話につながるのか?
さて表題通り、なぜ正規分布が確率の話につながるのか。ここを理解していこうと思います。
前回までの話では、標準化すると下記のような分布になることがわかっています。
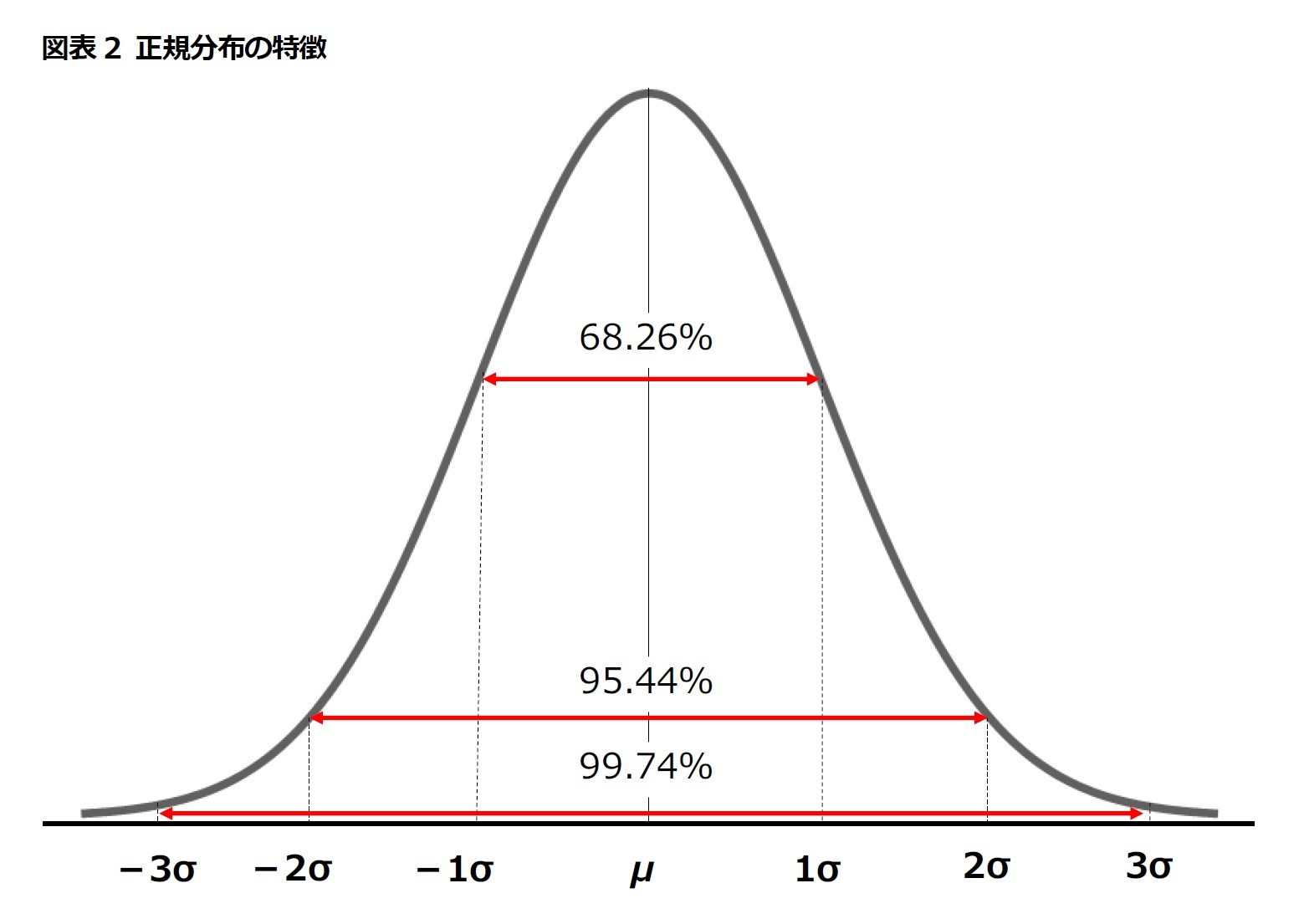
ここからですね。よく見る下記図。何で、標準偏差1までに68%、標準偏差2までに95%、標準偏差3までに99.74%って言えるの?そもそもこの図と確率って関係あるの??って事が解き明かしたい課題です。
正規分布と確率の関係
正規分布では、曲線の下の面積が「確率」を表している。
これが確率と正規分布のつながり。
• 縦軸は「確率密度」 (Probability Density Function: PDF)。
• 横軸は「データの値」。
\begin{align}
P(a \leq X \leq b) = \int_a^b f(x) \, dx \\
•f(x) :正規分布の確率密度関数 \\
•a から b までの面積が、その範囲にデータが存在する確率になる。\\
\end{align}
なぜ正規分布が確率に使われるのか?
理由1: 正規分布は「積み重なった要因」の結果だから
中心極限定理という数学的法則がポイントだよ。
• 中心極限定理とは:
無数の小さな独立した要因が組み合わさってできるデータは、どんな分布の要因でも、正規分布に近づくというもの。
例:テストの点数
テストの点数は「たくさんの小さな要因」が積み重なって決まるよね?
• 勉強量、睡眠時間、体調、試験中の集中力、問題の難しさ……など。
これらの要因が無数に組み合わさると、全体の分布は自然と正規分布に近づくんだ。
理由2: 正規分布は確率のルールに従っている
正規分布は次の確率の基本ルールを満たしているから、確率計算に使えるんだ。
- 確率の合計は1になる
• 正規分布の曲線の下の面積全体は「1」になる。
→ 「すべてのデータがどこかに存在する確率が100%」という意味だよ。
数式で表すと:
\int_{-\infty}^{\infty} f(x) \, dx = 1
- 確率は部分的な面積で表せる
• a から b の範囲にデータが存在する確率は、曲線の下の「その範囲の面積」になる。
理由3: 正規分布の左右対称性と標準偏差
正規分布は平均を中心に左右対称で、標準偏差によって「確率の範囲」が決まるよ。
例えば:
• 平均 ±1標準偏差 → 約68% のデータが含まれる。
• 平均 ±2標準偏差 → 約95% のデータが含まれる。
• 平均 ±3標準偏差 → 約99.7% のデータが含まれる。
このように、正規分布の形が「確率の範囲」として非常に使いやすいんだ。
具体例:正規分布と確率の関係
問題:
「テストの点数が平均70点、標準偏差10点の正規分布に従うとき、80点以上を取る確率は?」
ステップ1:標準化する
z = \frac{x - \mu}{\sigma} = \frac{80 - 70}{10} = 1
→ 80点は「平均から1標準偏差上」に位置する。
ステップ2:標準正規分布を使う
標準正規分布表を見れば、 z = 1 以下の確率は 0.8413。
80点以上の確率は:
P(X \geq 80) = 1 - 0.8413 = 0.1587
→ 約15.87%の確率で80点以上を取れる。
結論
正規分布が確率に利用される理由は:
1. 自然現象やデータが正規分布に従いやすい(中心極限定理)。
2. 曲線の下の面積が確率を表すという確率のルールに適合している。
3. 計算が便利(標準化すればどんな正規分布も標準正規分布で確率計算できる)。