はじめに
Rを学びたい Step14です!今回は共分散、相関係数を学んでいきます!!
共分散とは?
2つの変数がどのように一緒に変動するかを測る指標です。
\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^n \left( X_i - \bar{X} \right) \left( Y_i - \bar{Y} \right)
\begin{align*}
&\bullet \ X \text{ と } Y: \text{2つの変数} \\
&\bullet \ X_i, Y_i: X \text{ と } Y \text{ のそれぞれのデータ点} \\
&\bullet \ \bar{X}, \bar{Y}: X \text{ と } Y \text{ の平均値} \\
&\bullet \ n: \text{データの個数}
\end{align*}
→共分散だけだと結局何を示しているのかよくわからんですね。相関係数のための値なので、相関係数も一緒に学びます。
相関係数
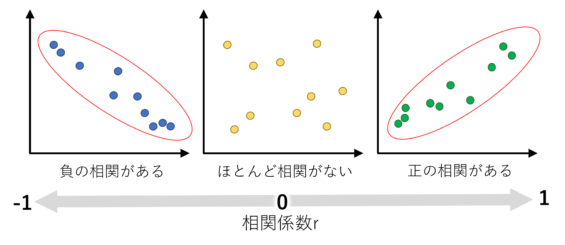
2つの変数の間にどのような関係があるか(強さと方向性)を示す指標です。値は -1から1の間をとり、次のように解釈します。
-
相関係数の範囲と意味
• r = 1
→ 完全な正の相関。
例: X が増えると Y も比例して増える。
• r = -1
→ 完全な負の相関。
例: X が増えると Y は比例して減る。
• r = 0
→ 相関なし。
例: X と Y は独立しており、関係がない。
r = \frac{\text{Cov}(X, Y)}{\sigma_X \cdot \sigma_Y}
\begin{align*}
&\bullet \text{Cov}(X, Y): X と Y の共分散(2つの変数がどれだけ一緒に動くか)。 \\
&\bullet \sigma_X, \sigma_Y: X と Y の標準偏差(それぞれの変数のばらつき)。 \\
\end{align*}
結局なんなの??共分散と相関係数
共分散、相関係数は公式としては理解できるのですが、結局なんなの??🤔という感じでした。
そもそも相関係数がなぜ必要なのかという事を想像してみるといいかもしれません。
例えば、上記のような散布図があった場合、これはHeightに対してWeightは相関関係があるのか?と言われた時に、どうでしょうか??
なんとなく、左下から右下に伸びているので相関関係がありそうですね。ただ、これがどれくらい相関関係があるのかは判定できないです。言葉で伝える事はできないので、この図を見てください!!って言うしかないですが、毎回この図を見てくださいはちょっと辛いですね。😅
そこで評価しやすい指標が必要であり、それが 相関係数です!
相関関係は向きと大きさを示しております。
次にどうやって相関関係を示すのか??
Xが大きくなるとYも大きくなり、Xが小さくなればYも小さくなります。第1象限、第3象限にあれば正の相関があり、第2象限、第4象限にあれば負の相関があると言えます。
第1象限~第4象限の値の総和を点の総数で割った物が共分散、共分散を標準化して-1~1の間に収めたものが相関係数です!!
ソースコード
では実際にRで共分散、相関係数を算出したいと思います。
問題
ある夏、アイスクリーム屋さんの店長さんが、売上と気温の関係を示してください。次のようなデータを1週間分集めました:
• 気温(°C): 25, 27, 30, 32, 35, 37, 40
• 売上(個数): 100, 120, 140, 150, 170, 180, 200
# 気温(X)と売上(Y)のデータ
temperature <- c(25, 27, 30, 32, 35, 37, 40) # 気温
sales <- c(100, 120, 140, 150, 170, 180, 200) # 売上個数
# 共分散の計算
covariance <- cov(temperature, sales)
print(paste("Covariance:", covariance))
# 相関係数の計算
correlation <- cor(temperature, sales)
print(paste("Correlation coefficient:", correlation))
# プロットして可視化
plot(temperature, sales, main = "Relationship between Temperature and Ice Cream Sales",
xlab = "Temperature (°C)", ylab = "Sales (Units)", pch = 16, col = "blue")
abline(lm(sales ~ temperature), col = "red") # 回帰直線
[1] "Covariance: 187.857142857143"
[1] "Correlation coefficient: 0.996994429431045"