混合ガウス分布のEMアルゴリズムによる推定

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
plt.style.use("ggplot")

K = 2
M = 1
N = 1000

# 実際の値
mu1 = 1
sigma1 = 0.2
N1 = int(N*0.3)
mu2 = 5
sigma2 = 1
N2 = int(N*0.7)

x = np.concatenate([np.random.normal(mu1, sigma1, N1), np.random.normal(mu2, sigma2, N2)])
plt.hist(x, bins=100, normed=True)
plt.show()

# 初期値
w = np.random.uniform(0,1,K)
w /=  w.sum()
mu = [3, 10]
sigma = [1, 1]
ita = np.zeros([N, K])

# EM アルゴリズム
training_iter = 50
for epoch in range(training_iter):
    # Estep
    for k in range(K):
        ita[:, k] = w[k] * stats.norm(mu[k], sigma[k]).pdf(x)
    ita = ita/ita.sum(1)[:, np.newaxis]

    # Mstep
    w = ita.sum(0) / N 
    mu = ita.T.dot(x) / ita.sum(0)
    for k in range(K):
        sigma[k] = np.sqrt(((x - mu[k]) ** 2 * ita[:, k]).sum(0) / ita[:, k].sum() * M)
    # 図示    
    x_ = np.linspace(0, 8, 200)
    y0 = w[0] * stats.norm(mu[0], sigma[0]).pdf(x_) 
    y1 = w[1] * stats.norm(mu[1], sigma[1]).pdf(x_) 
    plt.plot(x_, y0)
    plt.plot(x_, y1)
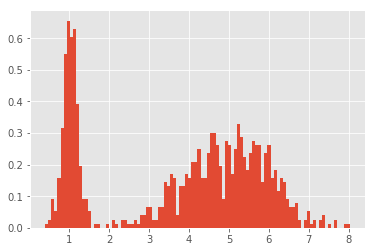
    plt.hist(x, bins=100, normed=True)
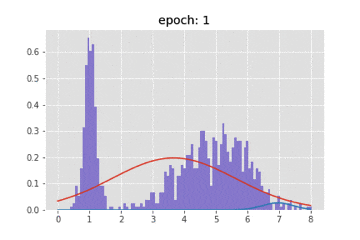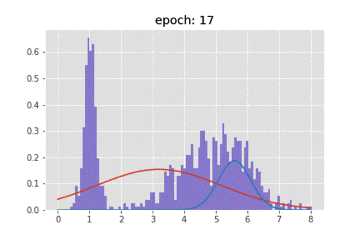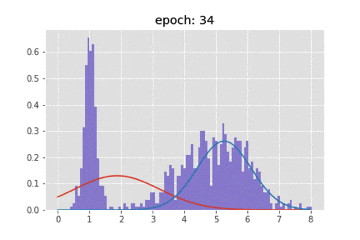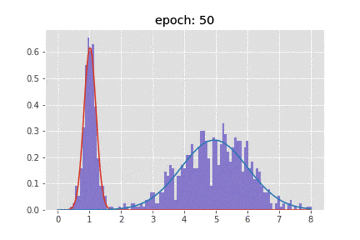
    title = "epoch: {}".format(epoch+1)
    plt.title(title)
    # plt.savefig("data/" + title + ".png")
    plt.show()