この記事では、ICLR 2023で発表された「TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis」を解説します。
少しでも分かりやすいなど思っていただけたら、「いいね」や「コメント」お願いします!間違いや指摘がございましたら遠慮なくお申し付けください!
TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis
忙しい方へのまとめ
この論文のやったことは大きく分けて3つです。
- 通常一つの次元方向に進行する時系列データを二次元に変換することで、複雑に絡み合った依存関係を捉えやすくした
- その二次元データに対してInception Blockで処理を施すTimes BlockというブロックをスタッキングしたTimesNetというモデルを提案した
- TimesNetは時系列の短期予測、長期予測、異常検知、欠損補完、分類の5つのタスク全てでSoTAを達成した
導入
時系列解析は気象予測やカードの不正利用検知など、実社会でも用いられている重要なタスクです。それらのタスクをより高精度に実行するために、これまでに様々な深層学習モデルが提案されてきました。
- LSTM(Hochreiter et al., 1997)などの再帰的ニューラルネットワーク(RNN)
- 畳み込みを用いたTemporal Convolutional Network(Bai et al., 2018)
- Autoformer(Wu et al., 2021), FEDformer(Zhou et al., 2022)などのTransformer-basedモデル
どれも素晴らしいモデルですが、これらは長期の依存関係を捉えきれないことや計算コストがかかってしまうことなど、様々な問題を抱えています。
まず、著者は実世界の時系列データを調査し、多くの時系列データには周期性が複数あることを発見しました。 例えば、気温データでは一日や一年での周期性があります。このように複数の季節変動があることで各ステップの依存関係が複雑に絡み合い、予測などが難しくなっています。
そして著者は、この依存関係を捉えやすくするために下図のように、一次元方向に進行する時系列を二次元方向に変換する手法を考えました。
Intraperiod-variationは着目した周期性、Interperiod-variationはIntraperiod-variationを除いた変動を表しています。論文の図だと分かりにくいので自作の図で説明すると、例えば一時間ごとの気温データのとき、一日の周期性と一年の周期性を捉えやすくするために下図のようにするということです。
左下の変換では、縦に見れば一日の変動、横に見れば一日の変動を除いた変動を見ることができます。また右下の変換では、縦に見れば一年の変動、横に見れば一年の変動を除いた変動を見ることができます。
この変換を次章で紹介するTimesNetというモデルに組み込むことで、複雑な依存関係をより効果的に捉えることを可能にし、時系列の短期予測、長期予測、異常検知、欠損補完、分類の5つのタスク全てでSoTAを達成できたとのことです。
TimesNet
この章では、前章で説明した二次元への変換の詳しい説明と、それを用いたモデルの説明をします。
一次元方向に進行する時系列の二次元への変換
前章で二次元に変換することで、時系列の依存関係が捉えやすくなったのは理解できたとして、気になるのはどのように変換したかですよね。もちろんテキトーに周期を決めて、そこで折り返すように変換しても意味がないわけで、先ほど例に出した気温のデータの場合には、一日と一年の周期で折り返すようにしなくてはいけません。著者は高速フーリエ変換(FFT)を用いて重要な周期を算出し、その周期で変換するようにしています。
元の時系列を$X_{1D}\in\mathbb{R}^{L\times F}$(Lを時系列の長さ、Fを特徴量の数)としたとき、以下のようにして重要な周期$p$を算出します。
\mathbf{A}=Avg(Amp(FFT(X_{1D}))
f_1, f_2, \cdots, f_k = argTopk(\mathbf{A})
p_i=\lceil L/f_i\rceil, i\in\{1,\cdots, k\}
ここで、FFTは高速フーリエ変換、Ampは振幅、Avgは特徴量方向に平均をとる処理を表します。また、kはハイパーパラメータです。要するに、振幅が大きい上位k個の周期を選択するようにしているわけです。
この処理を
\mathbf{A}, \{f_1,\cdots,f_k\}, \{p_1,\cdots,p_k\}=Period(X_{1D})
とし、この周期$p_i$を用いて
X^i_{2D}=Reshape_{p_i}(X_{1D})
として、周期$p_i$それぞれに基づいて二次元に変換します。
気温データに例えるならば、FFTした際に一日の周期性を表す周波数ビンと一年の周期性を表す周波数ビンの振幅が大きく出るはずなので、k=2などと設定して、その二つの周波数ビンに対応する周期を算出するようにし、二次元データへの変換を行うことで、前章で紹介したような図にするということです。
TimesNet
次にTimesNetの具体的なモデル内部の構造について説明します。
TimesNetはTimes Blockと呼ばれるブロックをスタッキングして構成されています。
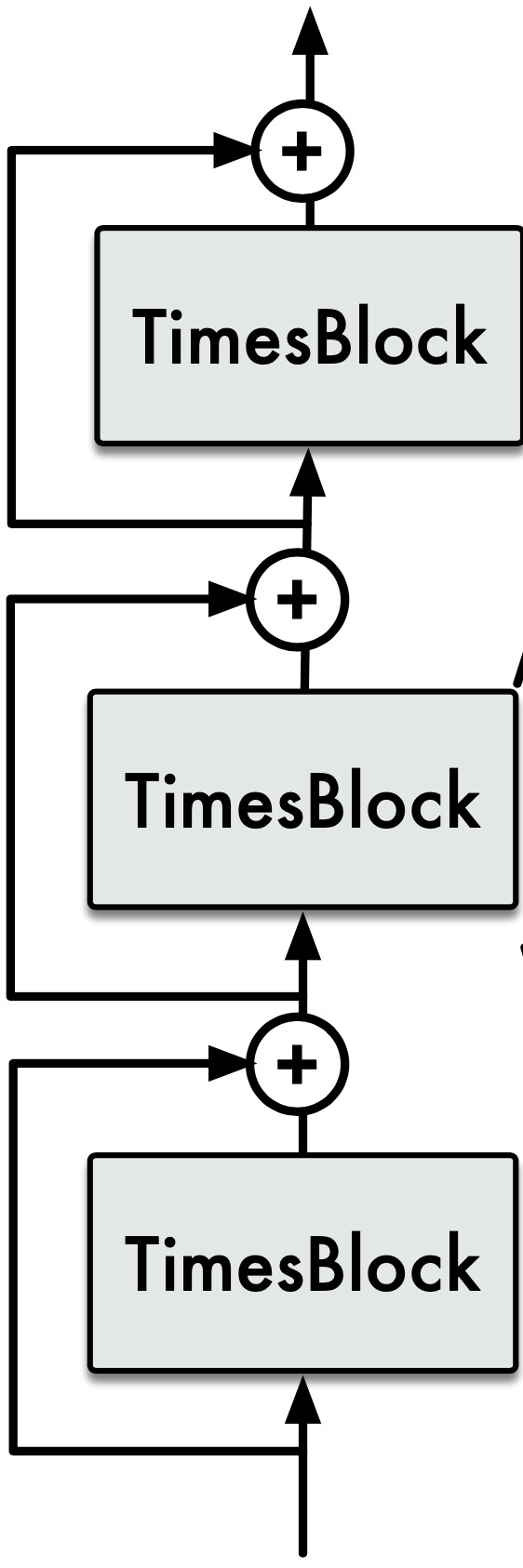
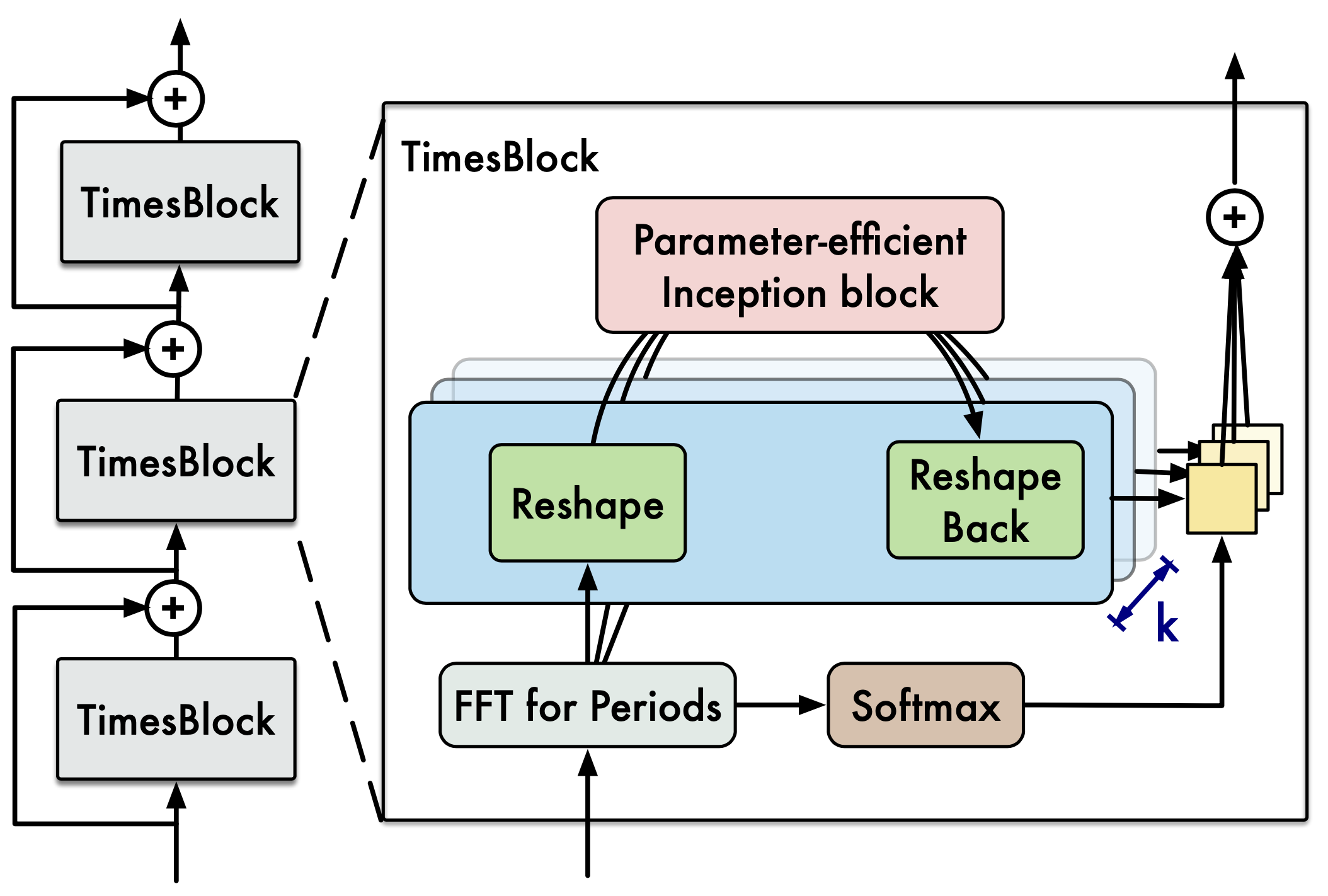
そして、一つ一つのTimes Blockは下図のような処理がされています。
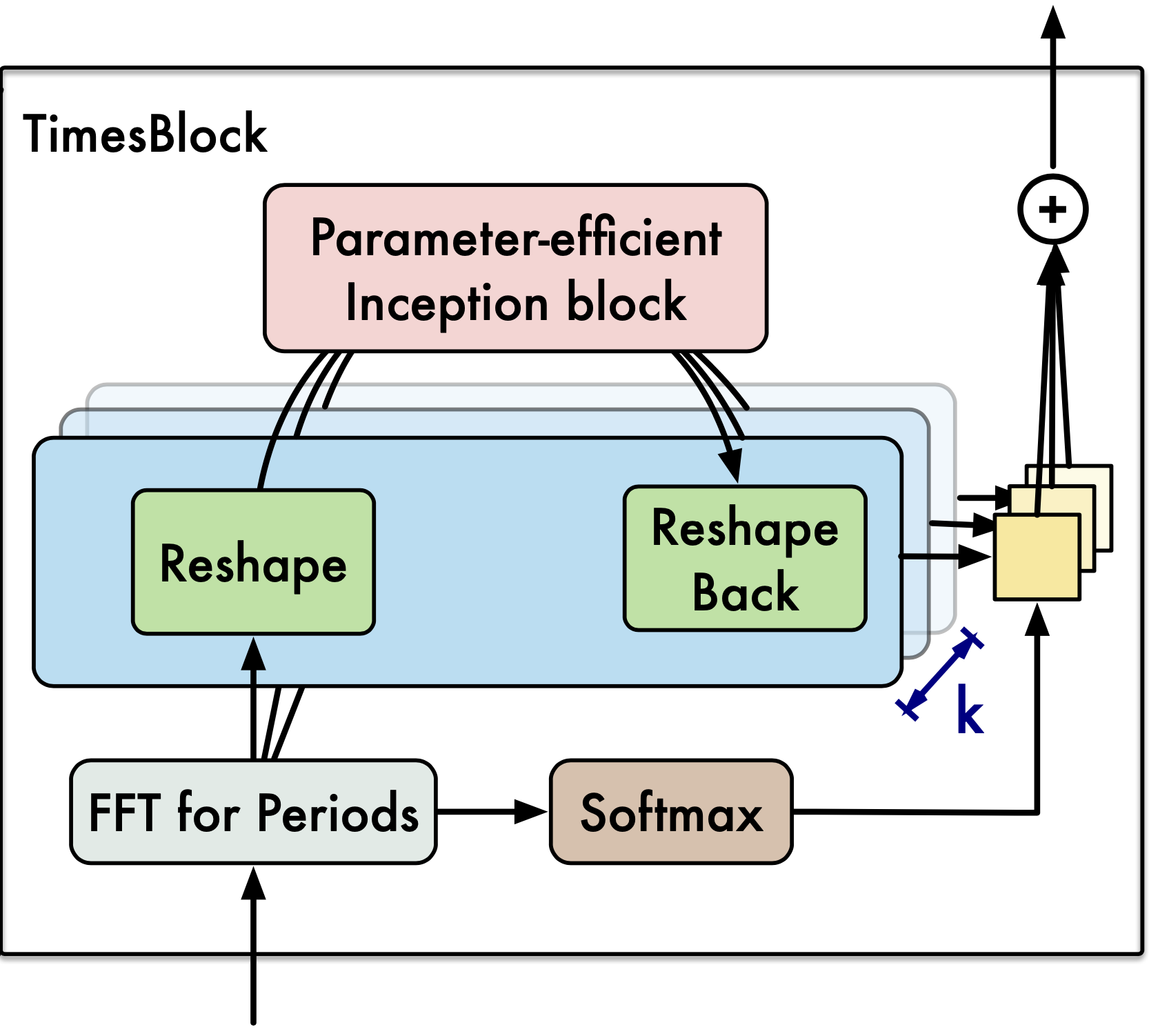
この処理を式で表すと、以下のようになります。
\mathbf{A}^{l-1}, \{f_1,\cdots,f_k\}, \{p_1,\cdots,p_k\}=Period(X_{1D}^{l-1}) \\
X^{l,i}_{2D}=Reshape_{p_i}(X_{1D}^{l-1}), i\in\{1,\cdots,k\} \\
X'^{l,i}_{2D}=Inception(X^{l,i}_{2D}), i\in\{1,\cdots,k\} \\
X'^{l,i}_{1D}=BackReshape_{p_i}(X'^{l,i}_{2D}), i\in\{1,\cdots,k\}
ここで、$X_{1D}^{l-1}\in\mathbb{R}^{L\times F}$は$l-1$層目のTimesBlockの出力、InceptionをInception Block(複数のカーネルサイズでConv2dをし、結合する処理)を表しています。これは、前節で説明したように時系列の重要な周期をk個算出し、それぞれの周期に基づいて時系列を二次元に変換した後、Inception BlockによってConv2dの計算をし、元の一次元の時系列に戻すという処理です。
そして、各周期$p_i$の振幅に基づいて重みを計算し、その重みに基づいて$\hat{X}^{l,i}_{1D}$を結合し、l層目のTimes Blockの出力
を計算します。
\mathbf{A'}_{p_1}^{l-1}, \cdots, \mathbf{A'}_{p_k}^{l-1}=Softmax(\mathbf{A}_{p_1}^{l-1}, \cdots, \mathbf{A}_{p_k}^{l-1}) \\
X_{1D}^l=\sum_{i=1}^{k}\mathbf{A'}_{p_i}^{l-1}\times X'^{l,i}_{1D}
よくわからなかった方は、「時系列を二次元の画像にようなものに変換して、画像処理を施して、一次元に戻すという処理を何層も行っている」程度の理解で大丈夫です。
実験・評価
次に、このモデルの評価を行います。評価方法は以下のデータセットと評価関数を用いた時系列の短期予測、長期予測、補完、分類、異常検知です。
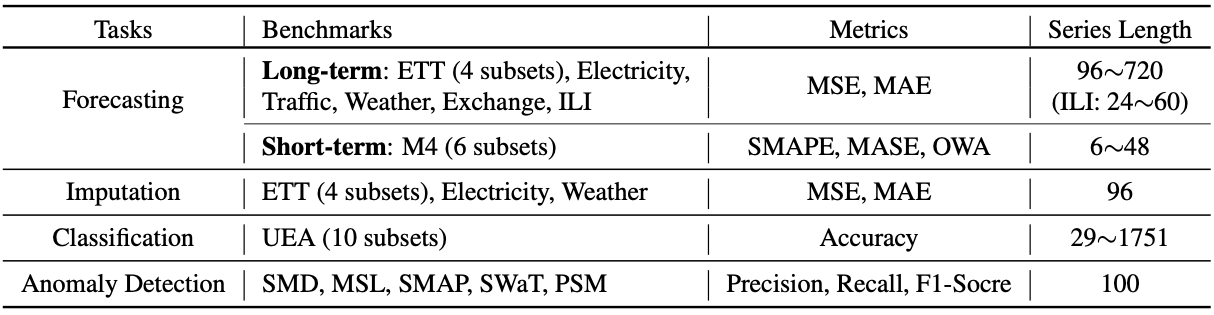
そして、その結果をまとめたものが以下になります。
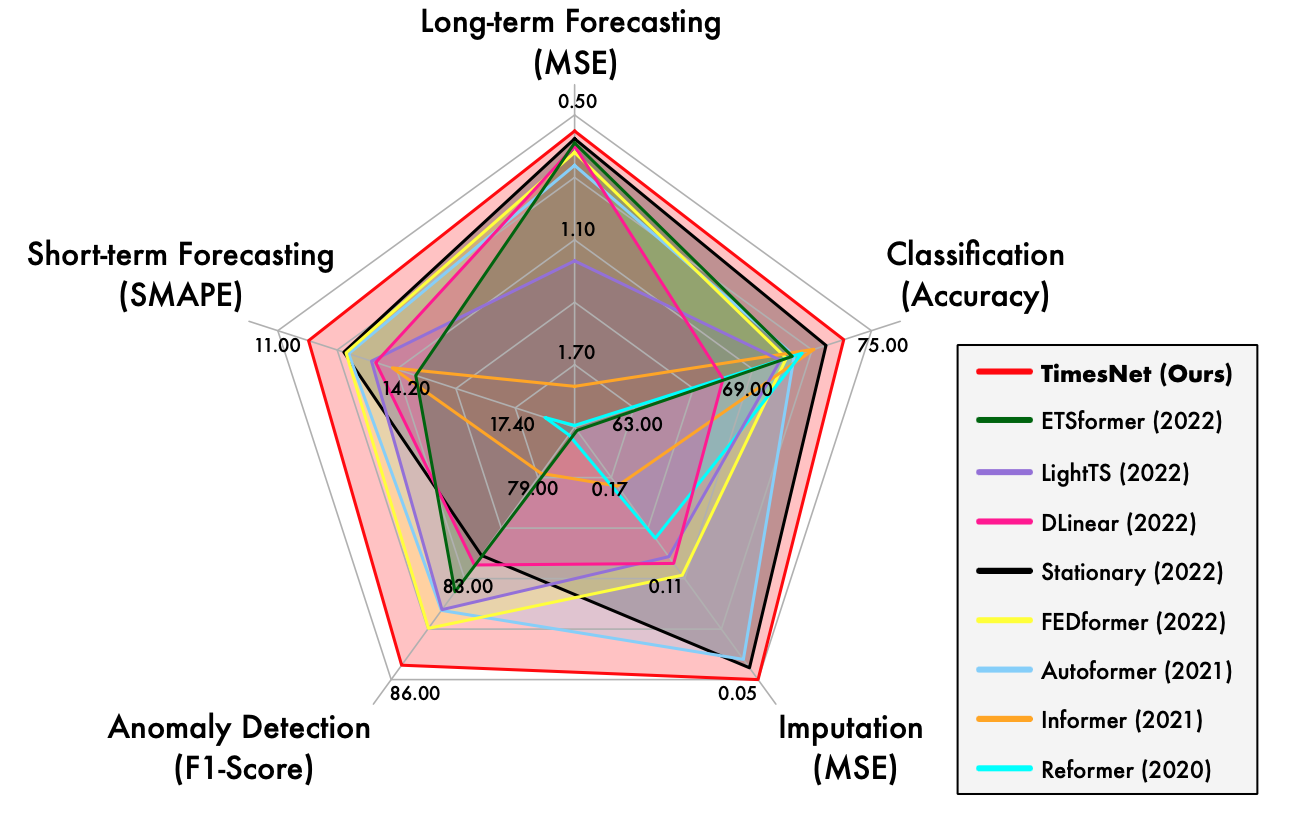
少しごちゃごちゃしていて見にくいですが、どのタスクでもTimesNetが最高精度を達成しています。二次元に変換して時系列の依存関係を捉えやすくすることでこんなに高精度を出すことができるんですね。細かい実験が気になる方はぜひ論文を読んでみてください。
結論・課題
今回は「TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis」の解説でした。時系列データを複数の季節変動が捉えやすいように二次元に変換し、それを用いてモデリングすることで様々なタスクでSoTAを達成することができるというのはすごいことですね。この論文では、単にInception Blockで二次元データを処理しましたが、他に効果的なものがあるかもしれないので、それを探してみるのもいいですね。
参考文献