この記事は富士通クラウドテクノロジーズ Advent Calender 2021の21日目の記事です。
20日目の記事は@thuydg@githubさんのニフクラmobile backendの新Kotlin SDKについてでした。
ものすごく丁寧な解説で、SDKをほとんど知らなかった私でも簡単に理解することできました!
ぜひご覧ください!!
はじめに
はじめまして!FJCT新人のコダックです。
FJCTではAI技術を使用して課題を解決するデータデザイン by ニフクラを提供しております。
そこで今回はAI関連の記事を書いていこうと思います。
テーマの背景
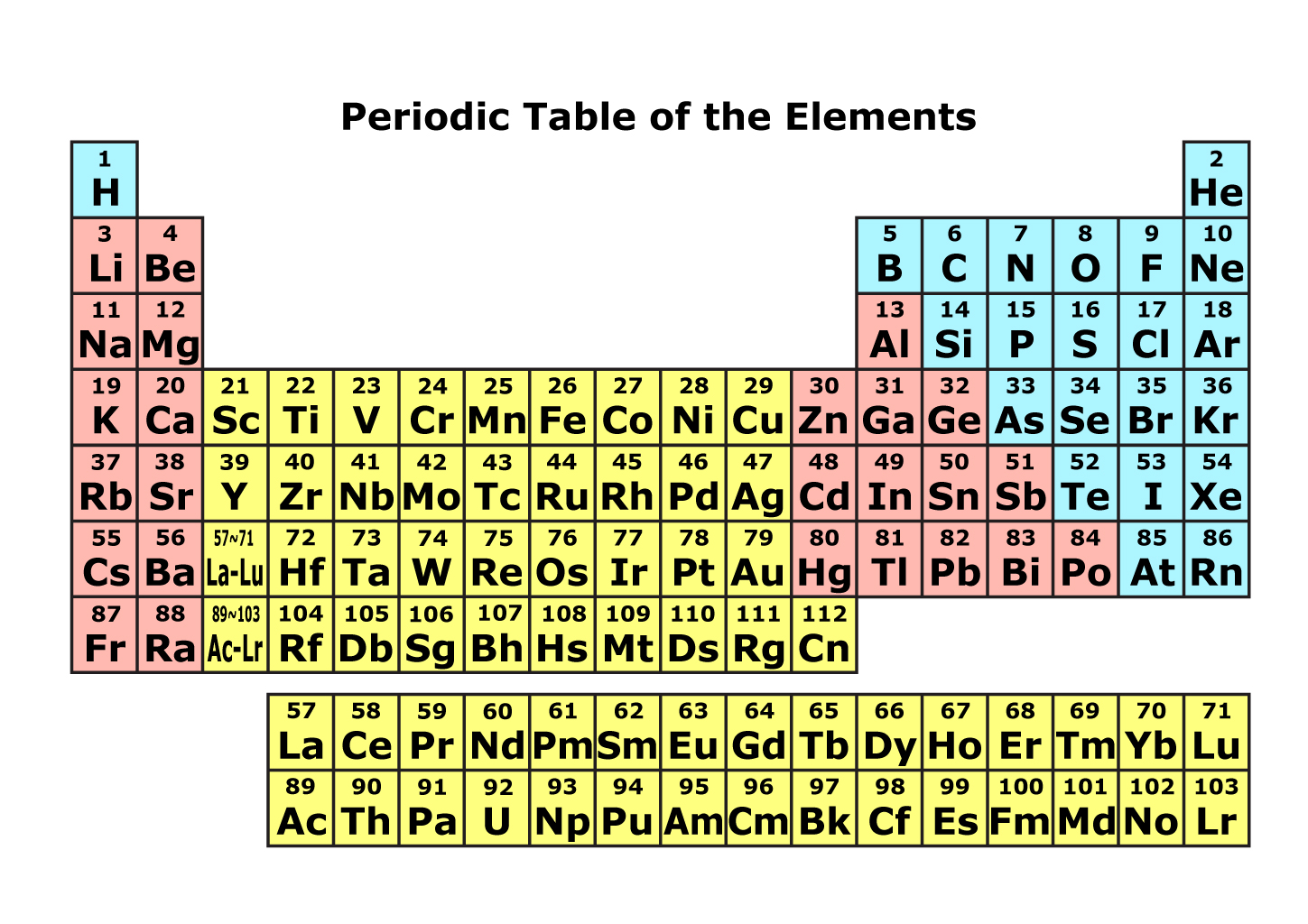
私は最近、化学系のYoutuberにハマっています。学生の頃は工学系の学校に通っていたため、化学についてほとんど学習しておらず、Youtubeを通して化学の面白さに触れ、少し学生時代に使っていた化学の教科書を見返してみました。まず目に入ったのが周期表で、その中に「族は性質が類似している」という記載がありました。
皆さんは、この「性質が類似」が本当に類似しているのかなと疑問に思ったことありませんか?
例えば11族には「金」「銀」「銅」が属していますが、「金」と「銅」の性質が似ているのか疑問でした。
そこで今回は、教師なし学習を使用して、周期表の族がどのくらい性質が似ているのかを分析してみることにしました!
教師なし学習について
教師なし学習とは、その名の通り教師データがない機械学習の手法になります。教師なし学習では、予測や判定の対象となる正解が存在しないため、回帰や分類には適用できません。
教師なし学習の代表例は、主成分分析とクラスタリングが挙げられます。クラスタリングではデータの特徴を捉えることにより、データのグループ化が可能となります。また、主成分分析では、次元の多いデータの次元を削減するために、使用される手法です。
今回は主成分分析を使用して、データの次元を削除することにより、元素の特徴を視覚的に捉えやすいように分析していきます!
今回使用する環境について
今回、私はR言語とPythonの両方で分析してみましたが、基本的にはR言語の方で記事を書こうと思います。理由としてはR言語の方が主成分分析のライブラリが豊富で、pythonより分析しやすかったからです。最後に軽くpythonで分析した結果も記載しております。
R:3.6.3
ggbiplot:0.55
python:3.7.4
numpy:1.17.2
pandas:0.25.1
matplotlib:3.1.1
sklearn:0.0
今回使用するデータについて
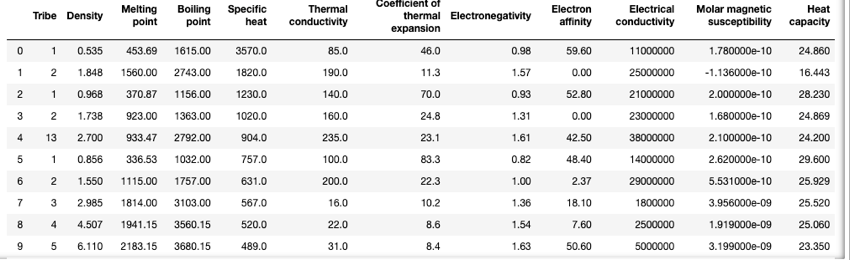
今回使用するデータは金属のみとしました。
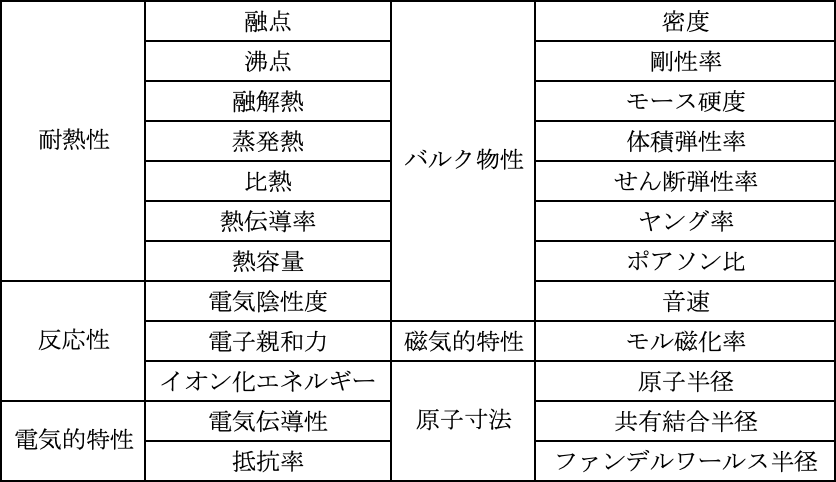
主成分分析の対象のデータとして、金属元素の熱特性(Thermal properties)、バルク物性 (Bulk physical properties)、反応性(Reactivity)、電気的特性(Electrical properties)、磁気的特性 (Magnetic properties)、原子寸法等のデータを使用します。
値についてはElement Collection,incのTheodore Gray によるウェブサイトから抽出しています。(正直なところ、データを作るのが一番大変でした、、)
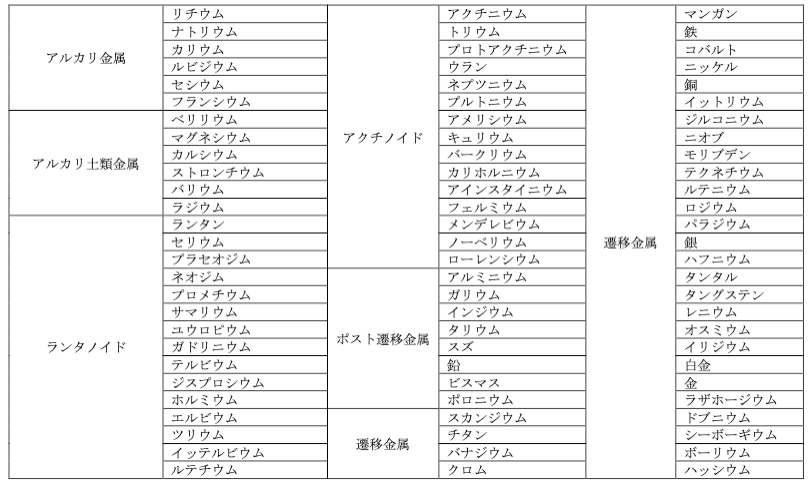
金属元素として、一般的に金属に分類されるアルカリ金属、アルカリ土類金属、ランタノイド、アクチノイド、遷移金属、ポスト遷移金属、半金属を対象としました。
パラメータ(調査項目)としては、下記に示すような項目をまとめました。しかし、元素によって調査できないものがあり、データの欠損部ができたため、分析前にまとめたデータから欠損の多い項目・元素を削除しています。削除する際には各元素の特徴が失われないよう注意しながら行いました。
以下に今回使用したデータの一部を記載しています。
主成分分析(R言語)
正規化
まずはデータの正規化を行います。Rではscaleを使用して正規化できます。
> data <- scale(data_ori)
主成分の数
次に関数prcompを使用して主成分分析を行い、関数summaryを使用して出力結果を確認します。
> pca<-prcomp(data[,-12],scale=T)
> summary(pca)
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11
Standard deviation 1.9889 1.4962 1.2778 1.00646 0.86480 0.77587 0.61634 0.4260 0.35429 0.27385 0.21952
Proportion of Variance 0.3596 0.2035 0.1484 0.09209 0.06799 0.05472 0.03453 0.0165 0.01141 0.00682 0.00438
Cumulative Proportion 0.3596 0.5631 0.7116 0.80364 0.87163 0.92636 0.96089 0.9774 0.98880 0.99562 1.00000
この出力結果で確認する箇所は、累積寄与率(Cumulative Proportion)です。第1主成分のみで36%、第2主成分までで56%、第3主成分までで71%となっています。主成分の選択として、累積寄与率を用いたものでは、累積寄与率が70~80%になる前後までが採用されます。そのため、今回は第3主成分までを用いて分析を行うことに決めました。
主成分係数
次に、関数prcompを使用して計算された主成分係数を出力してみます。値は小数点以下3桁までとしています。
> round(pca$rotation, 3)
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11
Density 0.415 -0.138 0.287 -0.001 -0.190 0.086 -0.207 0.653 -0.151 0.433 0.053
Melting.point 0.428 -0.141 -0.266 0.078 0.152 -0.049 -0.411 -0.032 -0.049 -0.287 -0.664
Boiling.point 0.438 -0.149 -0.210 0.103 0.097 -0.101 -0.365 -0.295 0.245 0.012 0.657
Specific.heat -0.220 0.261 -0.392 0.154 -0.581 -0.374 -0.205 0.310 0.284 -0.095 0.006
Thermal.conductivity 0.117 0.605 0.173 -0.002 0.149 0.003 -0.162 0.192 -0.421 -0.513 0.256
Coefficient.of.thermal.expansion -0.324 -0.095 0.387 -0.029 -0.379 0.264 -0.623 -0.343 -0.120 -0.014 -0.036
Electronegativity 0.383 0.069 0.283 -0.167 -0.380 0.334 0.285 -0.041 0.499 -0.387 -0.056
Electron.affinity 0.295 0.216 0.372 0.088 -0.210 -0.631 0.153 -0.401 -0.141 0.221 -0.156
Electrical.conductivity -0.023 0.606 0.061 -0.060 0.336 0.167 -0.240 -0.041 0.465 0.421 -0.176
Molar.magnetic.susceptibility 0.023 -0.007 -0.151 -0.959 -0.043 -0.198 -0.103 -0.009 -0.066 0.032 0.024
Heat.capacity -0.227 -0.278 0.474 -0.025 0.352 -0.439 -0.160 0.264 0.392 -0.284 0.013
ここから今回採択した第1~3主成分の意味づけを行うために、因子負荷量をプロットしていきます。コマンドは次のようになります。
> fc.l <- sweep(pca$rotation, MARGIN=2, pca$sdev, FUN="*")
# PC1の図を作成
> plot(fc.l[,1], ylim=c(-1,1), main="PC1", type="n")
> text(fc.l[,1], colnames(data))
> abline(h=0, lty=2)
# PC2の図を作成
> plot(fc.l[,2], ylim=c(-1,1), main="PC2", type="n")
> text(fc.l[,2], colnames(data))
> abline(h=0, lty=2)
# PC3の図を作成
> plot(fc.l[,3], ylim=c(-1,1), main="PC3", type="n")
> text(fc.l[,3], colnames(data))
> abline(h=0, lty=2)
作成された図が以下になります。
| 第1主成分 | 第2主成分 | 第3主成分 |
|---|---|---|
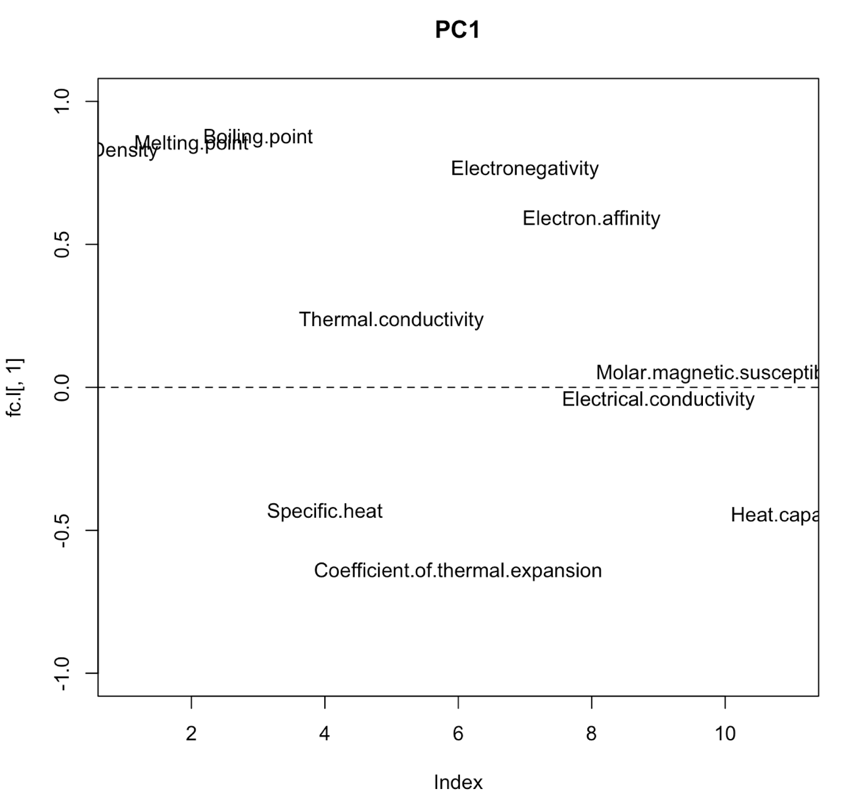 |
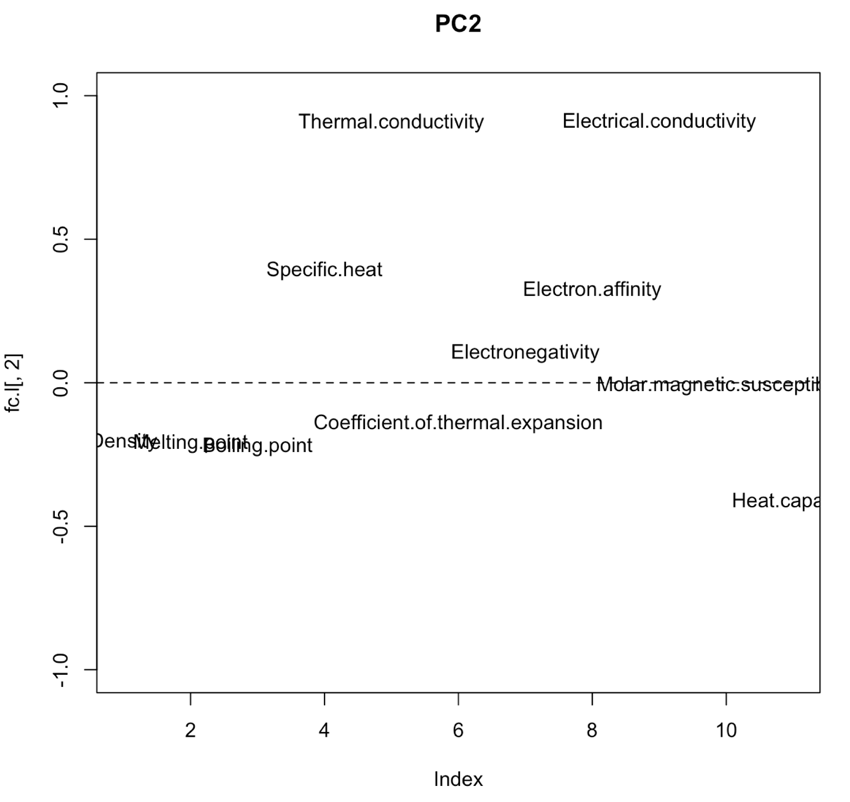 |
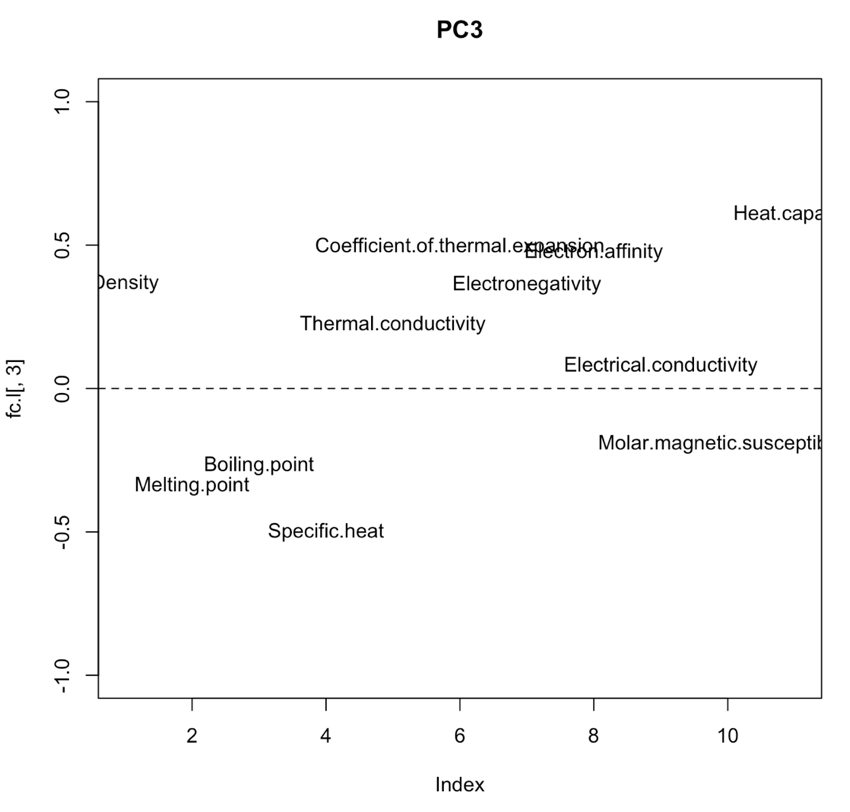 |
第1主成分(PC1)は、密度・融点・沸点・電気陰性度・電子親和力・熱膨張率・比熱・熱容量と強い相関があることがグラフから見て取れます。よって、第1主成分は物体の変化のしやすさの因子となっていると考えられます。
また、第2主成分(PC2)は、熱伝導率・電気伝導性と強い相関があることがグラフから見て取れます。よって、結晶格子の完全性・つまり結晶性の良さの因子となっていると考えられます。
第3主成分(PC3)は熱容量・比熱・熱膨張率と相関があることから、熱による変化のしやすさとなっていると考えられます。
主成分得点
次に、関数prcompを使用して計算された主成分得点の出力を行います。値は小数点以下3桁までを出力しました。
> round(pca$x,3)
PC1 PC2 PC3 PC4 PC5 PC6 PC7 PC8 PC9 PC10 PC11
Li -3.322 1.650 -2.286 1.086 -2.929 -2.157 -0.589 0.799 0.590 -0.029 0.090
Be -0.275 2.892 -3.586 0.553 -1.750 1.598 0.248 -0.398 -0.770 0.306 0.022
Na -3.206 0.912 0.461 0.337 0.018 -0.975 -0.638 0.023 -0.016 -0.031 -0.041
Mg -1.949 1.323 -0.880 0.187 0.212 0.386 0.198 0.351 -0.066 -0.213 -0.161
Al -0.777 2.544 -0.463 0.163 0.380 0.405 -0.163 -0.204 0.374 -0.041 0.331
K -3.510 -0.087 1.051 0.238 0.428 -0.962 -0.654 -0.188 -0.225 -0.072 -0.074
Ca -1.906 1.436 -0.604 0.206 1.313 0.182 -0.230 0.266 -0.295 -0.118 -0.051
Sc -0.715 -1.023 -1.232 0.376 0.286 -0.157 0.410 -0.278 0.014 -0.242 -0.121
Ti -0.242 -1.025 -1.301 0.329 0.198 0.197 0.329 -0.212 0.164 -0.304 0.026
V 0.515 -0.546 -1.299 0.394 -0.218 0.165 0.403 -0.619 -0.164 0.099 -0.225
Cr 0.416 -0.122 -0.573 0.313 0.125 -0.187 0.415 -0.141 -0.218 -0.243 -0.448
Mn -0.890 -1.323 -0.501 0.163 0.021 0.281 0.445 0.397 0.103 -0.174 -0.215
Fe 0.247 -0.351 -1.381 -4.864 -0.126 -0.487 -0.221 0.123 -0.068 -0.142 0.067
Co 0.634 0.296 -0.768 -3.759 -0.166 -0.601 -0.120 -0.173 0.001 0.206 -0.074
Ni 0.651 0.181 0.450 0.229 -0.118 -0.636 0.433 -0.334 0.355 0.041 -0.270
Cu 0.877 4.407 1.109 -0.012 1.129 0.284 -0.535 -0.078 0.138 0.160 0.030
Zn -1.388 0.416 0.177 -0.116 0.179 0.971 0.623 0.553 -0.095 -0.011 -0.118
Ga -1.921 -0.808 1.221 -0.103 -1.280 1.150 -0.619 -1.047 0.081 0.107 0.420
Sr -2.014 -0.754 -0.598 0.220 0.916 -0.010 0.493 0.005 -0.477 0.235 -0.207
Y -0.530 -1.327 -0.831 0.397 0.772 -0.440 0.194 -0.320 -0.062 -0.066 0.125
Zr 0.407 -1.246 -1.125 0.488 0.602 -0.334 -0.018 -0.527 -0.074 0.090 0.359
Nb 1.483 -0.723 -0.847 0.522 0.290 -0.459 -0.236 -0.826 -0.066 0.081 -0.038
Mo 2.178 0.450 -0.479 0.248 0.264 0.396 -0.313 -0.497 0.489 -0.333 -0.144
Ru 2.210 0.222 -0.043 0.245 -0.204 0.107 0.084 -0.433 0.203 -0.104 -0.215
Rh 1.934 0.830 0.548 0.116 0.009 0.050 0.117 -0.258 0.548 -0.031 -0.234
Pd 0.920 -0.473 0.381 0.013 -0.128 0.370 0.500 0.249 0.586 -0.224 -0.159
Ag 0.835 4.595 1.733 -0.115 1.377 0.240 -0.557 0.171 0.112 0.138 -0.036
Cd -1.370 -0.010 0.495 -0.183 0.205 0.989 0.770 0.678 -0.082 0.074 -0.130
In -1.009 -0.236 0.681 -0.088 0.153 0.452 0.672 0.114 0.321 0.000 0.460
Sn -0.196 -0.215 1.170 0.030 -0.157 -0.548 1.072 -0.475 0.457 0.099 0.412
Cs -3.800 -1.519 2.003 0.100 0.891 -1.147 -0.673 -0.222 -0.132 -0.188 -0.125
Ba -1.968 -1.364 -0.228 0.265 1.174 -0.534 0.405 0.093 -0.323 0.136 0.065
Hf 0.839 -1.705 -1.068 0.432 0.866 0.203 -0.585 0.403 -0.115 0.305 0.356
Ta 2.064 -1.373 -0.916 0.517 0.762 0.069 -1.144 0.306 -0.026 0.276 0.154
W 3.689 -0.587 -0.156 0.360 -0.250 0.289 -0.738 0.237 -0.183 -0.811 0.072
Re 2.689 -1.681 -0.651 0.378 0.361 0.538 -1.150 0.815 0.342 0.096 0.142
Os 3.442 -1.076 0.223 0.390 -0.505 -0.136 -0.457 0.401 -0.167 0.132 -0.148
Ir 3.277 -0.377 0.987 0.365 -0.634 -0.649 -0.119 0.364 -0.527 0.114 0.001
Pt 2.863 -0.238 1.721 0.284 -0.870 -1.211 0.467 -0.122 0.102 0.935 -0.272
Au 2.736 1.500 2.619 0.110 -1.121 -1.074 0.895 0.125 -1.096 -0.572 0.384
Hg -2.728 -1.809 3.011 -0.464 -1.952 1.953 -1.368 -0.161 -0.183 0.013 -0.273
Tl -0.941 -0.804 0.634 -0.075 0.037 0.616 0.747 0.647 -0.185 0.458 0.145
Pb -0.247 -0.852 1.139 -0.276 -0.561 0.814 1.208 0.391 0.635 -0.149 0.118
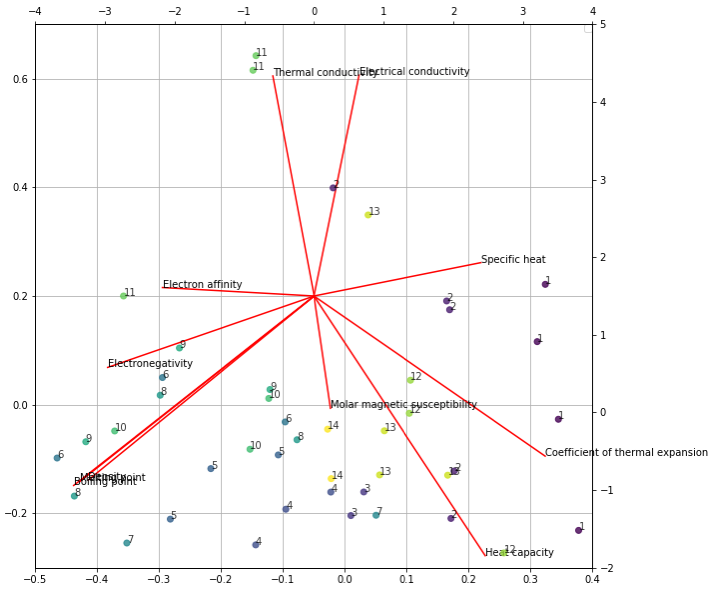
主成分得点をもとに、主成分得点散布図を作成していきます。今回は主成分と比較するためにバイプロットを使用します。バイプロットのコマンドは以下になります。
# 第1、2主成分のバイプロット
> biplot(pca$x,pca$rotation)
# 第1、3主成分のバイプロット
> biplot(pca$x[,-2],pca$rotation[,-2])
| 第1、2主成分のバイプロット | 第1、3主成分のバイプロット |
|---|---|
 |
 |
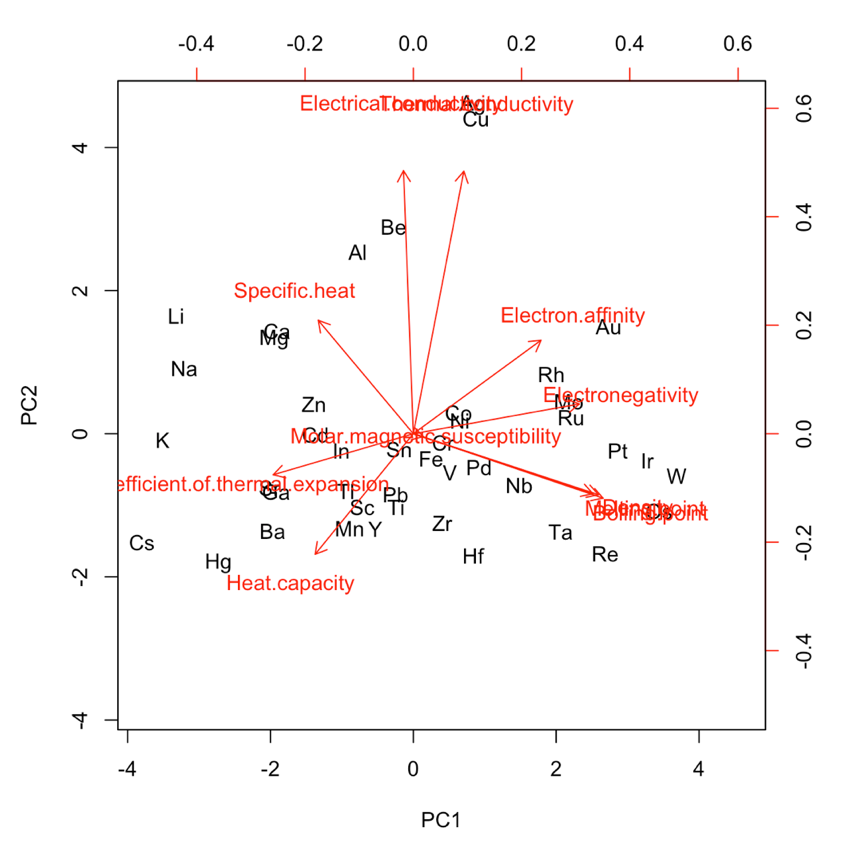
第1、2主成分のバイプロットでは上部に行くほど電気伝導性や熱伝導率が高く、結晶性の良い元素、右に行くほど加えたエネルギーに対する物体の状態の変化が小さく、状態変化しにくい元素となっています。具体的に元素を見てみると、上部には、銀(Ag)や銅(Cu)などが位置しています。これらは実際ケーブルなどの導線としてよく用いられている元素です。また、右のやや下部にはタングステン(W)が位置していますが,タングステンはフィラメントなどの材料として用いられており、融点の高さ(変化のしにくさ)、抵抗の高さが活かされています。
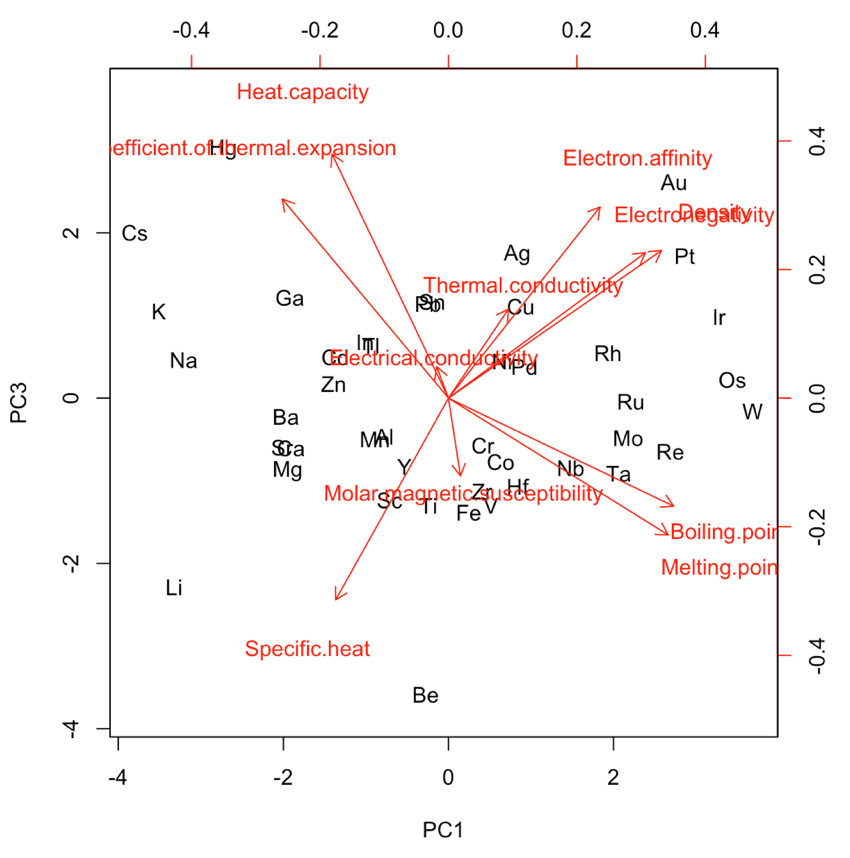
第1、3主成分のバイプロットでは上部に行くほど熱による変化が大きい元素で、右に行くほど加えたエネルギーに対する物体の状態の変化が小さい元素となっています。つまり、右上の領域は、加工しやすく耐久性が高いものとなっています。実際に、元素を見てみると、右上の領域には、金(Au)や銀(Ag)、プラチナ(Pt)等が位置しています。これらは投資などでも用いられるような価値の高いといわれる金属であり、特徴が表れているといえます。
族でグルーピング
最後に今回の一番の目的であった族についての分析を行っていきます。先ほどのバイプロットの図を、族ごとでグルーピングしてみます。
使用するライブラリはggbiplotです。インストール方法は以下になります。
> install.packages("devtools")
> devtools::install_github("vqv/ggbiplot")
コマンドは以下の通りになります。
# 第1、2主成分のggbiplotによるバイプロット
> ggbiplot(pca,choices=c(1,2),obs.scale=1,var.scale=1,groups=data$Tribe,
ellipse=TRUE,circle=TRUE,alpha=1)
# 第1、3主成分のggbiplotによるバイプロット
> ggbiplot(pca,choices=c(1,3),obs.scale=1,var.scale=1,groups=data$Tribe,
ellipse=TRUE,circle=TRUE,alpha=1)
| 第1、2主成分のggbiplotによるバイプロット | 第1、3主成分のggbiplotによるバイプロット |
|---|---|
 |
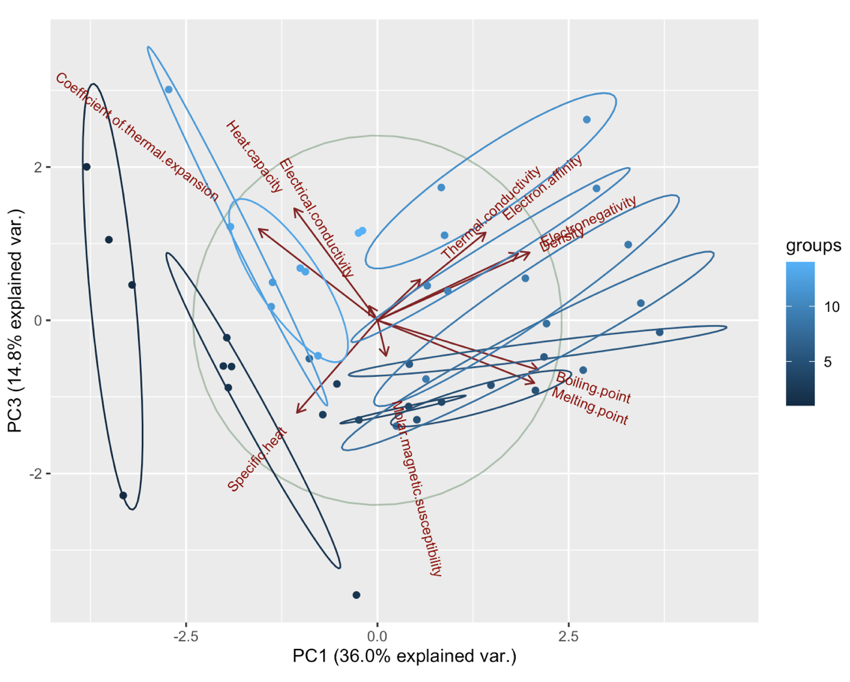 |
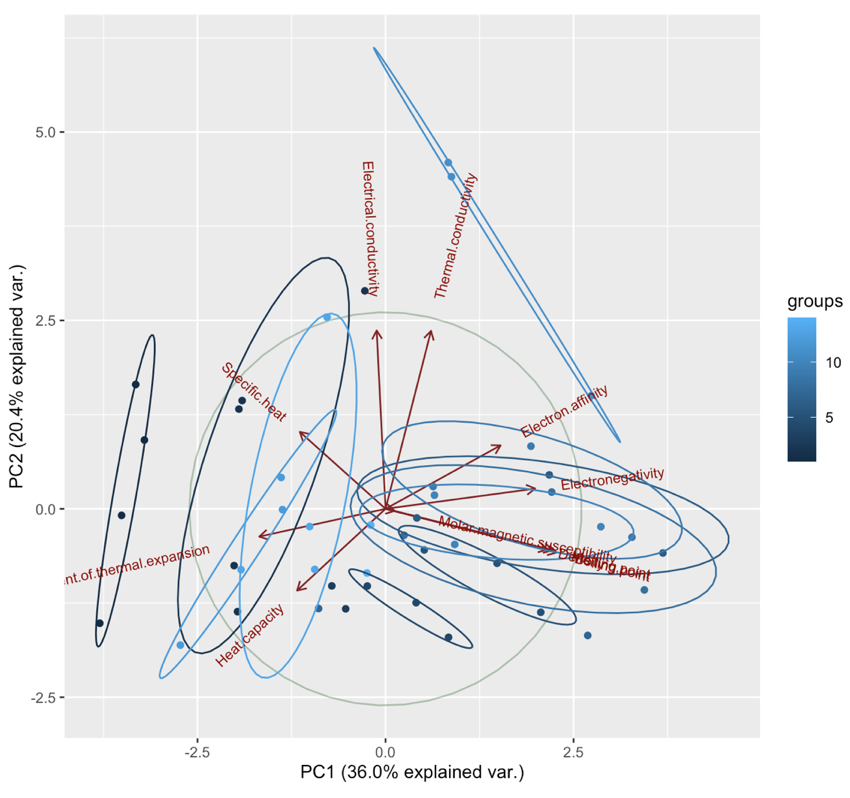
グラフを見ると、同族の元素を囲む円は全て伸びた楕円形になっていることが確認できます。このグルーピング結果は、短軸がその族で特有の特徴、長軸がその族の中での周期による違いが表れていると捉えることができます。それぞれの族ごとの特徴が表れた分析を行うことができたと言っていいでしょう。
pythonでの主成分分析について
少しだけpythonで主成分分析を行った結果も残しておきます。正直なところ、R言語を使用できるのであれば、pythonでの主成分分析はあまりお勧めしません(個人的な意見)
理由はライブラリ数の違いや、グラフを出力する上でのコードの長さ(面倒さ)などがあります。
使用したライブラリ
# 数値計算やデータフレーム操作に関するライブラリ
import numpy as np
import pandas as pd
# 図やグラフを図示するためのライブラリ
import matplotlib.pyplot as plt
%matplotlib inline
# 機械学習のライブラリ
import sklearn
# 主成分分析器
from sklearn.decomposition import PCA
バイプロットを出力する
fig, ax1 = plt.subplots(1,1,figsize=(10,10))
ax2 = ax1.twinx().twiny()
# 因子負荷量のプロット
for x, y, name in zip(pca.components_[0], pca.components_[1], df.columns[1:]):
ax1.text(x, y, name)
# 赤線のプロット
for i in range(11):
ax1.plot([-0.05, pca.components_[0][i]], [0.2,pca.components_[1][i]], c='r' )
# 主成分得点のプロット
for x, y, name in zip(feature[:, 0], feature[:, 1], df.iloc[:, 0]):
ax2.text(x, y, name,alpha=0.8)
ax2.scatter(feature[:, 0], feature[:, 1], alpha=0.8, c=list(df.iloc[:, 0]))
# グラフを編集する
ax1.set_ylim(-0.3,0.7)
ax1.set_xlim(-0.5,0.4)
ax2.set_ylim(-2,5)
ax2.set_xlim(-4,4)
handler1, label1 = ax1.get_legend_handles_labels()
handler2, label2 = ax2.get_legend_handles_labels()
ax1.legend(handler1+handler2,label1+label2,borderaxespad=0)
ax1.grid(True)
fig.show()
最後に
今回は、教師なし学習の一つである主成分分析を使用して、周期表を分析してみました!
主成分分析は、様々な分野のデータでも分析されています。
代表例で言うとマーケティングなどがあります。
もし興味がある方はぜひ分析してみてください!
22日目は@kswさんの「Gopacketでパケットをキャプチャしたり生成したりしてみる」です。
お楽しみに!!