【論文】メタ強化学習による因果推論

著者

• Deepmind, UCL, Harvardの研究者によるICLR2019への投稿論文(underreview)

概要

因果推論をメタ強化学習によるアプローチで解いていく、という新しい手法の提案。

• モデルフリーによる学習を通じたメタ強化学習により、因果の関係性に対する回答を解くタスクを解く
• 因果関係を正しく推定出来ていると高速に学習できる、という性質を利用して、因果関係の推定をする
• 既存のアルゴリズムのようなヒューリスティックではない因果推論の枠組みの提案

強化学習を用いた理由

• データを観察するだけではなく、介入によって変化を加えた後の因果と影響を考慮したい
  • 強化学習の枠組みで言うと、エージェントに介入操作のアクションを取らせて、他のノードへの影響を考慮する

メタ学習を用いた理由

• EndtoEnd+少ない計算で、スケーラビリティがあり、最も適した因果構造の内部表現を見つけるポテンシャルがあるアルゴリズムだから

事前知識

因果推論(causaul reasoning)とは

• 「このマーケティングの施策は売上を引き起こしたか」、「喫煙がガンを引き起こしましたか」のような、原因と結果について推論すること
• この論文ではグラフィカルモデルベースの因果推論アプローチを取っている
  • ちなみにcausaul inferenceはcausaul reasoningの一種
    • ざっくり言うと、inferenceは推定をして因果関係を定量的に出すが、reasoningは因果構造を把握するようなニュアンス

メタ学習とは

• メタ学習

  • 与えられた複数のタスクやドメインを使って、学習対象となるタスクやドメインに対する学習器のバイアスを決定するためのメタ知識を獲得する

• メタ強化学習

  • 与えられた複数のMDPを使って、学習対象となるMDPに対するエージェントのバイアスを決定するためのメタ知識を獲得する

• ざっくり言うと、汎用性があるような学習方法(メタ的要素)を学習する

  • トレーニング中に遭遇したことがないような新しいタスクには普通の機械学習だと適用できない
  • 例えば、強化学習でシミュレーションで学習して、現実のロボットに試したりする状況があるけど、実際はシミュレーション(学習中の環境)と現実の環境(テスト時の環境)は違う

Causal Bayesian networks (CBN)とは

• 因果関係を表す、DAG(directed acyclic graph)のグラフィカルモデル

• それぞれのノード$X_{i}$は確率変数に対応している

  • それらの同時分布$p(X_{1},...,X_{n})$は$\Pi_{i=1}^{N}p(X_{i}|pa(X_{i}))$(伝承サンプリング)で表される
    • $pa(X_{i})$は$X_{i}$の親ノード

• $X_{i}$から$X_{j}$に有向パスがあるとき、$X_{i}$は$X_{j}$の潜在的因果である

  • $X_{j}$は$p(X_{j}|X_{i})$で表せる

• A(年齢)、H(心臓の健康度合い)、E(1週間の運動時間)だとすると、

  • Aは交絡因子と呼ばれていて、因果の影響と非因果的影響がわからない
  • 例えば、EとHの相関関係は、A(交絡因子)による影響があるため、単純にEの変化によりHが変化するかどうかは分からない

• Aは交絡因子と呼ばれて、EとHに影響を及ぼす

因果関係の推論

• 因果推論の手法であるdo-calculusメソッドにより、図の(a)は(b)に置き換える事ができる

  • $E=e​$の因果効果は、$p(E|A)​$をデルタ関数$\delta​$で置き換えた、グラフ(b)の条件付き分布$p_{→E=e}(H|E=e)​$として見ることができる

    • pの分布が変わる事を強調したいので、上の表記で書いているが、これはいわゆる$ p(H|do(E =e))​$と同じ

  • do-calculusメソッドによって、グラフ(a)の観察からグラフ(b)の$p_{→E=e}(H|E = e)​$の計算が可能

    • この場合だと、$p_{→E=e}(H|E = e)=\sum_{A}p(H|E=e, A)p(A)^{2}$

    • 要はdo-calculusメソッドを使うと、グラフ(a)からの観察データであっても、グラフ(b)の中での推論が可能

      • do-calculusメソッドは詳しくは[こちら]が分かりやすい(https://www.inference.vc/untitled/)

• グラフ(a)のように交絡因子が観察される場合、上記のような推論が可能

  • ただし、観察されない交絡因子が存在する場合、グラフ(b)のような介入されたグラフから直接データを収集することで計算ができる
    • 例えば、グラフ(b)から$E=e$の値は固定しておき、残りの変数を観察する、ということ
    • これを本論文では、環境への実際の介入と呼んでいる
      • 次に出てくる介入的設定でのエージェントは、このような介入ができる

反事実的な推論

• 上記の因果関係の推論は、因果構造と交絡因子を考慮することによって、「運動は心臓の健康度を改善するか？」のような、予測問題に正しく答えることができる
  • ただし、反事実的な質問には答えることができない
    • 「心臓発作で無くなった個人に対して、もっと多くの運動をしたら、心臓の健康度はどうなるでしょうか」
    • つまり、(実際には起きなかった)反事実の世界での推論が必要
• このような反事実的な推論を行うためには、
  • 実際の世界からの観察+CBNを知ることで、個人に対する潜在的なランダム性を推定する
    • 例えば、その個人が心臓発作を起こした事から推測されるような変数(親の血圧とかその他の変数など。)
  • この推測値を利用して、運動をしたときの心臓の健康状態を計算することが出来る

定式化とアプローチ

3種類の実験

• 実験1:観測
  • エージェントは、環境からの観測のみ学習する
  • このデータによって、エージェントは相関関係を推論可能になり(連想推論)、環境の構造に応じて、因果的効果を可能にする(因果関係推論)
• 実験2:介入
  • いくつかの変数を設定し、他の変数への影響を観察することによって、環境内で行動することができる
  • このデータにより、因果効果の推定を容易にする
• 実験3:反事実
  • エージェントは最初に介入を通して、環境の因果構造を学ぶチャンスがある
  • エピソードの最後のステップでは、「前のタイムステップで、別の介入があったときにどうなっていたか」という反事実の質問に答える

グラフィカルモデルを利用して、この3つの設定でそれぞれで推論可能なパターンを形式化する。

タスク、設定、エージェントのアーキテクチャ

タスク

• エージェントはエピソード毎に違うCBN($\cal G​$)とやり取りをする
  • エピソードは２つのフェーズから成るTステップ
    • フェーズ1: 情報フェーズ
      • 最初のT-1ステップ回(つまり、最終ステップ以外)は、$\cal G​$から観察する、もしくは、介入した結果を観察する
      • このフェーズによって、$\cal G$の重みや結合が予測できる
    • フェーズ2: クイズフェーズ
      • フェーズ1で収集した情報から因果の知識から、ランダムな外部の介入の元での高い値を持つノードを選ぶ
      • 環境によって、観察できるノードの中からランダムに$X_{i}​$を選んで、介入をする(-5にセットする)

設定

• ノードの数(N)は$5$で、上三角の隣接行列を全通り作成する(DAGの条件を満たすため)
  • エッジの重みは${-1, 0, 1}$のいずれか。
  • $3^{N(N-1)/2}​$なので、全部で59049個のグラフになる
• 構造が同じだけど、ノードのラベルの順列が異なるようなグラフの集合
• テストセット
  • 12個の構造を持ったグラフ
    • " Our held-out test set consisted of 12 random graphs plus all other graphs in the equivalence classes of these 12. "が分からない…..
  • テストのグラフは、学習のときには見たことがない構造のもの
  • 全部で408個のグラフ
• それぞれのノード$X_{i}​$は正規分布に従う確率変数
  • 親なしノード: ${\cal N}(\mu=0, \sigma=0.1)$
  • 親がいるノード: $ p(X_{i}|pa(X_{i}))={\cal N}(\mu=\sum_{j}w_{ji}X_{j},\sigma=0.1)$ $(X_{j}\in pa(X_{i}))$
• 観察できない交絡因子の存在を考慮するため、$\cal G$のルートノードは観察できないようにしている
  • つまり、エージェントは他の4つのノードの値のみを観察できる
  • 4つのノードの値を全部結合した値:$v_{t}$

MDPの設定

($a_{t}$,$o_{t}$,$r_{t}$)

ここでは、$T=N=5$(つまり、情報フェーズT-1(4)、クイズフェーズ(1))

• アクション$a_{t}​$
  • 観察出来るノードはN-1個のため、2(N-1)個のアクション数がある
    • 情報フェーズのN-1個
    • クイズフェーズのN-1個
  • 違うフェーズのアクションを使用した場合、-10のペナルティ報酬を与えている
    • （メモ：フェーズごとに選択肢をマスキングして学習すれば良いのでは?一般的なやり方ではないのかな?）
  • 情報フェーズ
    • $a_{t}=i​$のとき、i番目のノードに介入して、$X_{i}=5​$にセットする
• 観察$o_{t}​$
  • $ o_{t} =[v_{t},m_{t}]$
    • $v_{t}$：観察した4つのノードの値を結合した値
      • 情報フェーズ
        • 介入されたCBNで$p_{→X_{i}=5}(X_{1:N{\backslash}i}|X_{i} = 5) $からサンプリングして$v_{t}$を得る
    • $m_{t}$：one-hot vector
      • 情報フェーズ
        • 基本的に0ベクトルだが、ステップ数が$T-1$のとき、クイズフェーズのときの介入をどのノードが得るか、のone-hot vectorになる
• 報酬$r_{t}$
  • 情報フェーズ
    • クイズフェーズのアクションを選ぶと$-10​$
  • クイズフェーズ
    • 選択されたノードの値が報酬となる
    • ただし、情報フェーズのアクションを選ぶと$-10$

エージェント

• LSTM
  • $[o_{t},a_{t−1},r_{t−1}] $を入力
  • 出力に線形変換、ソフトマックスしてアクション$a_{t}$をサンプリング
• 学習
  • A3C
  • ロス
    • policy gradient, baseline cost, entropy costの3つから成る
      • policy gradientの重みは1
      • baseline costの重みは0.05
      • entropy costの重みは0.25から0にアニーリングしていく
• Optimizer
  • RMSProp with ε=10−5
  • momentum = 0.9 and decay = 0.95
  • 学習率も$9×10^{−6}$から0にアニーリング
    • 割引率は0.93
• バッチサイズ:$1024​$
• 学習steps:$10^7​$回

実験

観察的設定

観察的設定の中では、4種類のアプローチを比較

• 通常の学習(Observational)
  • 情報フェーズでのエージェントのアクションを全て無視する
    • 観察されたデータのみを用いる(介入しない)
• エピソードを増やした学習(Long Observational)
  • Observationalのエピソードを増やした物
• Active Conditional
  • 選択したノードが$X_{j}=5$になっている世界で観察する
    • 残りのノードは$p(X_{1:N{\backslash}j}|X_{j}=5)​$からサンプリングしたい
    • 後で出てくる介入とは違って、${\cal G}$ではなく${\cal G}{→X{j}=5}$からサンプリングしたい
  • エージェントによるアクション
• Random Conditoinal
  • 上記と同じだが、ランダムによるアクション
• 最適解(Optiomal Associative Baseline)
  • 真の同時分布$p(X_{i:N})$を使用する(環境の構造を完全に把握している)
    • 言い換えると、$p(X_{j}|X_{i}=x)$は分かるが、$p_{→X_{i}=x}(X_{j}|X_{i}=x)$は分からない
    • クイズフェーズでは、真の分布$p(X_{j}|X_{i}=x)$に従ってサンプリングした最大値を持つノードを選択する
    • $X_{i}$は介入されたノードで、$x=-5$

結果

• Active-Condは最適解より良くなっている(a)
  • 親なしノードと親ありノードを比較すると、親ありノードのときに良くなっている(b)
  • つまり、do-calculusの本来の計算っぽい
• Active-CondがOptimial-Assocよりうまくいっている例(c)
  • 緑線は+1、赤線は-1、黒ノードは介入されたノード、青丸はクイズフェーズでエージェントの選んだ行動
• さらにActiveはRandomより良くなっている
  • 観察するためのデータ選択をエージェントが行っている

• 観察するだけだと、介入するより得られる情報が少ない

介入的設定

• アクティブ介入(Active Interventional)
  • 選択したノード$X_{j}​$の値を5にセット(介入)
    • 元のグラフ$\cal G​$ではなく、${\cal G}{→X{j}}​$からサンプリング
  • エージェントがアクションを選択
• ランダム介入(Random Interventional)
  • 上記と同じ
  • ランダムにアクションを選択

結果

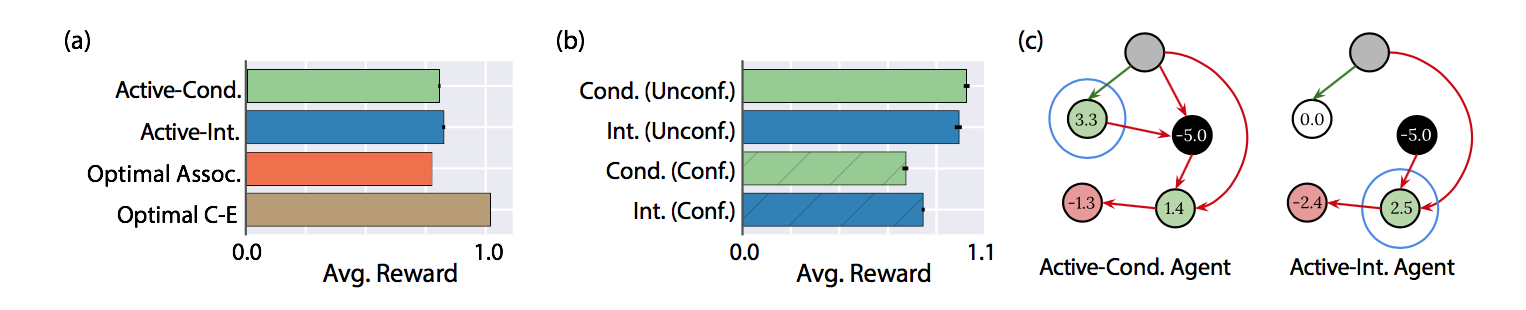
• Active ConditonalよりActive Interventionalの方が良い(a)
• 観察できない交絡因子がクイズフェーズ時に介入されたかどうかの比較(b)
• Active-Conditionalでは推論出来ず、Active Interventionalでは解決できるCBNの例(c)

反事実的設定

• 反事実的な設定を作成するために、$X_{i}=\sum_{j}w_{ji}X_{j}+\epsilon_{i} (\epsilon = {\cal N}(0, 0.1))$

• 1サンプル内のCBNのノードを観察した後、$X_{i}$について、$\epsilon_{i}$を推測する

• つまり、「観測した値と異なっていたときに、$X_{i}$はどうなるでしょう」という質問に答える

• 反事実的エージェント(Counterfactual Agents)

  • Interventional Agentとほぼ同じだが、情報フェーズの最終ステップで潜在的なランダムを加える
  • また、Interventional Agentは「$X_{f}$を-5にセットしたときに、残りの$X_{2:N}$が最も高い値を得るような、$X_{f}$はどれでしょう」という問だった
    • ここでは、「介入(+5)の代わりに、介入(-5)をしたとき、残りの$X_{2:N}$が最も高い値を持っているのか」という問題を解いている
      • （これで反事実的になっているのか、はよくわからなかった）

• ベースライン

  • 真のCBNを使用できる+観察に基づいて$\epsilon$が決まっている

結果

• 反事実的な設定を学習できていそう

• ランダムよりも良くなっているので、反事実的な設定でもエージェントを用いたほうがより因果の推定が出来ている事が分かる

サマリ

全体のサマリ

• メタ学習+モデルフリーの強化学習によるRNNの学習
• 3つの設定(観察的設定、介入的設定、反事実的設定)で因果推論
• 明示的な因果推論の式は使用しない
  • 因果構造に依存するタスクを実行するように最適化して、暗黙的に因果推論の戦略を学習
• これまでに見たことがない因果関係を持つグラフ構造でも、因果を推論できていた

観察的設定のサマリ

• 観測データだけを見て、因果関係の知識なしに達成可能な報酬よりも多くの報酬が得られた(図2a)

• 相関に基づいた予測と区別できるような、do-calculusに基づく予測は選択的に良い結果が得られた(図2b)

介入的設定のサマリ

• 観察データのみでは不可能である状況で、エージェントが介入をして、観察されていない交絡因子を推論できていた(図3)

反事実的設定のサマリ

• エージェントが反事実を学習した(図6)
• 特定のケースでは、パフォーマンスが向上している

感想・メモ

• ヒューリスティックな手法がある問題設定に対して、暗黙的に学習をするような強化学習のアプローチと、学習・テスト時に設定が変化するようなメタ学習を組み合わせて、因果推論という応用先は結構面白そうだった
  • 例えば、ルービックキューブを強化学習で解く手法などは、学習・テスト時で設定が変化しないが、今回の因果推論のCBNのように学習・テストで設定が変化するため、可能性を広げる意味で良さそう
• ただし、かなりきれいな世界での話
  • ノードは少ないし、ノイズを含めた、全てのノードは正規分布になっている
  • それと実際の応用例はまだ難しそう
• DAGベースの因果推論の知識がないと読みづらい...
• フェーズごとのRLのアクション選択に関してはマスクすれば良いかと思うけど、一般的なやり方ではない？
  • ルールを覚えるコストが発生するので、微妙そう