Go to Qiita Advent Calendar 2024 Top
LoginSignup
63
40

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

UnityAdvent Calendar 2017Day 19
@kodai100(Kodai Takao)

[#Unity] ComputeShaderで近傍探索の高速化

Last updated at Posted at 2017-12-18

unity.jpg

この記事は、Unity Advent Calender 2017 19日目の記事です。

はじめに

本記事では、かなり前に実装した
ComputeShaderで格子探索を行うアルゴリズムを解説します。

追記 : 卒論執筆で時間が取れずリポジトリの雑な説明になりそうです...すいません...

近傍探索

近傍探索とは、前もってデータ構造を最適化しておき、
値の利用時に全数探索をしないことで計算速度を飛躍的に向上させるアルゴリズムのことを指します。

主に使用される場面として、

があります。
いずれも物理的な2点間の距離を算出する必要があるアルゴリズムですが、
全数探索を行っていると、すべての要素毎にすべての要素との距離を計算する必要があります。
(俗に$O(n^2)$の実行時間を要すると言います)

当然この方法では、最新の筋肉GPUを用いても、8万程度の要素数でFPSの頭打ちが来てしまいます。
しかし、近傍探索を導入することで、64万程度の要素数でも余裕で60FPSをキープすることができるようになります。

現在、近傍探索にはいろいろな手法が存在し、代表例として

  • 四分木
  • 八分木
  • Kd木
  • 格子探索(この名称が存在するかは不明)

等があります。

GPUで実装する際には、単純に空間を格子状に分割する格子探索が最適とされています。
(～木系は再帰的に探索するためGPU上での実装が困難です。)

本記事では、この格子探索についての解説を行います。

格子探索のアルゴリズムと実装

本節の解説は以下のページに基づいています。
SPH法の実装(GPU実装含む)
こちらに掲載されている解説をComputeShaderに置き換えます。

解説に使用するリポジトリはこちらです。(※)
Unity_SpatialHashCS

データ構造の下準備

以下の図のような配置でパーティクルが空間に存在しているとします。

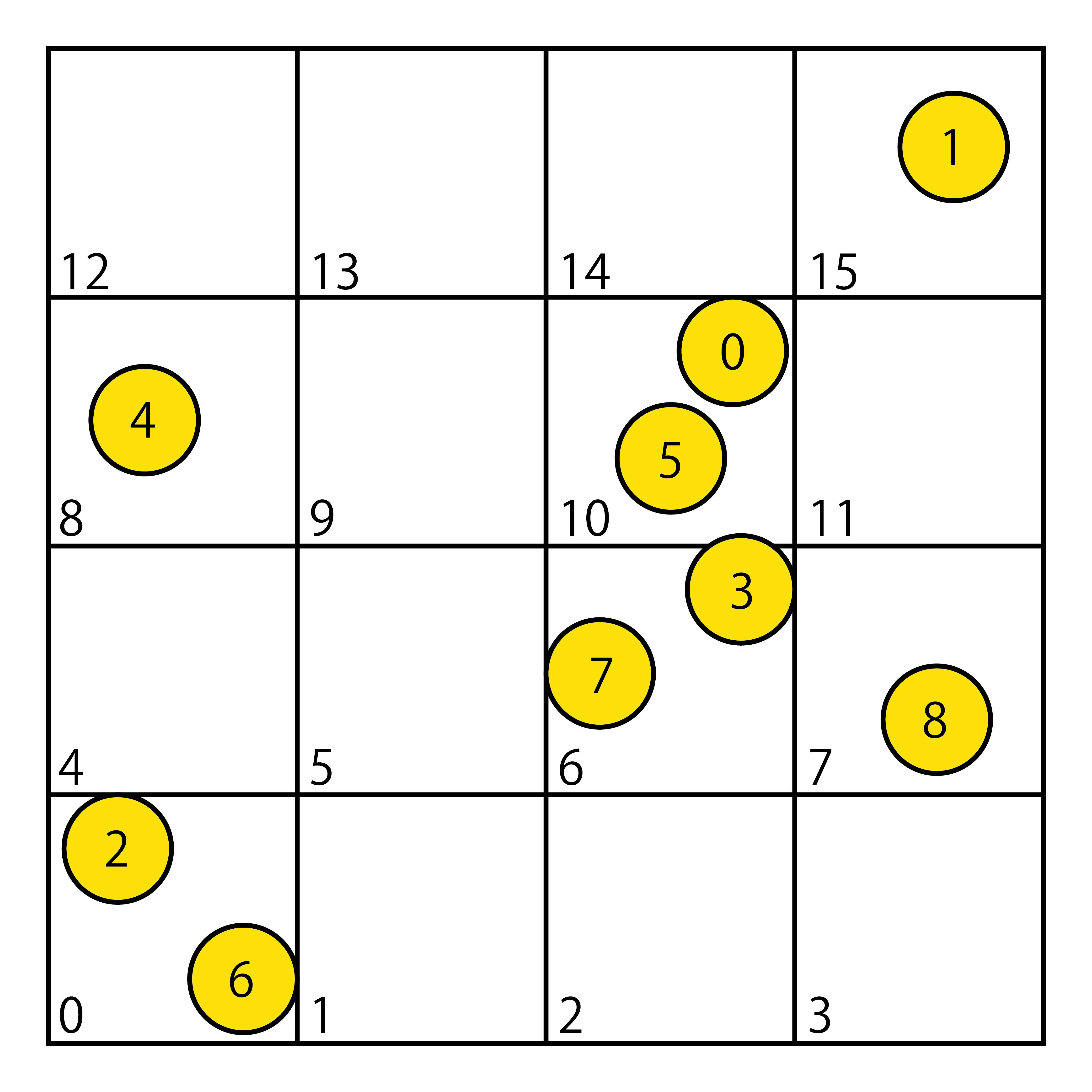
はじめに、以下の構造体で構成されたComputeBufferを、全パーティクル数分の長さで確保します。

data
struct uint2 {
    uint x;    // 格子のインデックス
    uint y;    // パーティクルのインデックス
}

2017-12-17_070555.jpg

次に、それぞれのパーティクルが属するセルを計算し、パーティクルインデックスとペアで保存します。

Grid2D.compute
[numthreads(SIMULATION_BLOCK_SIZE, 1, 1)]
void BuildGridCS(uint3 DTid : SV_DispatchThreadID) {
	uint P_ID = DTid.x;
	if (P_ID > (uint)(_NumParticles - 1)) return;

	float2 position = _ParticlesBufferRead[P_ID].pos;
	float2 grid_xy = GridCalculateCell(position);

	_GridBufferWrite[P_ID] = MakeKeyValuePair((uint2)grid_xy, P_ID);
}

2017-12-17_055722.jpg

次に、これを格子のインデックスで並び替えます。
ここで、パーティクルのインデックスも一緒に並び替えられることに気を付けておきましょう。
2017-12-17_055731.jpg
これを**表(3)**としておきます。

次に、以下の構造体で構成されたComputeBufferを、全格子数の長さで確保します。

data
struct uint2 {
    uint x;    // はじめ
    uint y;    // おわり
}

このとき、全要素を0xfff(値型の最大値)で初期化しておきます。

Grid2D.compute
[numthreads(SIMULATION_BLOCK_SIZE, 1, 1)]
void ClearGridIndicesCS(uint3 DTid : SV_DispatchThreadID) {
	_GridIndicesBufferWrite[DTid.x] = uint2(0xffffff, 0xffffff);
}

2017-12-17_051307.jpg

確保したバッファに対し、表(2)の格子インデックスが異なるものになる初めと終わりの番目を計算した結果を格納します。

Grid2D.compute
[numthreads(SIMULATION_BLOCK_SIZE, 1, 1)]
void BuildGridIndicesCS(uint3 DTid : SV_DispatchThreadID) {
	const unsigned int P_ID = DTid.x;
	uint P_ID_PREV = (P_ID == 0) ? (uint)_NumParticles : P_ID;
	P_ID_PREV--;
	
	uint P_ID_NEXT = P_ID + 1;
	if (P_ID_NEXT == (uint)_NumParticles) { P_ID_NEXT = 0; }

	uint cell = GridGetKey(_GridBufferRead[P_ID]);
	uint cell_prev = GridGetKey(_GridBufferRead[P_ID_PREV]);
	uint cell_next = GridGetKey(_GridBufferRead[P_ID_NEXT]);

	if (cell != cell_prev) {
		_GridIndicesBufferWrite[cell].x = P_ID;
	}

	if (cell != cell_next) {
		_GridIndicesBufferWrite[cell].y = P_ID + 1;
	}
}

2017-12-17_051322.jpg
これを**表(5)**とします。

ここまでで下準備は完了です。

近傍探索

表(3)と表(5)を利用して、近傍探索を行います。

今回の実装では、_DispIdxのIDを持ったパーティクルが属しているセルに属しているパーティクルすべてを赤色、
周辺のセルに属しているパーティクルすべてを水色にする処理を施しています。

ParticleProcess.compute
// 全パーティクルについて
[numthreads(SIMULATION_BLOCK_SIZE, 1, 1)]
void Update(uint3 DTid : SV_DispatchThreadID) {

	uint id = DTid.x;

	_ParticlesBufferWrite[id].color = float3(0, 0, 0);

	uint d = (uint)(_DispIdx > _NumParticles ? 0 : _DispIdx);
	if (id == d) {
		// Neighbor Search Area
		int2 G_XY = (int2)GridCalculateCell(_ParticlesBufferRead[id].pos);	// Calculate Own Cell Position (2D)

		// Loop Around Own Cell
		for (int Y = max(G_XY.y - 1, 0); Y <= min(G_XY.y + 1, _GridDim.y - 1); Y++) {
			for (int X = max(G_XY.x - 1, 0); X <= min(G_XY.x + 1, _GridDim.x - 1); X++) {
				unsigned int G_CELL = GridKey(uint2(X, Y));	// Calculate Neighbor (or own) Cell ID
				if (G_CELL == GridKey(G_XY)) {
					// if own cell, fill red
					uint2 G_START_END = _GridIndicesBufferRead[G_CELL];
					for (unsigned int N_ID = G_START_END.x; N_ID < G_START_END.y; N_ID++) {
						_ParticlesBufferWrite[N_ID].color = float3(1, 0, 0);
					}
				}
				else {
					// if neighbor cell, fill blue
					uint2 G_START_END = _GridIndicesBufferRead[G_CELL];
					for (unsigned int N_ID = G_START_END.x; N_ID < G_START_END.y; N_ID++) {
						_ParticlesBufferWrite[N_ID].color = float3(0, 1, 1);
					}
				}

			}
		}
	}

	_ParticlesBufferWrite[id].pos = _ParticlesBufferRead[id].pos;
}

バイトニックソート

今回のソーティングの実装では、@oishihiroaki先生のリポジトリからバイトニックソートを拝借しました。
UnityGPUBitonicSort - @oishihiroaki

※ 注意点として、ソート対象が2のべき乗の長さでなければならない制約があります。
つまり、今回の例ではパーティクル数が2のべき乗である必要があります。

バイトニックソートの解説については、またの機会にできればと思っております。

終わりに

雑な解説となってしまいましたが、最後までお付き合いいただきありがとうございました。
時間ができましたら、より詳しい解説を追記しようと思っております。

※ お詫び

何を血迷ったのか、まとまりのない実装になっている為ご容赦願います。
(2次元と3次元でジェネリック対応したかったのですが、加減乗除の対応が面倒で途中で諦めてしまいました...)

Unity Graphics Programming

Unityを用いたグラフィクスプログラミングの技術書を同僚と出版しました。 ご興味があればぜひご一読ください。 ストアリンク : [https://indievisuallab.stores.jp/items/59edf11ac8f22c0152002588](https://indievisuallab.stores.jp/items/59edf11ac8f22c0152002588)

目次
第1章 Unityではじめるプロシージャルモデリング
第2章 ComputeShader入門
第3章 群のシミュレーションのGPU実装
第4章 格子法による流体シミュレーション
第5章 SPH 法による流体シミュレーション
第6章 ジオメトリシェーダーで草を生やす
第7章 雰囲気で始めるマーチングキューブス法入門
第8章 MCMCで行う3次元空間サンプリング
第9章 Multi Plane Perspective Projection
第10章 ProjectionSprayの紹介

63
40
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
63
40

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?