OSMとturf.jsで、館林の最寄りバス停発見データを作ってみる (最寄りポリゴン生成編)

この記事はOpenStreetMap Advent Calendar 2020とTurf.js Advent Calendar 2020の21日目の記事(後半)になります。

何をやったかを簡単に

公共交通機関のあまり発展していない地方都市で、だからこそ少ない本数のバスを効率的に利用するために、最寄りのバス停を発見するためのデータを作ってみました。
前半後半に分かれており、この記事では後半の、Turf.jsを使って最寄りポリゴンを生成するところを書きます。
先に前半の記事を読んでください。

最寄りバス停を計算

前半では、バス停や鉄道駅、バスルート、市町村境など、処理の基礎になるデータをOSMから抽出してみました。
後半では、これらの基礎データを元に、最寄りバス停(及び鉄道駅)を求めるデータを作成してみましょう。
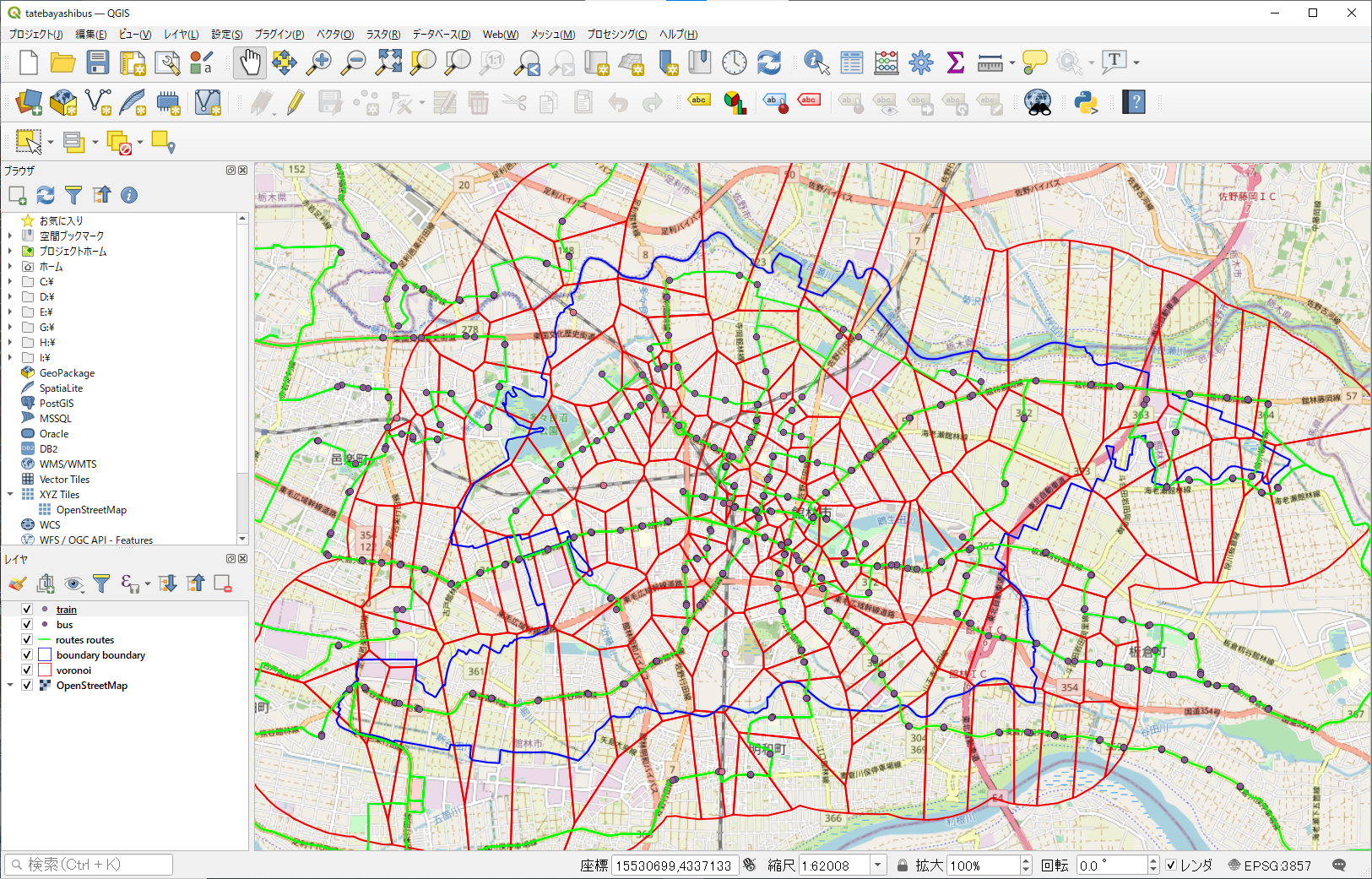
最寄りバス停というのは、他のバス停よりもこのバス停の方が近い地点をまとめたポリゴンを生成すれば求められ、これは点群の「ボロノイ図」というものを計算をすれば求められます。
もちろん、厳密には距離でなく道のりで計算されるべきですし、川や湖など踏破できない場所は考慮して計算されるべきなのですが、飽くまで目安としてなら、十分ボロノイ図で対応可能でしょう。
ボロノイ図の計算には、turf.jsの@turf/voronoiが利用できます。

では、導出戦略を示してみます。

1. バス停データは、同じ名前のバス停が上りバス停と下りバス停で2つ地点が定義されています。
   これを別と考えて最寄りポリゴンを複数に分けるのもバカらしいので名寄せします。
   平均位置は、厳密には球面上の距離計算などで出すべきですが、ごく狭い領域なので経緯度の加重平均で問題ないでしょう。
2. 名寄せ後のバス停データは、あまり館林市から遠いところのバス停を計算しても仕方ないので、館林市の境界を元にフィルタします。
   ただし、境界で厳密に切ってしまうと、隣町の境界ギリギリのバス停の方が実は近かったというようなところが出てしまうので、境界でぶつ切りではなく、境界から外に2kmほど膨らんだところで切ります。
   境界ポリゴンを元に外にバッファを持ったポリゴンの生成は、@turf/bufferで求められ、ポリゴンの中に含まれるかのフィルタ判定は@turf/boolean-point-in-polygonで判定できます。
3. 同じく、鉄道駅もフィルタして、バス停名寄せデータにマージします。
4. マージした名寄せバス停・鉄道駅データから、@turf/voronoiでボロノイ図を生成します。
5. できたボロノイ図は、はるか地球の裏側まで含めたポリゴンになっています。
   先に@turf/voronoiの引数にバウンディングボックスを与えて範囲を制限することもできるのですが、せっかく市町境から2kmのバッファポリゴンを作っているので、それでボロノイ図をくりぬきましょう。
   ポリゴン同士を重ね合わせて重複部分をくりぬく処理は、@turf/intersectで求められます。

これをnode.jsコードに示してみるとこのような感じになります。

index.js

const fs = require('fs');
const voronoi = require('@turf/voronoi');
const buffer = require('@turf/buffer');
const booleanPointInPolygon = require('@turf/boolean-point-in-polygon').default;
const intersect = require('@turf/intersect').default;

const bus = JSON.parse(fs.readFileSync('./bus.geojson'));
const train = JSON.parse(fs.readFileSync('./train.geojson'));
const boundary = JSON.parse(fs.readFileSync('./boundary.geojson'));
// 市町境から2kmのバッファポリゴン生成
const bufferBoundary = buffer(boundary.features[0], 2);

// バス停データを名寄せ処理
bus.features = bus.features.reduce((prev, curr, index, arr) => {
  const name = curr.properties.name;
  if (!prev[name]) prev[name] = [];
  prev[name].push(curr);
  if (index !== arr.length - 1) return prev;
  return Object.keys(prev).map((key) => {
    return prev[key].reduce((prev, curr, index, arr) => {
      if (!prev) {
      	prev = curr;
      	prev.num = 1;
      } else {
      	prev.geometry.coordinates[0] += curr.geometry.coordinates[0];
      	prev.geometry.coordinates[1] += curr.geometry.coordinates[1];
      	prev.num++;
      }
      if (index !== arr.length - 1) return prev;
      prev.geometry.coordinates[0] /= prev.num;
      prev.geometry.coordinates[1] /= prev.num;
      delete prev.num;
      return prev;
    }, null);
  });
}, {}).filter((item) => { // バッファポリゴンでフィルタ
  return booleanPointInPolygon(item, bufferBoundary);
});

// 鉄道駅データをフィルタしたうえで、名寄せ済みバス停データにマージ
train.features.filter((item) => {
  return booleanPointInPolygon(item, bufferBoundary);
}).map((item) => {
  bus.features.push(item);
});

// ボロノイ図生成
const voronoiObj = voronoi(bus);
// ボロノイ図をバッファポリゴンでくり抜き
voronoiObj.features = voronoiObj.features.map((item) => {
  return intersect(item, bufferBoundary);
}).filter((item) => {
  return item ? true : false;
});

// くり抜かれたボロノイ図を voronoi.geojsonの名前でセーブ
fs.writeFileSync('./voronoi.geojson', JSON.stringify(voronoiObj));

以上までで生成した

• bus.geojson
• train.geojson
• routes.geojson
• boundary.geojson
• voronoi.geojson

をまとめてQGISで表示すると、こんな感じになります。

==========================================
以上、OSMデータ、Overpass Turboとturf.jsを使って、無事館林市内の最寄りバス停を判定できるデータができました。
実際の街歩きに使うには、各バス停と時刻表のデータを紐づけるなどいくつかさらに手順が要りそうですが、とりあえず今回はここまでです。