※この記事はUEQareer Advent Calender 2016 17日目の記事です。
はじめに
私は普段MATLABを利用して信号処理の研究をしています.今回は圧縮センシングと呼ばれる信号処理技術をMATLABを利用して紹介したいと思います.
圧縮センシング
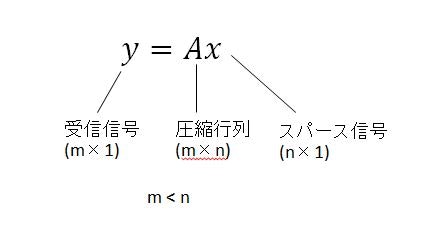
圧縮行列が既知の時,受信信号からスパース信号を復元するのが圧縮センシングです.一般的にm<nのときこの問題を解くことは困難ですが,”スパース(多くの要素が0)”という条件がある場合に圧縮センシングが利用可能になります.
無線通信の分野では圧縮センシングの技術を無線信号をサンプリングする装置に適用することで,従来よりも少ないサンプリング周波数で信号を取得し,サンプリング装置での消費電力の削減や,より広い電波空間の取得,無線信号データのトラフィックの軽減などが期待されています.
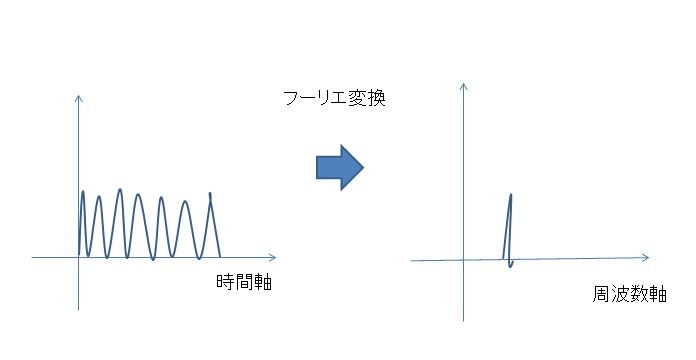
無線通信の分野では,信号をフーリエ変換し周波数帯で見ることでスパースな性質が得られるため圧縮センシングが利用されます.
受信信号の生成
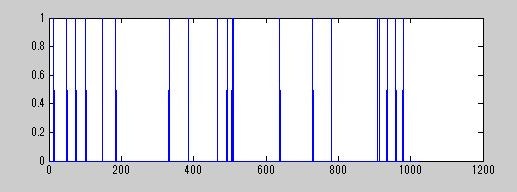
1024次元の20-スパース信号(非ゼロ要素が20個)を圧縮行列により128次元に圧縮して受信信号を生成してみます.
k = 20; %kスパース
n = 1024;%圧縮前の次元数
m = 128;%圧縮後の次元数
%スパース信号の生成(今回はシンプルにランダムに20個の大きさ1を持つスパース信号を生成)
x = zeros(n,1);
index = randperm(n,k);
for i = 1:k
x(index(i)) = 1;
end
%圧縮行列 A(ランダム行列とフーリエ逆変換行列からなる)
%Θ(ランダム行列)M*N
%圧縮センシングの圧縮にはランダム行列が用いられ、ランダム行列の研究もおこなわれている.今回はシンプルにガウスランダム行列を使用します.
O = rand(m,n);
%φ(基底行列)n*n 実際に受信する信号は時間系列データなので逆フーリエ変化で時間系列データに変換します.
F = dftmtx(n);
reF = conj(dftmtx(n))/n;
A = O * reF;
%受信信号 y
y = A * x;
plot(x);% 元のスパース信号の表示
復元アルゴリズム
圧縮センシングにおける復元(受信信号からスパース信号を推定する)アルゴリズムには貪欲法であるorthogonal matching pursuit(OMP)や基底追跡法である Basis pursuit (BP)がある.OMPはBPと比較して計算量が少ないですが復元制度が落ちます.今回はOMPを実装したmatlabのコードを紹介します.
アルゴリズムの詳細は”圧縮センシング-疎情報の再構成とそのアルゴリズムー”を見ていただくと日本語でわかりやすいかと思います.
function [x res ] = omp(y,A,k)
[m,N] = size(A);
x = zeros(N,1); %復元するスパース信号の初期値はすべて0
res = y; %初期値は受信信号
column = [];
for i=1:k
[c n] = max(abs(A'*res)); %内積をとり受信信号と関連の強い列を選択
column(end+1) = n; % end+1 で配列の後ろに要素を追加できる 先ほど選択した列番号を追加
x(column) = pinv(A(:,column))*y; %pinv():疑似逆行列 スパース行列の計算
res = y - A(:,column)*x(column);
end
end
上記のOMPアルゴリズムでは貪欲法により圧縮行列からk個の列を選択してスパース行列を復元します.そのため復元したスパース行列の非ゼロ要素数はk個になります.
上記の復元アルゴリズムを使用する際にはあらかじめ復元する信号のスパース度(非ゼロな要素数)を知っておく必要があります.
復元の実行結果
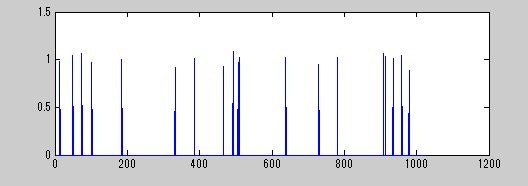
生成した20-スパースの受信信号を上記のOMPアルゴリズムを用いて復元させます.
[xp res]= omp(y,A,k); %xpに復元信号が返ってくる
plot(abs(xp));% 復元信号の表示
ほぼ正確に復元できていることが確認できました.
最後に
圧縮センシングのシンプルな例をMATLABのコードで非常にざっくりと紹介しました.圧縮センシングはmatlabのリファレンスが少なく実装に苦労しています.
圧縮センシングを実装するにあたり参考になるサイトや資料をご存知の方がいらっしゃいましたら教えて頂けると幸いです.