LoginSignup
0
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@kobae964

競プロの双対性: Segtree さんの問題編

Last updated at Posted at 2025-07-31

Segtree さんが競プロの双対の問題を出しているので解説する。

(1)-(10)

ということなので、この 10 問については準線型時間 (quasilinear time) で解く方法も書く。一点更新 query を対数時間で処理する方法も書く。

(1) 未解決

まだ解けていない

(2)

各頂点に整数重みA[i]が付いたN頂点の根付き木について、以下の存在命題と同値な全称命題は？

「iがjの先祖であるような(i,j)を選び、A[i]から1を引き、A[j]に1を足す」操作を繰り返して、Aの全ての要素を0にできる

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

wata さんのスライドの p.47 を参照する。元の命題は以下のように言い換えられる:

$N$ 頂点のネットワークがあり、頂点 $i$ の流入は $A[i]$ である。また元々の根付き木の親から子へ、容量 $\infty$ の辺がある。このネットワークでフローを流すのは実行可能である。

まず、流入の和が 0 である必要があるので、 $\sum_v A[v] = 0$ である。今回のように実行可能性を調べる場合は、辺のコスト $w_{uv}$ は 0 としてよい。また $p_v = 0 (\forall v)$ が常に実行可能解 (値が 0) を与え、 $p$ を $k \ge 0$ 倍すると値も $k$ 倍になるので、双対問題 $\min \sum_v b_v p_v+ \sum_{uv} c_{uv}\max(0, p _ v - p _ u)$ の解としてあり得るのは以下の 2 パターンのみである:

  1. 最小値は 0 である。つまり $\sum_v b_v p_v+ \sum_{uv} c_{uv}\max(0, p _ v - p _ u) \ge 0$ が任意の $p$ に対して成り立つ。
  2. 最小値は存在せずいくらでも小さい値をとることができる。 $-\infty$ と言ってもよい。

1. が元の命題と同値である。今回の場合、 $c_{uv} = \infty$ であるため、 $p _ v - p _ u$ がちょっとでも 0 を上回ると最小化問題の答えにはならなくなる。よって、 $(\forall uv \in E\ldotp p_u \ge p_v) \Rightarrow \sum_v A[v] p_v \ge 0$ と同値である。

ここで、天才考察 (TODO) を行うと、$p$ として考えるべきものはある部分根付き木の上で $p_i = -1$、そうでないところで $p_i = 0$ のものだけであることがわかるので、以下の命題と同値であることが結論できる。

$\sum_v A[v] = 0$ かつ 全ての部分根付き木に対し、 $\sum_v A[v] \le 0$

(3)

長さNの整数列Xについて、以下の存在命題と同値な全称命題は？

「任意のiについて、i番目の頂点の入次数-出次数がX[i]である」 ようなN頂点の単純有向グラフが存在する。

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

(2) と同じように考察する。同値なフローの問題は以下である:

$N$ 頂点のネットワークがあり、頂点 $i$ の流入は $X[i]$ である。また各ペア $i \ne j$ に対し、 $i$ から $j$ へ容量 $1$ の辺がある。このネットワークでフローを流すのは実行可能である。

流入の和は 0 なので $\sum_i X[i] = 0$ である。双対問題をとると以下のようになる。

任意の $p$ に対して $\sum_i X[i] p_i+ \sum_{ij} \max(0, p _ j - p _ i) \ge 0$

ここで、天才考察 (TODO) を行うと、 $p$ として考えるべきものはある頂点の部分集合 $S$ の上で $p_i = 1$、そうでないところで $p_i = 0$ のものだけであることがわかるので、以下の命題と同値であることが結論できる。

$\sum_i X[i] = 0$ かつ 任意の頂点の部分集合 $S$ に対して $\sum_{i \in S} X[i] + |S|(N - |S|) \ge 0$

(4)

長さN+Mの非負整数列Xについて、以下の存在命題と同値な全称命題は？

「任意のiについて、i番目の頂点の次数がX[i]である」 ような、頂点1,…,Nのいずれかと頂点N+1,…,N+Mのいずれかを結ぶ辺のみが存在する単純無向二部グラフが存在する。

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

(2) と同じように考察する。同値なフローの問題は以下である:

$N + M$ 頂点のネットワークがあり、頂点 $i$ の流入は $X[i]$ ($1\le i \le N$) あるいは $-X[i]$ ($N+1 \le i \le N+M$) である。また各ペア $1 \le i \le N, 1 \le j \le M$ に対し、 $i$ から $N + j$ へ容量 $1$ の辺がある。このネットワークでフローを流すのは実行可能である。

流入の和は 0 なので $\sum_i X[i] = \sum_j X[N+j]$ である。双対問題をとると以下のようになる。

任意の $p$ に対して $\sum_i X[i] p_i - \sum_j X[N+j] p_{N+j}+ \sum_{ij} \max(0, p _ {N+j} - p _ i) \ge 0$

(3) と同じ天才考察により以下が同値であることがわかる。

$\sum_i X[i] = \sum_j X[N+j]$ かつ 任意の頂点の部分集合の対 $(S \subseteq \lbrace 1,\ldots, N\rbrace, T \subseteq \lbrace N+1,\ldots, N+M\rbrace)$ に対し、 $\sum_{i\in S} X[i] - \sum_{j \in T} X[j] + |T|(N - |S|) \ge 0$

(5)

二次元平面上にN個の直線A[i]x+B[i]y=C[i]がある(C[i]!=0) 。以下の最大化問題と等しい最小化問題は？

原点を中心とした、どの直線とも交差しないような円の半径の最大値

類別: Lagrange 双対

解法

円の半径 $r$ は直線の原点からの距離以下 ($r \le |C[i]|/\sqrt{A[i]^2 + B[i]^2}$) であるため、 $|C[i]|/\sqrt{A[i]^2 + B[i]^2}$ の最小値が答えである。

以上の考察を Lagrange 双対として定式化することができる。一般性を失わず $C[i] > 0$ を仮定して良い。問題は $s^2+t^2 = 1, A[i]x + B[i]y \le C[i]$ の条件で $sx + ty$ を最大化し、 $(s, t)$ を動かして最小値を求める問題とみなせる。Lagrange 緩和すると、 $u_i \ge 0$ として
$\sup_{x,y} sx+ty - \sum_i u_i (A[i]x + B[i]y - C[i])$ を最小化する問題とみなせる。

$$g(x, y) := sx+ty - \sum_i u_i (A[i]x + B[i]y - C[i])$$

とおくと、

$$\partial g/\partial x = s - \sum_i u_i A[i]$$

$$\partial g/\partial y = t - \sum_i u_i B[i]$$

が成立する。これらのうちどちらかが非ゼロである場合、 $g(x,y)$ は一次式であり $(x, y)$ の範囲に制限はないため、 sup が際限なく大きくなってしまう。よってこれらが両方とも 0 である必要がある。

以上をまとめると、 $(\sum_i u_i A[i])^2 + (\sum_i u_i B[i])^2 = 1, u_i \ge 0$ の条件下で $g = \sum_i u_i C[i]$ を最小化する問題になる。これは $u_i$ のうち一つだけ非ゼロで残りがゼロの場合に最小値が達成される。 (TODO: $g$ を固定して二乗和を最大化する問題とみなすことで証明する)

$u_i$ が非ゼロだとすると $u_i = 1/\sqrt{A[i]^2+B[i]^2}$ であり、このとき $g = C[i]/\sqrt{A[i]^2+B[i]^2}$ である。

(6) 未解決

まだ解けていない

(7)

N頂点の根付き木と、組(u,v,d) の形の制約M個に対して、以下の最大化問題と等しい最小化問題は？

各制約について、u→vパスの重みがd以下となるように、各辺に非負の値w[i]を与える。
ただし、各辺の重みは根に向かう方向に辿るときw[i], そうでないとき-w[i]。
1→Nパスの重みの最大値

類別: 最小費用流 (MCF) の双対

解法

あらかじめ以下のように言い換えておく。答えを -1 倍して最小化問題に変換する。

$N$ 頂点の根付き木の各頂点にポテンシャル $p_v$ を定める。 $uv$ が親子のとき $p _ u \le p _ v$ であり、制約 $(u, v, d)$ に対して $p _ v \le p _ u + d$ である。このとき $p _ 1 - p _ N$ を最小化せよ。

これは $p _ 1 - p _ N + \sum_{uv: \text{親子}} \infty \max(0, p _ u - p _ v) + \sum_{(u, v, d): \text{制約}} \infty \max(0, p _ v - p _ u - d)$ という形に変換できる。wata さんのスライドの p.47 を参照する。言い換えた後の問題の双対は以下である:

$N$ 頂点のネットワークがあり、頂点 1 への流入は 1、頂点 N への流入は -1 である。

  • 元々の根付き木の子から親へ、容量 $\infty$ コスト $0$ の辺がある。
  • 制約 $(u, v, d)$ に対して、$u$ から $v$ へ容量 $\infty$ コスト $d$ の辺がある。

このネットワークにおける最小費用流を求めよ。

この問題は辺の容量が 1 でも答えが変わらず、そのため最短路問題と等価である。制約の個数を $M$ とすると計算量は $O((N+M) \log N)$ 時間などである。

(8)

長さNで総和が0の整数列Aについて、以下の最大化問題と等しい最小化問題は？

任意のiで|B[i]-B[(i+1)%N]|<=1であるような長さNの数列Bについて、ΣA[i]*B[i] の最大値

類別: 最小費用流 (MCF) の双対

解法

(2) と同様に考察する。最小化すべきものは $\sum_i -A[i]B[i] + \sum(\infty\max(0, B[i] - B[(i+1)\bmod N] - 1) + \infty\max(0, B[i] - B[(i+N-1)\bmod N] - 1))$ である。双対をとると以下のような最小費用流の問題になる。

円環状の $N$ 頂点のネットワークがあり、頂点 $i$ の流入は $-A[i]$ である。また容量 $\infty$ コスト $1$ の辺が双方向に隣同士の頂点を結んでいる。このネットワークにおける最小費用流を求めよ。

なおこの問題は双対に関係なく以下のように解ける。

$P[i] := B[i] - B[(i+N-1)\bmod N]$ とおき、$C[i] := A[i] + \cdots + A[N-1]$ とおくと、 $P[0] + \cdots + P[N-1] = 0$ かつ $\sum A[i]B[i] = \sum C[i]P[i]$ である。

$-1 \le P[i] \le 1$ の条件下で $\max \sum C[i]P[i]$ を求めれば良いので、 $C$ をソートして上位 $\lfloor N/2 \rfloor$ 個の和から下位 $\lfloor N/2 \rfloor$ 個の和を引けば良い。 $O(N \log N)$ 時間である。

類題:

(9) 未解決

まだ解けていない

(10)

2×Nグリッドにいくつかの赤いマスと青いマスが存在する。赤いマスは、x座標とy座標が共に自分以下の青いマスとマッチングできる。以下の存在命題と同値な全称命題は？

全ての赤いマスを相異なる青いマスにマッチングできる

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

(2) と同じように考察する。同値なフローの問題は以下である:

$2 \times N$ 頂点のグリッド状のネットワークがあり、赤い頂点の流入は $1$ で、青い頂点の流入は $-1$ である。また $(1, N-1)$ に、合計で流入が $0$ になるように追加の流入がある (これは $0$ 以上である)。また左と下へ向かう容量 $\infty$ の辺がある。このネットワークでフローを流すのは実行可能である。

頂点 $(i, j)$ が赤の場合 $X_{i,j} = 1$ 、青の場合 $X_{i,j} = -1$ 、それ以外の場合 $X_{i,j} = 0$ とする。
これらの和は 0 以下なので $R = \sum_{i,j} X_{i,j} \le 0$ である。双対問題をとると以下のようになる。

任意の $p$ に対して $\sum_{i,j} X_{i,j} p_{i,j} - R p_{1,N-1}+ \sum_{i,j} \infty \max(0, p _ {i,j} - p _ {i,j + 1}) + \sum_{j} \infty \max(0, p _ {0,j} - p _ {1,j}) \ge 0$

ここで、天才考察 (TODO) を行うと、 $p$ として考えるべきものはある $j_0 \ge j_1$ について $(0,0), \ldots, (0, j_0 - 1), (1, 0), \ldots, (1, j _ 1 - 1)$ の上で $p_i = 0$、そうでないところで $p_i = 1$ のものだけであることがわかるので、以下の命題と同値であることが結論できる。

任意の $j_0 \ge j_1$ に対して $\sum_{i, j < j_i} X_{i,j} \le 0$

これは累積和などを使えば $O(N)$ 時間で判定できる。

一点更新 query を $O(\log N)$ 時間で行う方法は以下である。 $(\mathrm{add}, \mathrm{max})$ 遅延セグメント木を 3 本用意し、 $S_0, S_{0\mathrm{max}}, S_{\mathrm{all}}$ と呼ぶ。

$S_0$ は $X_{0,?}$ の (左からの) 累積和、 $S_{0\mathrm{max}}$ は $S_0$ の右からの累積 max、$S_{\mathrm{all}}$ は $S_{0\mathrm{max}}$ と $X_{1,?}$ の累積和の和を管理することにする。可能かどうかは $S_{\mathrm{all}}$ の全体の max が 0 以下かどうかで判定する。$X_{?,?}$ に 1 を足したり引いたりする操作に対応できれば良い。

$X_{1,i}$ に足し引きするのは、 $S_{\mathrm{all}}$ の $[0, i]$ に足し引きすれば良い。
$X_{0,i}$ に足し引きするとき、以下のステップを行う。最終的にやりたいのは $S_0$ の $[0, i]$ に足し引きすることである。

  • $S_0$ の $[0, N]$ に足し引きする。連動して $S_{0\mathrm{max}}$ も $S_{\mathrm{all}}$ も変更するが、これも同じ値を全体に足し引きすれば良い。
  • $S_0$ の $[i + 1, N]$ に足し引きする。
    • 1 を足す場合、 $S_{0\mathrm{max}}$ が単調減少であることに注意すると、 $S_{0\mathrm{max}}[j] = S_{0\mathrm{max}}[i+1]$ であるような $j$ の範囲に 1 を足せば良い。 $S_{\mathrm{all}}$ の同じ範囲にも 1 を足す。
    • 1 を引く場合、まずは $S_{0\mathrm{max}}$ の $[i+1, N]$ から 1 を引く。 $S_{0\mathrm{max}}[i+1]$ の古い値を $x$ とする。 $S_{0\mathrm{max}}[j..i+1] = x$ となる範囲の一部から 1 が引かれるのでその範囲を求めることになる。その範囲は $S_{0\mathrm{max}}[k] = x$ となる最大の $k \le i$ を取った場合 $[k + 1, i]$ である。$S_{\mathrm{all}}$ の同じ範囲からも 1 を引く。

(11)-(20)

(11)

N頂点の無向グラフについて、以下の存在命題と等しい全称命題は？

奇数長の単純閉路が存在する。

類別: rank-nullty theorem 線型方程式

解法

任意の色割り当て $f \colon V\to \lbrace 0,1\rbrace$ に対して、 $f$ は 2-彩色ではない。つまり $f(u) = f(v)$ なる辺 $uv$ が存在する。

これを線形代数の概念で説明すると以下のようになる。有限体 $\mathbb{F}_{2}$ の上で議論を行う。

$M$ を辺の本数として、 $A$ を $N \times M$ の接続行列 とするとき、奇数長の単純閉路が存在することと以下は同値である:

(i): $\exists b \in \mathbb{F}_{2}^M \ldotp \begin{pmatrix}A \\ {}^t1_M\end{pmatrix} b = \begin{pmatrix}0_N \\ 1\end{pmatrix}$

また、2-彩色がないことと以下は同値である:

(ii): $\forall d \in \mathbb{F}_{2}^N \ldotp {}^td A \neq {}^t1_M$

(i) は $\mathop{\mathrm{rank}}\begin{pmatrix}A \\ {}^t1_M\end{pmatrix} = \mathop{\mathrm{rank}} \begin{pmatrix}A & 0_N \\ {}^t1_M & 1\end{pmatrix}$ と同値である (参考: https://chatgpt.com/share/68afe6e1-71e8-8010-9c67-43f878c98d8e) $A$ を行ベクトルの変換としてみなして次元を計算すれば $\mathrm{rank} \begin{pmatrix}A & 0_N \\ {}^t1_M & 1\end{pmatrix} = \mathop{\mathrm{rank}} A + 1$ は明らかである。よって $\mathop{\mathrm{rank}}\begin{pmatrix}A \\ {}^t1_M\end{pmatrix} = \mathop{\mathrm{rank}} A + 1$ と同値である。

(ii) は $A$ を行ベクトルの変換とみなしたときに ${}^t1_M$ が像に入っていないという主張なので、${}^t 1_M$ を追加したら rank が $1$ 増える、つまり $\mathop{\mathrm{rank}}\begin{pmatrix}A \\ {}^t 1_M\end{pmatrix} = \mathop{\mathrm{rank}} A + 1$ と同値である。

よって (i) と (ii) は同値である。

(12)

正整数Nについて、以下の最大化問題の答えは？

1~Nの整数の部分集合であって、約数/倍数関係にあるペアが存在しないようなもののサイズの最大値は？

類別: Dilworth の定理

解法

約数/倍数関係 (整除関係) は推移的な関係である ($a | b$ かつ $b | c$ なら $a | c$) 。よって Dilworth の定理から、

$$(\text{最大独立集合の大きさ}) = (\text{最小パス被覆の大きさ})$$

が成り立つ。そのため同じ大きさの独立集合とパス被覆を構築すれば良い。

  • 集合 $\lbrace \lfloor N/2\rfloor + 1, \ldots, N \rbrace$ は大きさ $\lceil N/2 \rceil$ であり、どの二要素も整除関係にない。
  • $1$ 以上 $N$ 以下の奇数 $c$ それぞれに対してパス $c \to 2c \to \cdots 2^kc$ ($k$ は $2^kc \le N$ を満たす最大の非負整数) を考えると、これらのパスはちょうど $\lceil N/2 \rceil$ 個あり $\lbrace 1, \ldots, N \rbrace$ を被覆する。

よって Dilworth の定理から答えは $\lceil N/2 \rceil$ である。

(13)

N個の文字列S1,…,Snについて、以下の最大化問題の答えは？

どの文字列どうしも「片方が片方のsuffix」という関係にないような添字集合のサイズの最大値

類別: Dilworth の定理

解法

suffix かどうかの関係は推移的な関係である。よって Dilworth の定理から、

$$(\text{最大独立集合の大きさ}) = (\text{最小パス被覆の大きさ})$$

が成り立つ。そのため同じ大きさの独立集合とパス被覆を構築すれば良い。

全ての文字列を反転して trie を構築する。葉ノードには文字列が対応し、しかもどんな文字列の suffix でもないことがわかる。葉ノードの個数を $l$ としよう。

  • 葉ノードに対応する文字列の集合は大きさ $l$ であり、どの二要素も互いに suffix ではない。
  • 葉ノードそれぞれに対して、根ノードから葉ノードに至るまでに出会った $S_1, \ldots, S_N$ の中の文字列をとる (以前取られた文字列は無視する) と、これらの文字列は出会った順にパスをなす。これらのパスはちょうど $l$ 個あり $\lbrace S_1, \ldots, S_N \rbrace$ を被覆する。

よって Dilworth の定理から答えは $l$ である。

(14)

長さNの整数列Aについて、以下の最小化問題と等しい最小化問題は？

「ある要素に+1,または-1する」ことを繰り返してAを広義単調増加にするための、操作回数の最小値

類別: 最小費用流 (MCF) の双対

解法

wata さんのスライドの p.47 を参照する。元の問題は以下のように言い換えられる:

$N$ 個の変数 $X_i$ がある。$X_i \le X_{i+1}$ の条件付きで $\sum_i |X_i - A_i|$ を最小化せよ。

以下のように書き換えることができる。

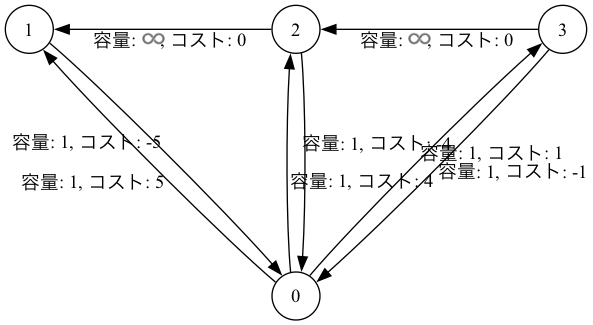
$N + 1$ 個の変数 $X_0, \ldots, X_N$ がある。$\sum_{1 \le i \le N-1} \infty \max(0, X_i - X_{i+1}) + \sum_i 1\max(0, X_i - X_0 - A_i) + \sum_i 1\max(0, X_0 - X_i + A_i)$ を最小化せよ。

これの双対問題はこのようなグラフにおける最小費用流である ($A = [5,4,1]$ の例):

graph.png

さらに言い換えると以下のような問題になる。

長さ $N$ の整数列 $A$ に対して、$\sum_i A[N+1-i]b_i$ を最小化せよ。ただし、

  • $b$ は [-1, 0, 1] のいずれか
  • $\sum_{1 \le i \le N} b_i = 0$
  • $0 \le j \le N$ に対して $\sum_{1 \le i \le j} b_i \ge 0$

この問題は下に凸な折れ線を管理すれば良い。

  • 各 $0 \le k \le N, 0 \le l \le k$ に対して、 $\sum_{1 \le i \le k} b_j = l$ のときの部分和の最小値を $\mathrm{dp}[k][l]$ と呼ぶ。
    • $\mathrm{dp}[k]$ は $l$ の関数として下に凸である。そのため、 $l=0$ から右に見ていくと増分列は単調増加であり、min を取り出せるタイプの優先度キュー + グローバルな差分 で管理できる。
    • 更新時には、「優先度キューに値を 2 回追加」→「グローバルな差分を調整」→「先頭を削除」を行う。
    • Slope Trick と同じ考え方だが、残すのは右側だけで良い。

優先度キューを使えば $O(N \log N)$ 時間で解ける。

コード (Rust) 
use std::cmp::*;
use std::collections::*;

fn getline() -> String {
    let mut ret = String::new();
    std::io::stdin().read_line(&mut ret).ok().unwrap();
    ret
}

fn solve(a: &[i64]) -> Vec<i64> {
    let mut que = BinaryHeap::new();
    let mut global = 0;
    for a in a {
        global -= a;
        que.push(Reverse(a));
        que.push(Reverse(a));
        let Reverse(x) = que.pop().unwrap();
        global += x;
    }
    let v = que.into_sorted_vec();
    let mut ans = vec![global];
    for Reverse(v) in v.into_iter().rev() {
        let new = ans[ans.len() - 1] + v;
        ans.push(new);
    }
    ans
}

fn main() {
    let a: Vec<i64> = getline().trim().split_whitespace()
        .map(|x| x.parse().unwrap())
        .collect::<Vec<_>>();
    a.reverse();
    let ans = solve(&a);
    eprintln!("{:?}", ans);
    println!("{}", -ans[0]);
}
実行結果 
$ rustc sol-14.rs 
$ ./sol-14 <<<"5 4 1"
[-4, 0, 5, 10]
4

(15)

正整数Kについて、以下の最大化問題の答えは？

どの二要素(a,b)についてもa&b < min(a,b)であるような、0以上2^K未満の整数の集合のサイズの最大値

類別: Dilworth の定理

解法

a&b < min(a,b) の否定は a&b == min(a,b) であり、これは a や b を集合とみなしたときに一方が他方の部分集合であることと同値である。

部分集合かどうかの関係は推移的な関係である。よって Dilworth の定理から、

$$(\text{最大独立集合の大きさ}) = (\text{最小パス被覆の大きさ})$$

が成り立つ。そのため同じ大きさの独立集合とパス被覆を構築すれば良い。

レベル $i$ を、 $\lbrace 0, \ldots, K-1\rbrace$ の $i$ 点部分集合全体からなる集合とする。

  • レベル $i$ は独立集合であり、その大きさは $C(K,i)$ である。これの最大値は $i = \lfloor K/2\rfloor$ で実現される。
  • レベル $i$ とレベル $i+1$ でマッチングを作る。正則二部グラフなので必ず小さい方のサイズのマッチングは存在する。そのマッチングを利用してパス被覆を作ると、パス被覆の大きさは最大のレベルの大きさ、つまり $C(K, \lfloor K/2\rfloor)$ である。

よって Dilworth の定理から答えは $C(K, \lfloor K/2\rfloor)$ である。

(16)

整数Xについて、以下の最大化問題と等しい最小化問題は？

Xの最大値

解法

制約がない状態で $1 \cdot X$ を最大化せよという問題。よって双対問題は

$0 = 1$ という条件下で $0$ を最小化せよ

という問題である。これは実行可能解が存在しないので答えは $\infty$ であり、元の問題の答え (際限がないので $\infty$) と等しい。

(17)

各辺に整数重みw[e]が付いたN頂点の平面グラフと、そのある平面埋め込みについて、以下の最小化問題と等しい最大化問題は？

平面上のどの二点も互いに行き来可能にするために、削除する辺の重みの総和の最小値

解法

元の問題は平面グラフの面を頂点とみなした場合の最小全域木を求める問題である。平面グラフの面を頂点とみなした場合の全域木の補集合は平面グラフの全域木であるため、平面グラフの最大全域木を求めれば良い。

(18)

N個の禁止頂点を持つH×Wのグリッドグラフについて、以下の最大化問題と等しい最小化問題は？

(1,1)から(H,W)への内点素なパスの個数の最大値

類別: 最大フロー最小カットの双対

解法

問題は全ての辺の容量が 1 の最大フローとみなすことができる。それの双対は最小カットである。平面グラフの最小カットであるため、平面グラフの面を頂点としてみなして左下 ($(1,1), (H,1), (H,W)$ の外側) と右上 ($(1,1), (1,W), (H,W)$ の外側) までの最短路を求めれば良い。

(19)

H×Wのグリッドがあり、そのうちNマスが黒く塗られている。以下の最小化問題と等しい最大化問題は？

いくつかの行•列を選び、全ての黒いマスが選ばれた行•列の少なくとも一つに含まれているようにするための、選ぶ行•列の総数の最小値

類別: 二部グラフの双対

解法

左に $H$ 頂点、右に $W$ 頂点ある二部グラフを考える。$(i,j)$ にある黒マスを、左の頂点 $i$ と右の頂点 $j$ を結ぶ辺とみなすと、この問題は最小辺被覆である。二部グラフにおける最小辺被覆の双対なので最大マッチングである。

(20)

N頂点の根付き木があり、各頂点には非負整数A[v], B[v]が書かれている。以下の最小化問題と等しい最大化問題は？

いくつかの頂点を選び、任意の頂点vについてその部分木からA[v]個以上が選ばれているようにするとき、選んだ頂点のBの値の和の最小値

類別: 最小費用流 (MCF) の双対

解法

根を頂点 $1$ として良い。 $\sum_{w: v\text{の子孫}} C[w] \ge A[v], C[v] \ge 0$ となる最小の $C$ を計算しておく。元の問題は以下のようなネットワークにおける最小費用流と同値である:

  • 頂点は $N+1$ 個。元々の根付き木の頂点 $1, \ldots, N$ に超頂点 $w$ を加える。
  • 頂点 $i$ の流入は $C[i]$ であり、頂点 $w$ の流入は $-\sum_i C[i]$
  • 親から子に容量 $\infty$ コスト $0$ の辺がある
  • 頂点 $i$ から頂点 $w$ に容量 $1$ コスト $B[i]$ の辺がある
  • 頂点 $w$ から頂点 $1$ に容量 $\infty$ コスト $0$ の辺がある

wata さんのスライドの p.47 によると、これは以下の最小化問題と等価である。

$\min_{p, q} \sum_{i} C[i]p_i - \sum_{i} C[i]q + \sum_{uv: \text{親子}} \infty\max(0, p_v - p_u) + \sum_i \max(0, q - p_i - B[i]) + \infty\max(0, p_1 - q)$

$q \ge p_1, p_u \ge p_v$ が強制されるので、 $q = 0$ としても一般性を失わない。よって以下のようになる:

$p_i \le 0, p_u \ge p_v$ という条件で $\min_{p} \sum_{i} C[i]p_i + \sum_{i} \max(0, - p_i - B[i])$

$p$ の符号を反転させ、式の符号も反転させて最大化問題にすると以下のようになる:

$p_i \ge 0, p_u \le p_v$ という条件で $\max_{p} \sum_{i} C[i]p_i + \sum_{i} \min(0, B[i] - p_i)$

これが際限なく大きくなるのであれば元の問題に実行可能な解が存在しない。

Slope Trick で解けると思われるが未検証。

(21)-(30)

(21)

長さNの整数列Aと整数Kについて、以下の最小化問題と等しい最大化問題は？

A[i]>=Kなるiの最小値

解法

$j \le i$ なら $A[j] < K$ になるような $i$ の最大値

(22)

長さNの正整数列Aと、長さMの1以上N以下の整数列Bについて、以下の存在命題と等しい全称命題は？

N個の容器に対してM回操作を行う。j回目の操作では、N個の容器のうちB[j]個を選び、球を一つずつ入れる。このようにして、最終的に各容器に入っている球の数をA[i]にすることができる。

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

(2) と同じように考察する。同値なフローの問題は以下である:

$N + M$ 頂点のネットワークがあり、頂点 $1 \le i \le N$ の流入は $-A[i]$ であり、頂点 $N+1 \le N+j \le N+M$ の流入は $B[j]$ である。また各ペア $i, j$ に対し、 $N+j$ から $i$ へ容量 $1$ の辺がある。このネットワークでフローを流すのは実行可能である。

流入の和は 0 なので $\sum_i A[i] = \sum_j B[j]$ である。双対問題をとると以下のようになる。

任意の $p, q$ に対して $-\sum_i A[i] p_i + \sum_j B[j] q_j + \sum_{i, j} \max(0, p _ i - q _ j) \ge 0$

ここで、天才考察 (TODO) を行うと、 $p, q$ として考えるべきものはある頂点の部分集合の対 $(S \subseteq \lbrace 1,\ldots, N\rbrace, T \subseteq \lbrace N+1,\ldots, N+M\rbrace)$ の上で $1$、そうでないところで $0$ のものだけであることがわかるので、以下の命題と同値であることが結論できる。

任意の部分集合の対 $(S \subseteq \lbrace 1,\ldots, N\rbrace, T \subseteq \lbrace 1,\ldots, M\rbrace)$ に対し、 $-\sum_{i\in S} A[i] + \sum_{j \in T} B[j] + |S|(M - |T|) \ge 0$

これは $A$ と $B$ をソートすれば $O(|S|\log |S| + |T| \log |T| + |S||T|)$ 時間で検証可能であるし、行列の Monge 性を利用すれば $O(|S|\log |S| + |T| \log |T|)$ 時間で検証可能である。

(23) 未解決

まだ解けていない

(24)

N頂点の森に対して、以下の最大化問題の答えは？

補グラフの最大マッチングのサイズ

意図がわかりかねている

二部グラフの補グラフの最大マッチングの大きさは、

  • 完全二部グラフで左右の頂点数が奇数の場合、 $N/2-1$ (左と右でそれぞれ繋げるだけ繋ぐ)
  • それ以外の場合、 $\lfloor N/2 \rfloor$ (左と右で繋いで、左右繋げるところを繋ぐと最適)

である。森が完全二部グラフとなるのはスターグラフの場合のみであるため、

  • スターグラフで $N$ が偶数の場合、 $N/2-1$
  • それ以外の場合、 $\lfloor N/2 \rfloor$

が答え。

(25)

N頂点のPseudoforestに対して、以下の最大化問題の答えは？

補グラフの最大マッチングのサイズ

(pseudoforest は、連結成分ごとに木 + 1 辺以下であるようなグラフ。連結成分ごとに 辺の本数 <= 頂点数 という条件でも良い)

意図がわかりかねている

(24) と同様に、二部グラフの補グラフの最大マッチングの大きさは、

  • 完全二部グラフで左右の頂点数が奇数の場合、 $N/2-1$ (左と右でそれぞれ繋げるだけ繋ぐ)
  • それ以外の場合、 $\lfloor N/2 \rfloor$ (左と右で繋いで、左右繋げるところを繋ぐと最適)

である。pseudoforest が完全二部グラフとなるのはスターグラフか $2+2$ の完全二部グラフ (大きさ $4$ のサイクル) の場合のみであるため、

  • スターグラフで $N$ が偶数の場合または大きさ $N = 4$ のサイクルの場合、 $N/2-1$
  • それ以外の場合、 $\lfloor N/2 \rfloor$

が答え。

TODO: 奇数サイクルのときになんとかする

(26) 未解決

まだ解けていない

(27)

各頂点に非負整数の重みA[i]が付いたN頂点の無向二部グラフについて、以下の最大化問題と等しい最小化問題は？

頂点の独立集合について、選んだ頂点の重みの最大値

類別: 二部グラフの双対性

解法

左側に $m$ 頂点、右側に $N-m$ 頂点あるとする。元々の問題を式で表現すると以下のようになる。

$0 \le x_i \le 1, 0 \le y_i \le 1$ であり、辺 $uv$ について $x_u + y_v \le 1$ という条件がある。
このとき $\sum_{i}A[i]x_i + \sum_{i}A[m+i]y_i$ の最大値を求めよ。

これの双対は以下のようになる。

辺 $e$ のそれぞれに対して変数 $z_e \ge 0$ がある。。各頂点 $i$ に対して、 $i$ に接続する辺全ての和に対して $\sum z_e \ge A[i]$ という制約がある。 $\sum_e z_e$ の最小値を求めよ。

(28) 未解決

まだ解けていない

(29)

二次元平面上のN個の点(X[i],Y[i])について、以下の最大化問題と等しい最大化問題は？

x1<x2 ∧ y1<y2のとき(x1,y1)から(x2,y2)へ容量1の有向辺を張ったグラフにおける、(-∞,-∞)から(∞,∞)への最大流

意図がわかりかねている

$(-\infty, -\infty) \to (X[i], Y[i]) \to (\infty, \infty)$ と $(-\infty, -\infty) \to (\infty, \infty)$ を流せばよくて、答えは $N+1$ である。

(30)

N頂点の木と，頂点のdisjointな部分集合S,Tに対して，以下の最大化問題と等しい最小化問題は？

Sの頂点とTの頂点を結ぶような，辺素なパス集合のサイズの最大値

類別: 最大フロー最小カットの双対

解法

$S$ や $T$ の頂点を縮約した上で、元々の無向辺を両方向の有向辺にしたグラフにおける最大フロー問題である。よって双対問題は最小カットである。

(31)-(40)

(31) 未解決

まだ解けていない

(32)

二次元平面上の二つの多角形A,Bについて、以下の最大化問題と等しい最小化問題は？

多角形Aをy軸正の方向に動かして行ったとき、多角形Bと接触しないように最大どれだけ動かせるか？

解法

$\min \lbrace x_2 - x_1 \mid (x_1, y) \in A, (x_2, y) \in B, x_1 \le x_2 \rbrace$

(33)

N頂点M辺の辺に重みが付いた有向グラフと、正整数Kに対して、以下の最大化問題と等しい最小化問題は？

「ある辺の重みを1増やし、スコアを1減らす」操作を繰り返した後、スコアに頂点1からNまでの最短距離*Kを足す。スコアの最大値は？

類別: 最小費用流 (MCF) の双対 最短路の双対

解法

wata さんのスライドの p.78 と同様の考察を行う。元の最大化問題は、距離をポテンシャルの差の最大値と捉え直すことによって、以下のように言い換えられる:

$\max_{x} \max_{p} K(p_N - p_1) - \sum_e x_e$ ただし $p_v - p_u \le w_{uv} + x_{uv}$

$x_{uv} = \max(0, p_v - p_u - w_{uv})$ に注意すると、これは以下のように書き換えられる:

$\max_{p} K(p_N - p_1) - \sum_{uv} \max(0, p_v - p_u - w_{uv})$

これを $-1$ 倍して双対をとると以下の問題である。

$N$ 頂点のネットワークがあり、頂点 1 への流入は $K$、頂点 N への流入は $-K$ である。

  • 元々の辺 $uv$ に対して、$u$ から $v$ へ容量 $1$ コスト $w_{uv}$ の辺がある。

このネットワークにおける最小費用流を求めよ。

類題: Longest Shortest Path (JAG Asia 2015)

(34)

N頂点M辺の辺に重みが付いた有向グラフがある。以下の最小化問題と等しい最小化問題は？

各頂点にポテンシャルp[v]を設定したとき、各辺(u,v,w)について|(p[v]-p[u])-w|のペナルティを受ける。ペナルティの総和の最小値

類別: 最小費用流 (MCF) の双対

解法

wata さんのスライドの p.47 を参照する。元の問題は以下のように書き換えることができる。

$\sum_{(u,v,w)} 1 \max(0, p[v] - p[u] - w) + \sum_{(u,v,w)} 1\max(0, p[u] - p[v] + w)$ を最小化せよ。

これの双対問題は以下のようなグラフにおける最小費用流である:

  • 頂点: 元のグラフと同じ
  • 辺: 元のグラフの辺 $(u,v,w)$ に対して、 $u$ から $v$ に容量 $1$ コスト $w$ の辺と、 $v$ から $u$ に容量 $1$ コスト $-w$ の辺

(35)

N個の重みが付いた区間(l,r,w)があり、l,rはそれぞれ単調増加である。以下の最大化問題と等しい最小化問題は？

disjointな区間の集合の重みの和の最大値

類別: 最短路の双対

解法

$l$ から $r$ に重み $-w$ の辺を、$i$ から $i+1$ に重み $0$ の辺を張ったときの、左端から右端までの距離

(36)

長さNの数列Xに対して、以下の最小化問題と等しい最小化問題は？

長さNの数列Aについて、Aを昇順に並べた数列をBとして、Σ_i (-N+2i)*B[i]+Σ_i |A[i]-X[i]|+Σ_i |A[i]-A[i+1]| の最小値

類別: 最小費用流 (MCF) の双対

解法

(2) と同じ方法で考察する。 $\sum 2iB[i]$ の部分を $A[i]$ の線型結合・区間凸関数の和で表せたら勝ち。

$\sum 2iB[i] = \sum 2iA[i] + \sum_{i < j} 2\max(0, A[i] - A[j])$ である。証明は A のバブルソートの過程をなぞり、 $A[i] > A[i+1]$ のときに入れ替えで右辺の値が変わらないこと、最終的に左辺と右辺が同じ値であることを示せば良い。$i,i+1$ を入れ替えると右辺の増分は $2i(A[i+1] - A[i]) + 2(i+1)(A[i] - A[i+1]) - 2\max(0, A[i] - A[i+1]) = 0$ である。

(37)

N頂点M辺のグラフがある。各頂点には白か黒を割り当てるが、いくつかは既に決まっている。以下の最小化問題と等しい最大化問題は？

両端点の色が異なるような辺の数の最小値

類別: 最大フロー最小カットの双対

解法

元の問題は以下のようなグラフにおける最小 $s$-$t$ カットである:

  • 頂点: 元のグラフの頂点に $s$, $t$ の $2$ 頂点を加えたもの
  • 辺: 元のグラフの辺 $uv$ に対して、 $u \to v$ と $v \to u$ のそれぞれに重み $1$ の辺。さらに、 $s$ から白と決まっている頂点に重み $\infty$ の、黒と決まっている頂点から $t$ に重み $\infty$ の辺。

最大フロー最小カット定理から、元の問題の解はこのグラフにおける最大の $s \to t$ フローの流量に等しい。

(38)

N頂点M超辺の超グラフがある。各頂点には白か黒を割り当てるが、いくつかは既に決まっている。以下の最小化問題と等しい最大化問題は？

結んでいる頂点の色が単一でないような超辺の数の最小値

類別: 最大フロー最小カットの双対

解法

超辺 $e = \lbrace x_1, \ldots, x_k\rbrace$ に対して以下のような追加の頂点と辺を作る: (参考: https://theory-and-me.hatenablog.com/entry/2020/03/17/180157 の 3-4. 4変数以上でグラフ表現できる関数)

  • 頂点 $u_e$, $v_e$
  • $u_e \to x_i \to v_e$ に容量 $1$ の辺 ($i = 1, \ldots, k$)
  • $s \to u_e, v_e \to t$ に容量 $1$ の辺

この部分のカットの大きさは $e$ の色が全部同じときに $1$ で、違う色があるときに $2$ である。

最大フロー最小カット定理から、元の問題の解は (このグラフにおける最大の $s \to t$ フローの流量) - (元のグラフの超辺の本数) に等しい。

(39) 未解決

まだ解けていない

(40) 未解決

まだ解けていない

(41)-(50)

(41) 未解決

まだ解けていない

(42) 未解決

まだ解けていない

(43) 未解決

まだ解けていない

(44) 未解決

まだ解けていない

(45) 未解決

まだ解けていない

(46) 未解決

まだ解けていない

(47)

長さNの0,1からなる列A,Bについて，以下の存在命題と等しい全称命題は？

01を10に置き換える操作を繰り返して，AをBに一致させることができる

類別: 最小費用流 (MCF) の双対 フローの実行可能性の双対

解法

(2) と同じように考察する。元の命題は以下のように言い換えられる (0 を右に流すイメージ):

$N$ 頂点のネットワークがあり、頂点 $i$ の流入は $B[i] - A[i]$ である。また頂点 $i$ から頂点 $i+1$ へ、容量 $\infty$ の辺がある。このネットワークでフローを流すのは実行可能である。

流入の和は 0 なので $\sum_i A[i] = \sum_i B[i]$ である。双対問題をとると以下のようになる。

任意の $p$ に対して $\sum_i (B[i] - A[i]) p_i + \sum_{1 \le i \le N-1} \infty\max(0, p _ {i+1} - p _ i) \le 0$

ここで、天才考察 (TODO) を行うと、 $p$ として考えるべきものはある $l$ に対して $p_i = 1 (i \ge l), p_i = 0 (i <> l)$ という形のものだけであることがわかるので、以下の命題と同値であることが結論できる。

$\sum_i A[i] = \sum_i B[i]$ かつ 任意の $l$ に対して $\sum_{i \ge l} (B[i] - A[i]) \le 0$

(48) 未解決

まだ解けていない

(49) 未解決

まだ解けていない

(50)

'a','b','c'からなる長さNの文字列S,Tについて，以下の存在命題と等しい全称命題は？

"abc"を"bca"に，"bca" を "cab" に，"cab" を "abc" に置き換える操作を繰り返して，SをTに一致させることができる

意図がわかりかねている

https://atcoder.jp/contests/agc055/tasks/agc055_b そのままである。mod 3 で見て $i$ 文字目を $S[i+1]- i$ とする (例: b - 2 = c) ことで、以下のような操作にできる。

  • 操作: $S[i] = S[i+1] = S[i+2]$ のときに、 $S[i..i+3] += 1$ を行う。

ここから、 $f(S)$ を、 $S$ に 3 文字連続で同じ文字がある時に貪欲に取り除いたものと定義すると、 $f(S) = f(T)$ が必要十分条件であることがわかる。ただ、何が双対なのかは謎。

類題: https://atcoder.jp/contests/agc055/tasks/agc055_b

(51)-(52)

(51) 未解決

まだ解けていない

(2) と同じように考察する。同値なフローの問題は以下である:

TODO

流入の和は 0 なので TODO である。双対問題をとると以下のようになる。

TODO

参考:

(52)

長さNの正整数列 A と正整数 K について，以下の存在命題と等しい全称命題は？

「A[i] > A[j] なる (i,j) を選び，A[i]-=A[j]とする」操作を繰り返して，すべての要素を K の倍数にできる．

意図がわかりかねている

$A[i]$ がすべて $K$ の倍数であるのと同値。

0
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?