More than 1 year has passed since last update.

約数関数の上限評価に関するアプローチ

Last updated at 2023-11-20Posted at 2023-11-20

約数関数の上限が示せればリーマン予想が証明できるらしい　ということで、面白そうなアイデアが浮かんだので無謀にも色々やってみた結果を残してみる。

結論

（当然ながら）証明には至らず。結果的に、既知の同値な（？）素数密度の問題に帰着した。整数論的なアプローチだと、どう頑張っても素数密度に帰着しそう。
参考：
https://www.sci.kyushu-u.ac.jp/koho/qrinews/qrinews_200309.html

1.導入

【¹】によると、下記式の成立がリーマン予想と同値

$$\frac{\sigma(N)}{N}\leq e^\gamma \ln \ln N\ \ (\text{for all} \ N\geq 5041)$$

ここで、$\sigma$ は約数関数(sum of divisors function).
(例えば $6$の約数は1,2,3,6であり、$\sigma(6)=1+2+3+6=12$).
$\gamma = 0.5772156649...$ はオイラーのガンマ定数(Euler-Mascheroni constant).

$p_i$を素数、$b_i$を非負整数とすれば、$\sigma$は下記の性質を持つ。
$$\sigma(p_1^{b_1}p_2^{b_2}\cdots p_L^{b_L})=\frac{p_1^{b_1+1}-1}{p_1-1}\frac{p_2^{b_2+1}-1}{p_2-1}\cdots \frac{p_L^{b_L+1}-1}{p_L-1}$$

$p_i$を$i$番目の素数として$N$を素数の積で表せば、
$$\sigma(N)=\prod_{i=1}^L\frac{p_i^{b_i+1}-1}{p_i-1}\ \ \ \ \ \cdots(1)$$

1.1.戦略

$N$を固定して $b_i(\geq 0)$を整数に限定せずに数列$\{b_i\}$に自由度を持たせ、$\sigma(N)$の上限値を考える。

1.2.不変値の導入

$$b_i = a_i \log_{p_i} N$$
となるように$a_i$を導入し、

$$N=\prod_{i=1}^L p_i^{b_i}=\prod_{i=1}^L p_i^{a_i \log_{p_i} N}=\prod_{i=1}^L N^{a_i}=N^{\sum_{i=1}^L a_i}$$

と書き直すと、$a_i$の総和は 1 となる制約を導入できる。
$$\sum_{i=1}^L a_i \ = \ 1$$
非負の実数列$\{b_i\}$に対して式(1)に当てはめたものを$\sigma$と区別して$\hat{\sigma}(N)$と書くことにする。

$$\hat{\sigma}(N) := \prod_{i=1}^L\frac{p_i^{b_i+1}-1}{p_i-1}=\prod_{i=1}^L p_i^{b_i}\frac{1-p_i^{-b_i-1}}{1-p_i^{-1}}=N\prod_{i=1}^L\frac{1-p_i^{-b_i-1}}{1-p_i^{-1}}$$

以降、$\hat{\sigma}(N)\geq \sigma(N)$を保証できるように$\{b_i\}$(もしくは$\{a_i\}$)を選ぶ。

2. hat{σ}(N)を最大にするa_iを導出する

適当な定数$c(>0)$で $a_i+a_j=c$に固定したとき、$x=a_i$と置いて、$\hat{\sigma}(N)$が最大となる$x$を導出する。
式を簡略化するため暫定的に$p:=p_i$, $q:=p_j$と表記する。
$\hat{\sigma}(N)/N$の$i,j$番目の項だけが可変であるとして、その積を求めると

$$\frac{1-p^{-x\log_p N-1}}{1-p^{-1}}\frac{1-q^{-(c-x)\log_q N-1}}{1-q^{-1}}= \frac{(1-p^{-1}N^{-x})(1-q^{-1}N^{x-c})}{(1-p^{-1})(1-q^{-1})}$$

これを$x$について微分する前に、$x$に対して固定値となる分母をはらい、さらに微分した式が簡単となるように$\ln N$で割った下記の関数を考える。
$$f(x) := (1-p^{-1}N^{-x})(1-q^{-1}N^{x-c})/\ln N$$

微分すると下記を得る。
$$f'(x)=p^{-1}N^{-x}-q^{-1}N^{x-c}$$
さらに微分すると、
$$f''(x) = -(p^{-1}N^{-x}+q^{-1}N^{x-c})\ln N <0$$
であり、関数$f$は上に凸である。

$f'(x)=0$
⇔ $p^{-1}N^{-x}=q^{-1}N^{x-c}$
⇔ $N^{2x}=N^c p^{-1}q$
⇔ $x=\frac{c}{2}+\frac{1}{2}\log_N\frac{q}{p}$
⇔ $x=\frac{c}{2}+\frac{1}{2}(\log_N q - \log_N p)$

$$x_0 := \frac{c}{2}+\frac{1}{2}(\log_N q - \log_N p)$$
とすれば、
$0\leq x_0\leq c$ (つまり $-c\leq \log_N(q/p)\leq c$ )のとき、$f(x)$ は $x=x_0$ で最大値を取る。

隣り合う要素間を考え、$j=i+1$として、この組に対する$c$を$c_i$としたとき、
$$a_i = \frac{c_i}{2}+\frac{\log_N p_{i+1} - \log_N p_i }{2} $$
$$a_{i+1} = \frac{c_i}{2}-\frac{\log_N p_{i+1} - \log_N p_i }{2}$$
と書けて、シンプルな式
$$a_{i}-a_{i+1} = \log_N p_{i+1} - \log_N p_i \ \ \ \ \cdots(2)$$
が得られる。

これを$i=1,2,3,...$と適用していくと
$$a_i = a_1 - (\log_N p_i - \log_N 2) $$
を得る。

$\{a_i\}$は単調減少であるほうが$\hat{\sigma}(N)$を大きくできると言える。ただし$a_{i+1}\geq 0$。および$\sum_{i=1}^k a_i\leq 1$が制約となる。

2.1. hat{σ}(N)の評価

ここで得た$\{a_i\}$は
$$\frac{\hat{\sigma}(N)}{N}> e^\gamma \ln \ln N$$
となってしまうことが確認できたため、次章で$b_i$に対する制約を導入することにした。

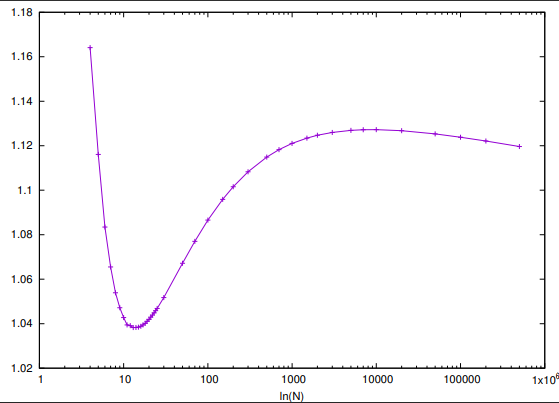
下図は $\hat{\sigma}(N)/(e^\gamma N\ln \ln N)$をプロットしたもの

1を超えてしまっている。

3. b_iの下限の導入

$0<b_i<1$は$\sigma(N)$の計算において使用されないため、$\hat{\sigma}(N)$の計算においても$0<b_i<1$の使用を避けても$\hat{\sigma}(N)\geq \sigma(N)$とできる。

3.1. b_iの単調性

$\hat{\sigma}(N)$を最大化するためには、「$b_i=0$かつ$b_{i+1}=1$」よりも「$b_i=1$かつ$b_{i+1}=0$」とするほうが「有利」($\hat{\sigma}(N)$を大きくできる)であることを直感的な方法で示す。

$b_i$(または$a_i$)を変化させることを考える。
値$a_i$を増加させる量を「消費」(consume)、$\hat{\sigma(N)}/N$の増加比を「寄与」(contribute)と表現することにする。
・$b_i$を$0\to 1$とする操作は、消費が$\log_N p_i$、
・$b_{i+1}$を$0\to 1$とする操作は、消費が$\log_N p_{i+1}$
つまり、消費は$b_{i+1}$を$0\to 1$に変化させるほうが$b_i$に対する同じ操作よりも大きい。
対して、
・$b_i$を$0\to 1$とする操作は、寄与が$1+p_i^{-1}$
・$b_{i+1}$を$0\to 1$とする操作は、寄与が$1+p_{i+1}^{-1}$
であり、寄与は$b_{i+1}$を$0\to 1$に変化させるほうが$b_i$に対する同じ操作よりも小さい。
従って、$b_{i+1}$を$0\to 1$とするよりも$b_i$を$0\to 1$とするほうが有利である。

3.2. 数列の長さLの上限

以降の式を簡素に記述するため、下記の記号を導入する。
$$T(i):=\sum_{j=1}^i \ln p_j $$
$$T_N(i):=\sum_{j=1}^i \log_N p_j $$

$\{a_i\}$（もしくは$\{b_i\}$）の要素数$L$は、$\forall i\ \ b_i\geq 1$の制約のもとで、

$$1=\sum_{i=1}^L a_i = \sum_{i=1}^L b_i \frac{\ln p_i}{\ln N}\ \geq \ \sum_{i=1}^L \frac{\ln p_i}{\ln N} =\frac{1}{\ln N}T(L)$$
であるから、
$$T(L) \leq \ln N $$
を得る。

なお、【²】の式(3.14), (3.15)より、

$$ | T(L)-p_L | \ < \ \frac{p_L}{2\ln p_L} \ \ \ (p_L\geq 563) $$

4. 合わせ技

パラメータ $K$ を導入し、$K<i\leq L$に対して$b_i=1$とする。

a_i=\left\{\begin{array}{ll}
a_1-(\log_N p_i-\log_N p_1)  & (i\leq K)\\
     \log_N p_i & (K<i\leq L)\
\end{array}\right.

(2)を繰り返し適用して式変形すると

a_i=\left\{\begin{array}{ll}
a_K-(\log_N p_i-\log_N p_K) & (i\leq K)\\
     \log_N p_i & (K<i\leq L)\
\end{array}\right.

（$b_i\geq 1$かつ$\sum_{i=1}^L a_i=1$の制約のもとで、）上記の数列の取り方をしたときに唯一の可変なパラメータは$K$であるとして考えると、 $\hat{\sigma}(N)$を最大化する$K$は下記を満たす必要がある。
$$ a_K-a_{K+1} \leq \log_N p_{K+1} - \log_N p_{K} \ \ \ \cdots(3)$$
（この式を満たさないのであれば、式(2)による値の配分余地があり、$a_{K+1}$を増加させて$\hat{\sigma}(N)$を増加可能である。）

4.1. Kの最大化

$a_K$を導出することを考える。$b_K=1\ (a_K=\log_N p_K)$に対する$a_K$のオフセットを$r$とおく。つまり、
$$ r:= a_K - \log_N p_K \ \ (\geq 0)$$
とする。

式(3)より、
$a_K-a_{K+1} \leq \log_N p_{K+1} - \log_N p_K $
⇔ $(r + \log_N p_k) - \log_N p_{k+1} \leq \log_N p_{K+1} - \log_N p_K $
従って、
$$ r \leq 2\log_N p_{K+1} - 2\log_N p_K \ \ \ \cdots(4)$$

$1=\sum_{i=1}^L a_i$を面積に見立てて3つの部分に分割する。

$rK$・・・$a_i\ (i\leq K)$のオフセット部分の面積
$S_1(K)$・・・$a_i\ (i\leq K)$からオフセット部分を除外した部分の面積
$S_2(K,L)$・・・残りの部分の面積（$a_i\ (K<i\leq L)$の総和）

$1=rK+S_1(K)+S_2(K,L)$である。

\displaylines{
S_1(K) = \sum_{i=1}^K (a_i-r) \\
     = \sum_{i=1}^K (a_K-(\log_N p_i-\log_N p_K)) \ -\ rK \\
     = K a_K - T_N(K) + K \log_N p_K -K(a_K - \log_N p_k) \\
     =     2K \log_N p_K  - T_N(K)
}

$$S_2(K,L) = \sum_{i=K+1}^{L} a_i = \sum_{i=K+1}^{L} \log_N p_i = T_N(L) - T_N(K) \label{eq_b_eq_1_a_kp1_to_l}$$

$rK= 1 - S_1(K) - S_2(K,L) = 1 - 2K \log_N p_K + 2T_N(K) - T_N(L)$
⇔ $r = \frac{1}{K}(1 - (2K \log_N p_K - 2T_N(K) + T_N(L)))$
⇔ $r\ln N = \frac{1}{K}(\ln N - (2K \ln p_K - 2T(K) + T(L)))$

式(4)より、$ \ln N\ - (2K \ln p_K - 2T(K) + T(L)) \ \leq\ 2K\ln p_{K+1} - 2K\ln p_K $
⇔ $ \ln N\ - T(L) \ \leq\ 2K\ln p_{K+1} - 2T(K)$

これで、$L$を決めれば$K$が決まる。

5. hat{σ}(N)の最大化

$\hat{\sigma}(N)$を最大化する$L$の導出については数式を導出できなかったため、コンピュータにより最大値を探索してプロットすることにした。

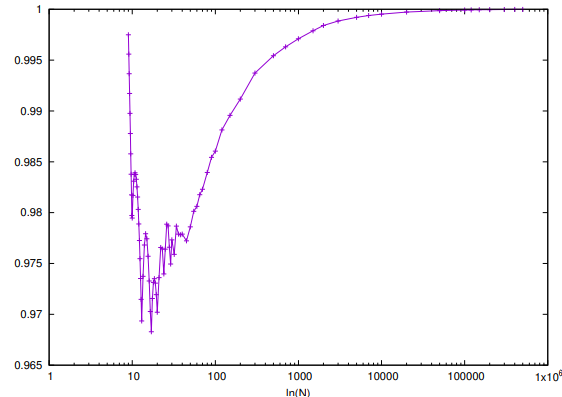
下図はこの$a_i$の選び方で $\hat{\sigma}(N)/(e^\gamma N\ln \ln N)$をプロットしたもの

プロットした範囲$\ln N\leq 10^6$では1を下回っているが、$N$をさらに大きくすると1を超える。

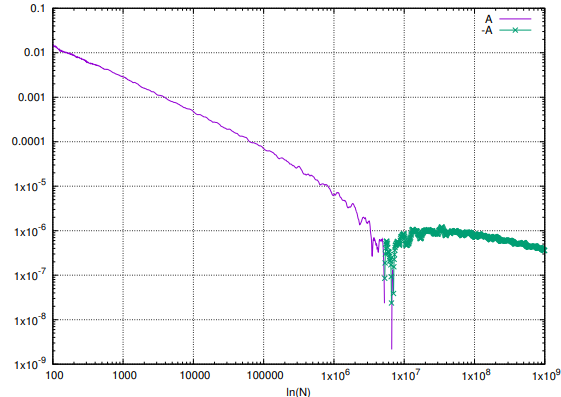
下図中で、$A:=1\ -\ \hat{\sigma}(N)/(e^\gamma N\ln\ln N)$.
緑のプロットは$-A$であり、$\hat{\sigma}(N)>e^\gamma N\ln\ln N$となっていることを表している。

6. 諦めるにはまだ早い（？）

【³】(【²】で引用されている)によると、

If the Riemann hypothesis is false, then there exist constants $0<\beta<\frac{1}{2}$ and $C > 0$ such that
$$\sigma(N)/N \geq e^\gamma \ln \ln N +\frac{C \ln \ln N}{(\ln N)^\beta}$$
holds for infinitely many $N$

とのことなので、$e^\gamma \ln N \ln N$を上回っている$\hat{\sigma}(N)/N$が存在しても、その差の上限が
$$O(\ln \ln N /\sqrt{\ln N})$$
で抑えられればリーマン予想の成立が言えそうである。
ここで、$O$はランダウの記号。

6.1. hat{σ}(N)の上限評価

\displaylines{
    D_1(K) &:= \left(\prod_{i=1}^K(1-p_i^{-1-b_i})\right)^{-1} \\
    D_2(K,L) &:= \left(\prod_{i=K+1}^L(1-p_i^{-2})\right)^{-1} \\
    D_3(L) &:= \left(\prod_{i=1}^L(1-p_i^{-1})\right)^{-1}
}

とおくと、

\displaylines{
    \ln \hat{\sigma}(N)-\ln N
    = \sum_{i=1}^K \ln(1-p_i^{-1-b_i}) \ + \ \sum_{i=K+1}^L \ln(1-p_i^{-1-b_i}) - \sum_{i=1}^L \ln(1-p_i^{-1}) \\
    = -\ \ln D_1(K) \ - \ \ln D_2(K,L) \ + \ \ln D_3(L) \ \ \ \cdots (5)
}

6.1.1. D_1の範囲の導出

\begin{align}
\ln D_1(K) 
    &= -\sum_{i=1}^K \ln(1-p_i^{-1}p_i^{-a_i\log_{p_i}N}) \\
    &= -\sum_{i=1}^K \ln(1-p_i^{-1}N^{-a_i})  \\
    &= -\sum_{i=1}^K \ln(1-p_i^{-1}N^{-a_K+\log_N p_i-\log_N p_K})  \\
    &= -\sum_{i=1}^K \ln(1-N^{-a_K}p_K^{-1})  \\
    &= -K\ln(1-N^{-a_K}p_K^{-1}) \\
    &= -K\ln(1-N^{-r-\log_N p_K}p_K^{-1}) \\
    &= -K\ln(1-N^{-r}p_K^{-2})
\end{align}

$r$の範囲から下記が得られる。

$$ -K\ln(1-p_{K+1}^{-2}) \leq \ln D_1(K) \leq -K\ln(1-p_K^{-2}) $$

6.1.2. D_2の範囲の導出

省略

6.1.3. D_3の範囲の導出

$f(x):=-\ln(1-x^{-1})$とおいて、【²】の式(2.26)を適用する。
ここで、$\text{li}(x)$は対数積分、$\pi(x)$は素数個数関数をあらわす。
下記は $F_3(p_i) = \ln D_3(i)$に相当する。

\begin{align}
    F_3(x):= & \sum_{p\leq x} (-\ln(1-p^{-1})) \\
         = &  \int_2^x \frac{f(y)}{\ln y}dy +f(2)\text{li}(2) \\
           & -\int_2^x f'(y)(\pi(y)-\text{li}(y)) dy + f(x)(\pi(x)-\text{li}(x)) \\
         = & -\int_2^x \frac{\ln(1-y^{-1})}{\ln y}dy -\text{li}(2)\ln 2 \\
           & +\int_2^x \frac{\pi(y)-\text{li}(y)}{y(y-1)} dy - \ln(1-x^{-1})(\pi(x)-\text{li}(x)) \\
         = & H_{31}(x) + H_{32}(x) + H_{33}(x) + H_{34}(x)
\end{align}

ここで

\begin{align}
    H_{31}(x) &:= -\int_2^x \frac{\ln(1-y^{-1})}{\ln y}dy \\
    H_{32}(x) &:= -\text{li}(2)\ln 2 \\
    H_{33}(x) &:= \int_2^x \frac{\pi(y)-\text{li}(y)}{y(y-1)}dy \\
    H_{34}(x) &:= - \ln(1-x^{-1})(\pi(x)-\text{li}(x))
\end{align}

$H_{31}(x)$, $H_{34}(x)$ に対してテーラー展開を適用し、
$$ -\ln(1-x^{-1}) = x^{-1} + R_3(x)x^{-2} \ \ (R_3(x) \simeq 1/2)$$

\begin{align}
   H_{31}(x) &= \int_2^x \frac{1}{y\ln y}dy + \int_2^x \frac{R(y)}{y^2\ln y}dy \\
          &= \int_2^x ((\ln\ln y)^{-1})' dy + \int_2^x \frac{R(y)}{y^2\ln y}dy \\
          &= \ln\ln x - \ln\ln 2 + \int_2^\infty \frac{R(y)}{y^2\ln y}dy - \int_x^\infty \frac{R(y)}{y^2\ln y}dy \\
          &= \ln\ln x + C_{31} + G_{31}(x) \\
   H_{32}(x) &= -\text{li}(2)\ln 2 =: C_{32} \\
   H_{33}(x) &= \int_2^\infty \frac{\pi(y)-\text{li}(y)}{y(y-1)} dy - \int_x^\infty \frac{\pi(y)-\text{li}(y)}{y(y-1)} dy \\
          &= C_{33} + G_{33}(x) \\
   H_{34}(x) &= x^{-1}(1+R(x)x^{-1})(\pi(x)-\text{li}(x)) =: G_{34}(x)
\end{align}

定数部分を$C_{31},C_{32},C_{33}$とおき、残りの部分
$G_{31}(x),G_{33}(x),G_{34}(x)$ を

\begin{align}
    G_{31} &:= -\int_x^\infty \frac{R(y)}{y^2\ln y}dy \\
    G_{33} &:= -\int_x^\infty \frac{\pi(y)-\text{li}(y)}{y(y-1)} dy \\
    G_{34} & = \text{上述のため省略}
\end{align}

とおくと、

\begin{align}
    \lim_{x \rightarrow \infty }G_{31}(x) = 0 \\
    \lim_{x \rightarrow \infty }G_{33}(x) = 0 \\
    \lim_{x \rightarrow \infty }G_{34}(x) = 0
\end{align}

となる。（厳密には収束性の議論が必要。）

$$F_3(x) = \ln\ln x \ + \ C_{31}+C_{32}+C_{33} + G_{31}(x)+G_{33}(x)+G_{34}(x)$$
と書ける。

【²】の式(3.28)、式(3.29)より
$$ 1-\frac{1}{(2\ln x)^2} < (e^\gamma \ln x)^{-1}\prod_{p\leq x} (1-p^{-1})^{-1} < 1+\frac{1}{(2\ln x)^2}\ \ \ (x\geq 286)$$

対数をとると
$$ \lim_{x\rightarrow \infty} \left( F_3(x) - \ln\ln x \right) = \gamma$$
となり、
$$ F_3(x) = \ln\ln x + \ \gamma \ + G_{31}(x)+G_{33}(x)+G_{34}(x)$$
を得る。

7. 結論

$|G_{33}|$（および$|G_{34}|$）の上限評価が、リーマン予想に帰結する素数密度の問題
$$|\text{li}(x)-\pi(x)|<O(\sqrt{x}\ln x) \ \ \text{が真かどうか}$$
に直結していそうで、（粗く表現すると、）証明が循環参照状態となり、断念。。

7.1. 蛇足

「3.2. 数列の長さ$L$の上限」で、式(5)の$L$が$p_L\simeq \ln N$であるが、
$D_1$と$D_2$で$D_3$を打ち消しあわせて$L$を削るようにして上限値を抑え込めないか考えてみたが、ダメそう。

An Elementary Problem Equivalent to the Riemann Hypothesis
Jeffrey C. Lagarias (May 5, 2001 version) ↩
APPROXIMATE FORMULAS FOR SOME FUNCTIONS OF PRIME NUMBERS BY J. BARKLEY ROSSER AND LOWELL SCHOENFELD ↩ ↩² ↩³ ↩⁴
G. Robin, Grandes valeurs de la fonction somme des diviseurs et hypoth`ese de Riemann, J. Math. Pures Appl. 63 (1984), 187–213. ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up