rotationプロパティでの回転は、X,Y,Z軸について各1回しか回転させることができないので、複数回回転させる場合は、Matrixを使って回転させるのが楽。
See the Pen RotateByUsingApplyMatrix_ThreeJs by kob58im (@kob58im) on CodePen.
【追加】箱を転がしてみる
R,G,B(赤,緑,青)がそれぞれX,Y,Z軸
See the Pen RollingBox-ThreeJs by kob58im (@kob58im) on CodePen.
回転軸をずらしてみた。
解説
前提:
geometry(≒3Dオブジェクトの頂点の集合)に対する回転処理に関しては、positionは影響しないようである。(console.log(box.position.x)で出力した値が変化しなかった。)
なので、positionは無視して考えてよい。
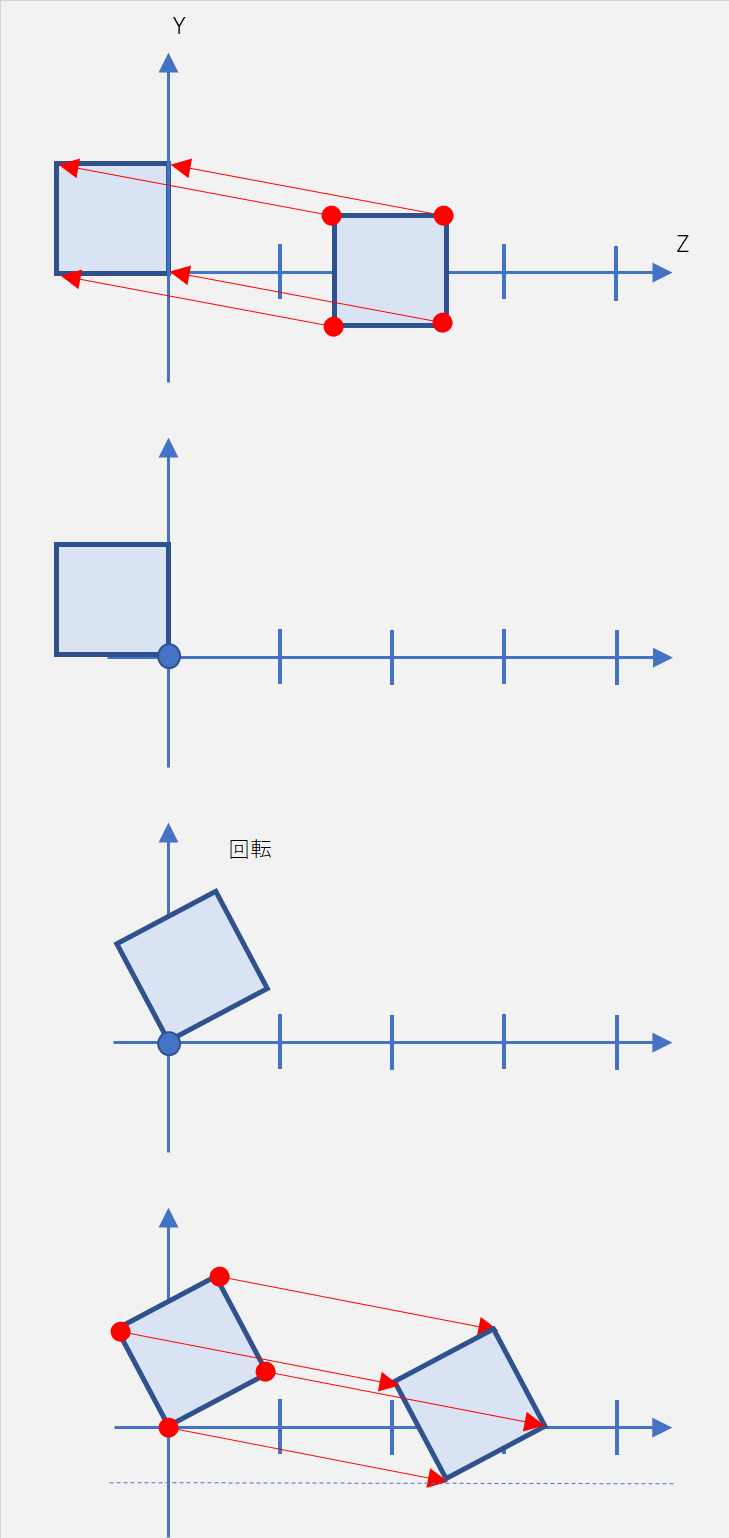
X軸方向を回転軸として回転させているところの処理を図解してみる。
function rotX(degX) {
let signDegX = (degX<0)?1:0;
let mat;
mat = new THREE.Matrix4().makeTranslation( 0, boxSize/2, -boxSize*(1/2 + boardZpos - signDegX) );
box.geometry.applyMatrix(mat);
mat.makeRotationFromEuler(new THREE.Euler( Math.PI*degX/180, 0, 0, 'XYZ' ));
box.geometry.applyMatrix(mat);
mat = new THREE.Matrix4().makeTranslation( 0, -boxSize/2, boxSize*(1/2 + boardZpos - signDegX) );
box.geometry.applyMatrix(mat);
redraw();
}
簡単のため、例として、boxSize=1,degX>0, boardZpos=2とした場合で考える。(下記)
function rotX(degX) {
let mat;
mat = new THREE.Matrix4().makeTranslation( 0, 1/2, -(1/2 + 2) );
box.geometry.applyMatrix(mat); // 回転軸にしたい頂点が原点にくるように平行移動
mat.makeRotationFromEuler(new THREE.Euler( Math.PI*degX/180, 0, 0, 'XYZ' ));
box.geometry.applyMatrix(mat); // X軸を回転軸としてで回転
mat = new THREE.Matrix4().makeTranslation( 0, -1/2, (1/2 + 2) );
box.geometry.applyMatrix(mat); // 元の位置に平行移動
redraw();
}
図の点線部分は地面。今回のプログラムでは、yの負方向に埋もれている分をbox.position.y = boxSize/2でオフセットさせてy=0に来るようにしている。