本記事はQrunchに投稿していた記事の再掲になります。
そのため、本記事に類似して且つ詳しい記事がQiita上に存在するかもしれません。
悪しからず。
相関とは
一般的に相関と言われているのは、ピアソンの相関(以下、相関)。
相関は2つのデータの直線的な関連度合いを-1 ~ +1で表す。
相関とは
相関の強さ
以下のコードでは、一次関数に従い乱数を生成している。
グラフのプロットの通り、直線的な関係が見て取れる。
相関係数は0.96なので、かなり強い相関だといえる。
import numpy as np
from matplotlib import pyplot as plt
# 乱数生成
x = np.random.normal(0,1, 1000)
noise = np.random.rand(1000)
y = (x + noise)
# グラフ描画
plt.scatter(x, y)
plt.show()
# 相関係数
print(np.corrcoef(x, y))
# 0.96...

相関のよくある勘違い
繰り返しだが、
相関は2つのデータの直線的な関連度合いを表す。
相関 = 2つのデータの関連度合いというのは間違い。
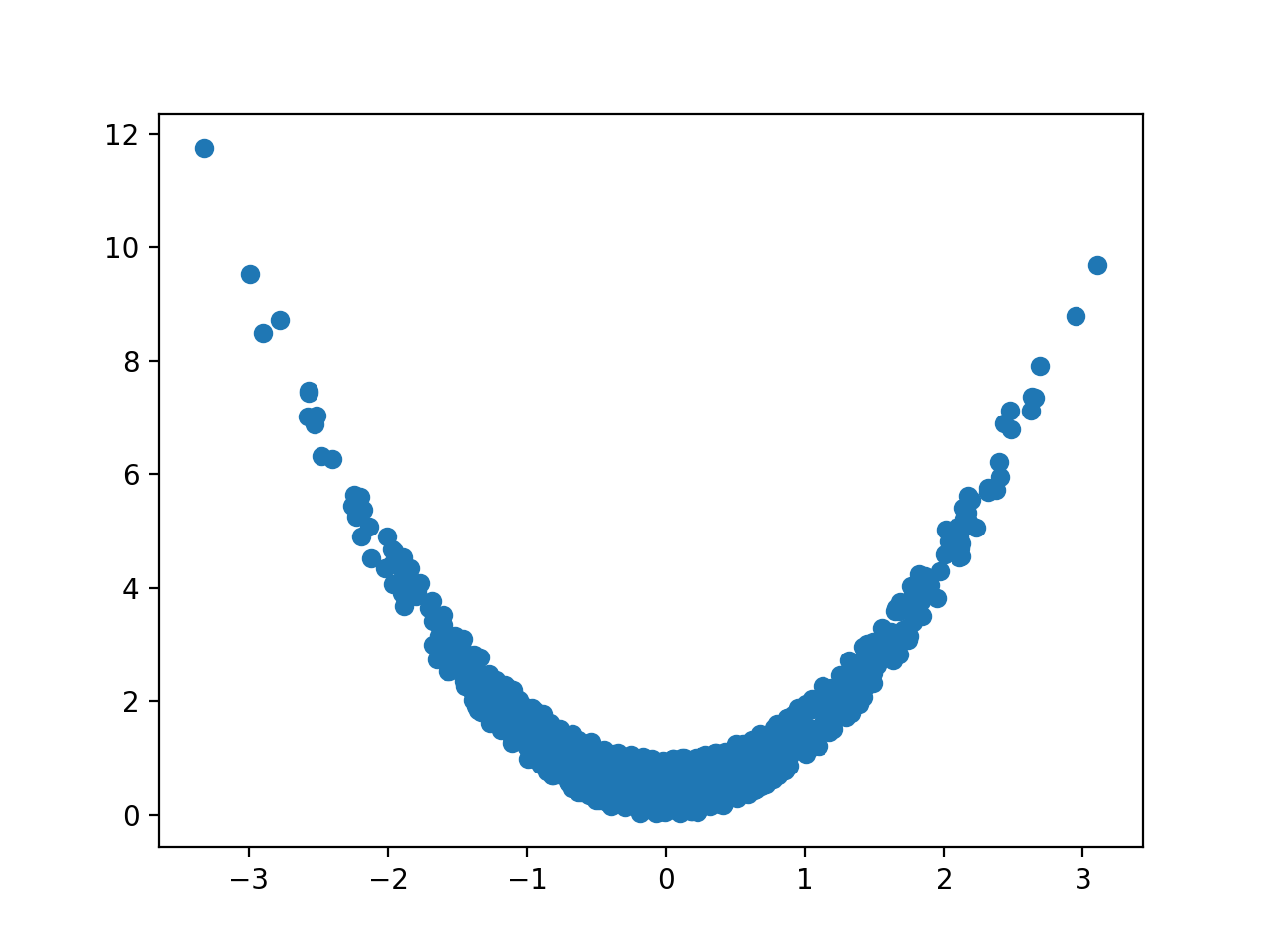
以下のコードでは、二次関数に従い乱数を生成している。
グラフのプロットの通り、直線的ではないが「xとyに関係があること」は見て取れる。
相関関係は0.06だった。
import numpy as np
from matplotlib import pyplot as plt
# 乱数生成
x = np.random.normal(0,1, 1000)
noise = np.random.rand(1000)
y = x**2 + noise
# グラフ描画
plt.scatter(x, y)
plt.show()
# 相関係数
print(np.corrcoef(x, y))
# 0.06...
上述より、「相関係数が0に近い!このデータは関係性がないんだ!」と結論付けるのは危険ということがわかる。
データの関係性を表せる「相関係数」と2つの落とし穴
ちなみに、BMIと死亡リスクのグラフが同じような形らしい。

MIC相関
じゃあどうやって上記のような関連度合いを捉えるのか。
今回はMIC相関を使う。
MIC相関は21世紀に入ってから考案された手法で、
非線形(直線的な関係じゃない)データの関連度合いも数値化できる。
MIC相関はこちらがわかりやすい。
新しい相関係数"MIC"の解説
PythonでMIC相関
Pythonなら簡単にMIC相関が使える。
MIC関数を使うにはminepyが必要。
pip install minepy
上述と同様に、二次関数に従い乱数を生成している。
MIC相関は0.75だった。
このようにMIC相関では非線形(直線的な関係じゃない)データの関連度合いも数値化できる。
import numpy as np
from matplotlib import pyplot as plt
from minepy import MINE
# 乱数生成
x = np.random.normal(0,1, 1000)
noise = np.random.rand(1000)
y = x**2 + noise
# グラフ描画
plt.scatter(x, y)
plt.show()
# MIC相関
mine = MINE()
mine.compute_score(x, y)
print(mine.mic())
# 0.75...
あとがき
MIC相関は手法の特性上ノイズに弱い。
非線形でも関連性を捉えられるが、sin波のように周期的なデータには弱い。