あらすじ
f(x)=\frac{1}{\sqrt{2\piσ^2}}e^{-\frac{(x-μ)^2}{2σ^2}}
正規分布は代表的な分布の一つであり、統計の分野で頻出する分布です。
しかし正規分布の確率密度関数は↑式のようにとてもややこしく、多くの初学者を葬り去ってきました。
かく言う僕も統計の勉強を始めて、初めてこの式を見た時は頭痛と眩暈を覚えた記憶があります。
本記事では、↑式の係数部分($\frac{1}{\sqrt{2\piσ^2}}$)と指数部分($-\frac{(x-μ)^2}{2σ^2}$)に分けて、なぜこのような形になったのかを記述していきます。
指数部分
世の中の多くの事象は平均値を取る確率が最も大きく、平均値から離れるにつれその値を取る確率は小さくなります。
これを簡単に表す式が、
f(x)=e^{-x^2}
です。
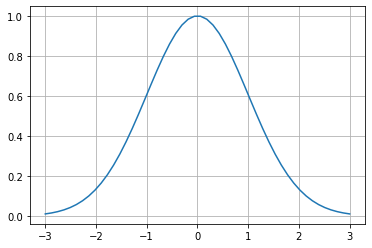
グラフで表すと、
import numpy as np
import matplotlib.pyplot as plt
def normal_dist(x, ave = 0, disp=1):
return np.exp((-(x-ave)**2)/(2*disp**2))
x = np.linspace(-3, 3)
y = normal_dist(x)
plt.plot(x,y)
plt.grid(axis="both")
plt.show()
こんな感じで山なりの形になります。
この式では一通りのグラフしか書けないので汎用性に劣ります。
そこで、
①グラフの左右移動
②グラフ幅の変更
の機能を追加します。
###グラフの左右移動
$x$の部分を$x-μ$に変更することで、極大値を取る$x$の位置をずらすことが出来ます。
f(x)=e^{-(x-μ)^2}
こんな式になります。
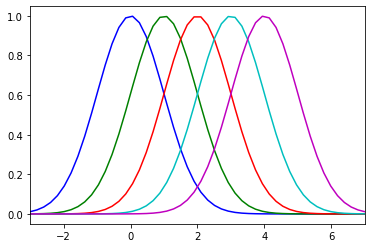
$μ$の値を変えていき、グラフの変化を見てみましょう。
color = ["b", "g", "r", "c", "m"]
for i, col in enumerate(color):
y = normal_dist(x, i)
plt.plot(x, y, color=col)
plt.show()
$μ$が大きくなるにつれ、グラフが右にずれていきました。
###グラフ幅の変更
指数部分に$\frac{1}{2σ^2}$を掛けると幅の変更が可能になります。
f(x)=e^{-\frac{x^2}{2σ^2}}
x = np.linspace(-10, 10)
color = ["b", "g", "r", "c", "m"]
for i, col in enumerate(color):
y = normal_dist(x, 0, i+1)
plt.plot(x, y, color=col)
plt.show()
幅を変えることに成功しました。
σを二乗にしたのは正負どちらも扱えるようにするため、$2$を掛けているのは計算しやすくするためです。
係数部分
確率密度関数なので面積の合計が$1$でなければいけません。
そこで都合の良い値を関数に掛けてやります。
都合の良い係数を$c$と置き、
\int_{-\infty}^{\infty}ce^{-\frac{(x-μ)^2}{2σ^2}}dx=1
を計算し、$c$を求めます。
一見やっかいな計算に見えますが、
\int_{-\infty}^{\infty}e^{-ax^2}dx=\sqrt{\frac{\pi}{a}}
このガウス積分の公式を用いて$a=\frac{1}{2σ^2}$とすれば
c=\frac{1}{\sqrt{2\piσ^2}}
となり、簡単に計算が可能です。
解は一番上の式の係数になりました。
結局この式は、$f(x)=e^{-x^2}$に汎用性を持たせ、係数を調整することで確率密度関数を定義するという式なのでした。
めでたしめでたし。
参考にしたサイト
https://to-kei.net/distribution/normal-distribution/density-function-derivation/
正規分布の密度関数を意味的に理解する
https://mathtrain.jp/gauss
ガウス積分の公式の２通りの証明