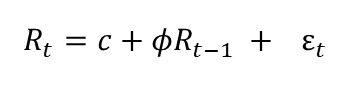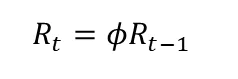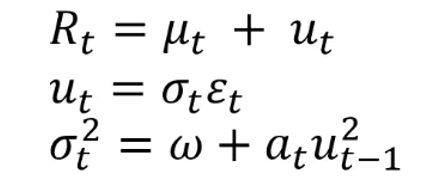導入
時間の経過に伴って変化するデータを示す、時系列データについての記事です。
時系列データは、自然科学、社会科学、経済学、金融、医療、エンジニアリングなど、多くの分野で扱われています。
今回はそんな時系列データを分析する際に出てくるARCHモデルついての説明をします。
この記事では現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~ :横内 大介, 青木 義充 著(2014)のデータを使い、ARCHモデルについてRを使いながら説明していきます。
前提知識として必要な概念
・自己回帰モデル(ARモデル)
・ホワイトノイズ
さらっと解説します
自己回帰モデル
現在の自分を過去の自分で表すモデル式
ARモデルとも呼ばれます。(Auto Regressive model)
一般式はこう
ある時点tでの値を、過去の時点(t-1)の自分で表しています
シンプルな形にするとただの一次式なのでわかりやすいと思います。
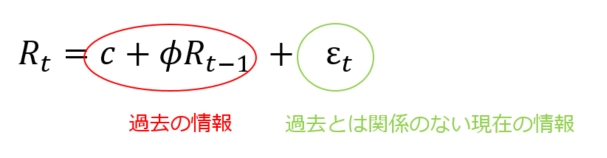
このシンプルな式に
自分以外の過去の情報:C
過去とは無関係な現在の情報ノイズ:ε
を加えると一般式になり__過去の情報__と__現在のノイズ__で__現在の自分を表す__ことができます。
ホワイトノイズ
上で紹介した自己回帰モデルの ε のこと。
特徴はざっくり言うと次の3つです。
1.定常時系列の代表、扱いやすい
2.平均 = 0、分散 = 一定、自己共分散 = 0
3.現在の自分は過去の自分と無関係
自己共分散や定常性については割愛します。
本題に向けて
ホワイトノイズは扱いやすいがこいつだけでなんでもかんでもあてはまりの良い自己回帰モデルを作るには限界がある。
そこで分散不均一構造の代表ARCHモデルの出番、というわけです。
ARCHモデル
分散不均一構造モデルの代表例です
正式名称は自己回帰条件付き分散不均一モデル(Auto Regressive Heteroskedasticity model)
頭文字をとってARCHモデル
ARは自己回帰モデルのARと同じ意味です。
このモデルの意味するところは__前回絶対値の大きなノイズが来たのであれば今回の分散は大きくなるだろう__ということです。
株価を例に考えましょう。
昨日A社の株がすごく下がった(=大きなノイズが来た)
このあとよくある株価の動きは2つです。
1.するとみんなA社の株をたくさん買った(買い時だと思った)
→株価は反発し上がった
2.するとみんなA社の株をたくさん売った(これ以上下がったら嫌だ)
→株価はさらに下がった
この2つに共通しているのが大きなノイズがきたので株価がまた大きく動いたということです.
具体例としてリーマンショックや一時期のビットコインなんかを考えていただければ動くときは一定方向に大きく動くことをイメージしやすいでしょうか。
こういった株価に代表される動きはホワイトノイズで表すことはできませんがARCHモデルによって表すことができます。
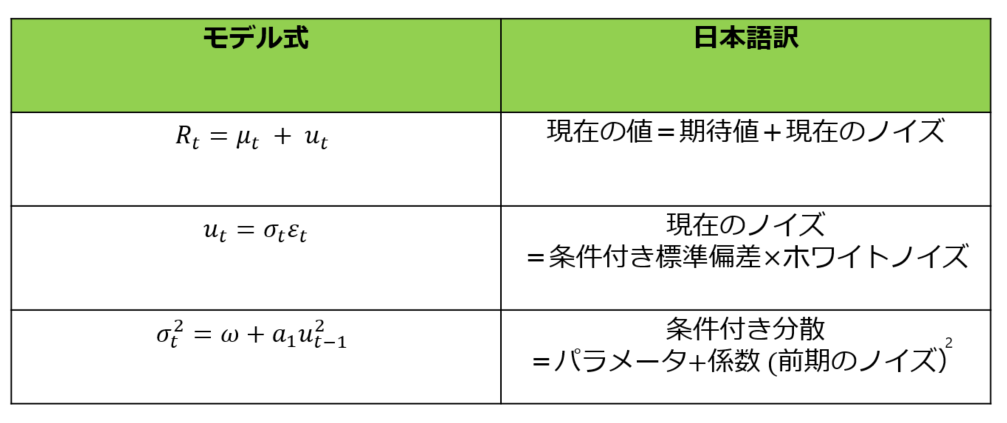
1つ目は自己回帰モデルの式です。
期待値 μt の部分は今までの自己回帰モデル式で言えば c + ΦR(t-1) の部分に相当します。
2つ目は現在のノイズを表す式です。
ホワイトノイズに対して時点tによってブレる係数をかけています。
このブレる係数を条件付き標準偏差と呼びます。
3つ目は条件付き分散、2つ目の式の条件付き標準偏差の2乗を表す式です。
適当なパラメータω + 2つ目の式で表すことのできる前期のノイズの二乗に適当な係数a1をかけた式です。
適当なパラメータωと適当な係数a1と書きましたが注意点があります。
ここで表す条件付き分散とは2乗、つまり0またはほとんどの場合が正の数をとります。
そのためω、a1については「0以上である」という制約を設けます。
Rで実行
使うライブラリはfGarch
使う関数はgarchFitです。
install.packages("fGarch")
library(fGarch)
#使うデータは120日分の収益率データ
str(data.log.return$x9041)
num [1:120] -0.985 0 -0.331 -0.332 0.662 ..
# 一次の自己回帰モデルとその誤差モデルをつくる
# AR(1)+ARCHモデル
(arch.fit1<-garchFit(~arma(1,0)+garch(1,0),data=data.log.return$x9041,trace=F))
# estimate:係数の推定値
# Std.error:標準誤差
# t.value:t値
# Pr(>t):P値
# P値が小さければ帰無仮説「係数が0」は棄却され係数が意味を持つ
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(1, 0) + garch(1, 0), data = data.log.return$x9041,
trace = F)
Mean and Variance Equation:
data ~ arma(1, 0) + garch(1, 0)
<environment: 0x000001cd60b618b0>
[data = data.log.return$x9041]
Conditional Distribution:
norm
Coefficient(s):
mu ar1 omega alpha1
0.2365270 -0.0022778 1.1195896 0.3053496
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.236527 0.107295 2.204 0.0275 *
ar1 -0.002278 0.116571 -0.020 0.9844
omega 1.119590 0.206116 5.432 5.58e-08 ***
alpha1 0.305350 0.159451 1.915 0.0555 .
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Log Likelihood:
-194.0714 normalized: -1.617261
garchFit関数について
入力部分
garchFit(~arma(1,0)+garch(1,0),data=data.log.return$x9041,trace=F)
arma()の部分は前半部分でARモデルの次数、MAモデルの次数を指定します。
arma(1,0)で一次のARモデル
arma(3,0)で三次のARモデル
arma(0,1)で一次のMAモデル
arma(1,1)で一次のARMAモデルを指定します。
garch()の部分はARCHモデル、GARCHモデルの次数の指定をします。
garch(1,0)で一次のARCHモデル
garch(1,1)でその発展形である一次のGARCHモデルでの推定をします。
デフォルトではtrace = T であり詳細を見れますが結果だけを見たい場合が trace = F のほうが見やすいでしょう。
出力結果
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.236527 0.107295 2.204 0.0275 *
ar1 -0.002278 0.116571 -0.020 0.9844
omega 1.119590 0.206116 5.432 5.58e-08 ***
alpha1 0.305350 0.159451 1.915 0.0555 .
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
注目すべきは1列目のEstimate*4列目のPr(>|t|)です。
1列目のEstimateはモデルの係数の推定値を表します。
4列目のPr(>|t|)はP値を表します。
この値が大きければモデルへの当てはまりが悪いということです。
今回はar1についてのP値が0.9844と非常に大きい値をとっておりあてはまりが悪いですね。
余談
ちなみにこのデータについては0次のARIMAモデル、ARCHモデルの残差にskew-normal分布を指定するとあてはまりが良くなります。
(arch.fit3=garchFit(~arma(0,0)+garch(1,0),data=data.log.return$x9041,cond.dist="snorm",trace=F))
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.2447 0.1047 2.337 0.0194 *
omega 1.1286 0.2033 5.551 2.84e-08 ***
alpha1 0.2773 0.1454 1.907 0.0566 .
skew 1.2282 0.1442 8.519 < 2e-16 ***
---
Signif. codes:
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
やみくもにあてはまりの良いモデルを探すのではなく
・ARモデルの次数のあたりをつけるにはADF検定を使う
・残差を可視化しあてはまりの良い分布を考える
のが良いと考えています。
また、聞いたことがある方も多いと思いますがプロスペクト理論という心理効果が、このモデルを感覚的に理解できる一助になると思います。
まとめ
・ARCHモデルは分散不均一構造の代表的なモデル
・株価によくある「前回絶対値の大きなノイズが来たのであれば今回の分散は大きくなるだろう」のモデル
・Rで実行するにはfGarchライブラリのgarcFit関数を使う。
以上です、最後まで読んでいただきありがとうございました。
参考文献
現場ですぐ使える時系列データ分析 ~データサイエンティストのための基礎知識~ :横内 大介, 青木 義充 著(2014)
一橋大学の横内先生と株式会社QUICKという金融情報サービス会社の青木さんの本です。
私みたいな時系列データ初学者にとって最適な入口となってくれた本です。
時系列分析と状態空間モデルの基礎: RとStanで学ぶ理論と実装:馬場真哉 著(2018)
経済・ファイナンスデータの計量時系列分析:沖本竜義 著(2010)