About
Zeiler, M. D., Taylor, G. W., & Fergus, R. (2011, November).
Adaptive deconvolutional networks for mid and high level feature learning.
In Computer Vision (ICCV), 2011 IEEE International Conference on (pp. 2018-2025). IEEE.
Abstract
- 畳み込み層とmaxプーリング層を交互に重ねた、階層モデルを使って画像のdecompositionsを行う手法を提案
- a novel inference schema that ensures each layer reconstructs the input, rather than just the output of the layer directly beneath
- 層ごとに独立に学習をしていた従来手法でなく、層ごとにinputイメージを再構築して、学習する手法を提案
- 学習によって、各layerは画像の低レベルのエッジや、中レベルのエッジの交差や、高レベルの物体のパーツや、物体全体をそれぞれ認識するようになる
- Caltech-101, 256でのクラス分類でSIFT, その他の画像特徴量の手法よりも良い性能を出した
1. Introduction
- visionにまつわるタスクにおける重要な課題は「良い画像の特徴量を見つけること」
- SIFT, HOGはウルトラ有名な画像特徴量 (参考URL)
- ただしlow-levelな構造しか検出できなく、中・高レベルの特徴の把握が難しい
- 画像のlow-highまでの特徴量を教師なし学習で学習する手法を提案。
- 2つの問題を解決する。
- 回転やスケール等々の、入力画像に対する特徴量の不変性
- 層全体で学習していないこと
3. DBNや、Convolutional sparse codingでは層ごとに学習していた。
4. inputと層とのつながりは層が進むにつれ、薄れていく。
5. 多層化時の学習が不安定になる一因とのこと。
- 各画像ごとに計算される、switch varibalesを導入
- これにより、深い層もinput画像から直接学習ができるように
- ものすごくrobustになるとのこと
- ものすごい効率のよい学習手法になっているとのこと
- [WIP]従来手法(7 / 12 / 3,8,20 / 6,11 / 22, 16 <-> 4, 21 / 13, 15 )
- ボトムアップ
- 層ごとに独立に、教師あり学習を行っている(多分DBNとか、Autoencoderのことを言っている)
- pooling layersがない。
- スケールしない非効率な推定の仕組み
- 提案手法
- トップダウン(生成的(generative))
- 教師無し学習
- 全ての層がつながっている
- PSDもよく似た論文であるとのこと
- sparce codingのコンポーネントを追加した
- ただ、input画像を使うのでなく、一つ前の層を出力をcodingする点が異なる
- RBMを重ねあわせたDBNも同じ制限がある。
- factored representation that does not have directly perform explaining away
- 学習がとても遅い
2. Approach
- deconvolution + max-poolingの組み合わせ
- この章では、以下の4つが主な話題。
- 各層の構成: deconvolution, max-pooling/unpooling
- パラメータの推定
- パラメータ学習
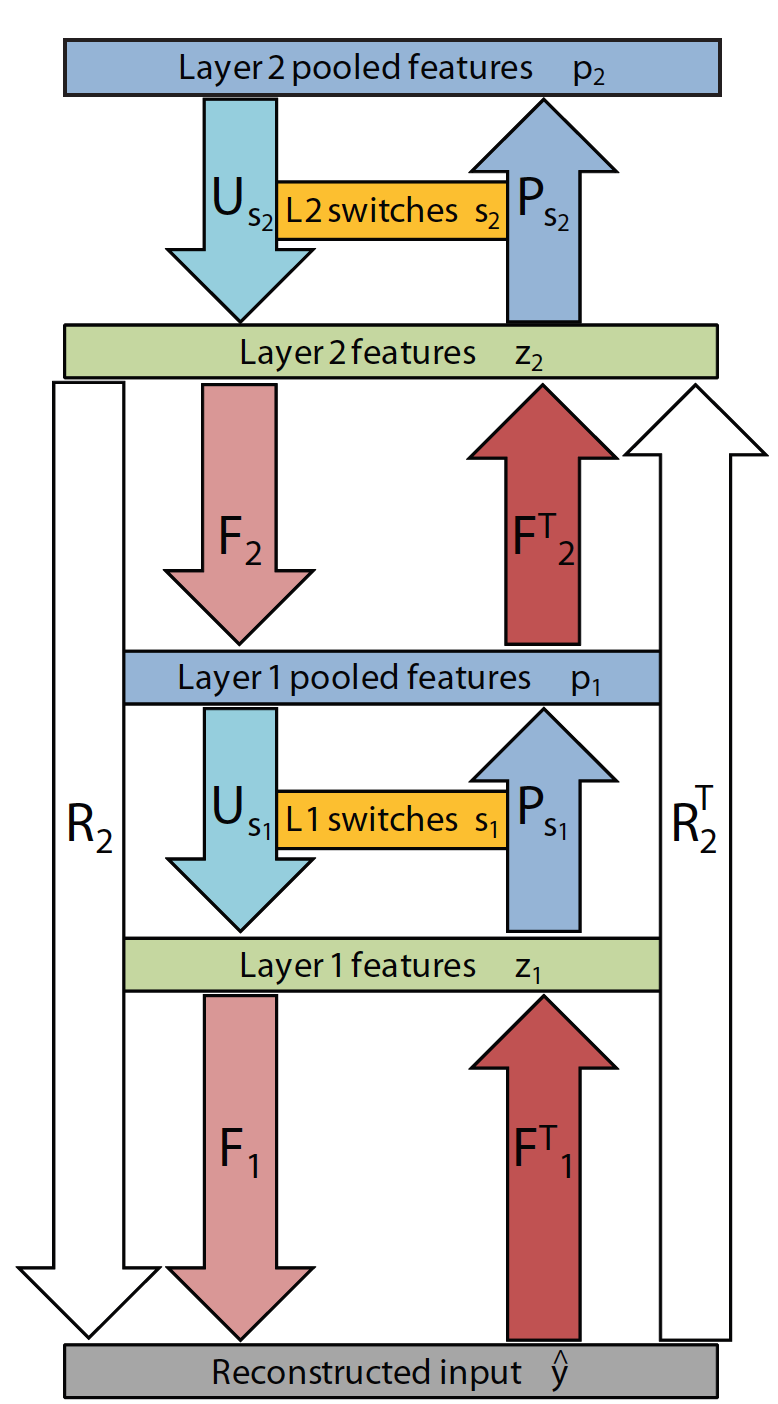
層の全体像の例
Deconvolution
- decovolutionはconvolutionの逆を行うもの。deconvolutionの式は、以下となる。
- $z_{k,l}$ : 第l層の、k番目のfeature map
- $\hat{y}_{l}$ : 第l層で再構築された入力画像
- $f^{c}_{k,l}$ : 第l層の、cチャンネル目の、k番目のフィルタの値
deconvolution
\begin{eqnarray}
\hat{y}^{c}_{l} &=& \sum^{K_l}_{k=1} z_{k,l} * f^{c}_{k,l}\\
&=& F_l z_l
\end{eqnarray}
- $F^{T}_{l}$ は deconvolutionの行列を転置したもので、普通の畳込み演算。
Pooling
- 普通のpoolingとの違いはswitchと呼ばれる, max値としてactivateした, feature mapの位置とその値を記録した変数をもつこと。
- feature map $z$ からpoolされた feture map $p$ を取り出す処理 $P_{s}$ と、逆にpoolされたfeature map $p$ から、feture map $\hat{z}$ に戻す処理 $U_{s}$, はそれぞれは以下のようになる。
Pooling
p = P_{s}z
Unpooling
z = U_{s}p
- 2つの処理は以下の関係を満たしている
Unpooling
U_{s} = P^{T}_{s}
Multiple layers
- 第l層での再構築の操作$R_l$は以下で表される。
\hat{y_l} = R_l z_l = F_1U_{s1}F_{2}U_{s2}...F_{l}z_{l}
- また、第l層での再構築の操作$R_l$の逆、すなわち入力画像からfeature mapを生成する操作を${R_l}^{T}$とすると、以下で表される
R^T_l = F^{T}_lP_{s_{l-1}}F^{T}_{l-1}P_{s_{l-2}}...P_{s_1}{F^{T}_{1}}
Learning
学習の概要
- 学習では畳み込み層のfilterの変数を学習したい
- ある層lの学習において、以下を行う。
- feature map $z$ と, filter $f$をガウス分布から初期化する。
- 以下をE epochs行う (提案手法では10回)
- [$z$の推定] 一つの入力画像毎に以下をT回行う (提案手法では15回)
- feature mapから、入力画像を再構築する
- 再構築した入力画像と、本来の入力画像の差分(reconstructionエラー $e$ )を計算する
- $e$を普通にネットワークにいれて伝搬
- 伝搬された値を使って、新しいfeature mapを計算する
- feature mapのsparsityを上げる
- 新しいfeature mapをpoolして、switchのlocation,valuesを更新する
- poolした値をunpoolしてzを更新する
- [$z$の推定] 一つの入力画像毎に以下をT回行う (提案手法では15回)
- [$f$の更新] 2.で推定されたzを使って、$f$ を更新する。
zの推定
3stepsで推定する。
1. Gradient step:
以下の計算で、新しい$z_l$を得る。
\begin{eqnarray}
g_l &=& R^{T}_{l}(R_{l}z_{l}-y)\\
z_l &=& z_l - \lambda_{l}\beta_{l}g_{l}
\end{eqnarray}
2. Shrinkage step:
- 微妙な値のzを0に置換するstep
z_l = max(|z_l| - \beta_{l}, 0)sign(z_l)
3. Pooling/unpooling:
- 更新された$z_l$をPoolingした後、すぐにUnpoolingする
- これによって、
- その層のfeature mapのPoolingまでを含めて学習される
- STEP 1、2によって、reviseされたfeature mapを使って、switch変数を更新できる
注意点
- 以下2点から非線形な処理であることに注意
- Shrinkage stepそのものが非線形な処理であること
- switchの更新によって$R_{l}$が変わりえること
fの更新
各変数を以下の通りとして、目的の損失関数を定義する
- $z_{k,l}$ : 第l層の、k番目のfeature map
- $y$ : 入力画像
- $\hat{y}_{l}$ : 第l層で再構築された入力画像
lossfunction
C_{l}(y) = \frac{\lambda_{l}}{2}||\hat{y}_{l} - y||^{2}_{2} + \sum^{K_l}_{k=1}|z_{k,l}|_{1}
- 損失関数を $f$ で微分した値を0とすることで得られる、以下の式を解くことで更新した $f$ を得る。
\sum^{N}_{i=1}({z^{i}_{l}}^{T}P^{i}_{s_{l-1}}{R^{i}_{l-1}}^T)\hat{y_l}^{i} = \sum^{N}_{i=1}({z^{i}_{l}}^{T}P^{i}_{s_{l-1}}{R^{i}_{l-1}}^T)y^{i}
3. Application
- 詳しくは割愛
- 提案した手法をつかって、クラス分類を行う方法を提案している。
- 提案手法はあくまで教師なし学習なので、一番最終層の上にSVMを乗っけて、クラス分類器を作成する、というもの
4. Experiment
- 可視化したったでという内容と、Applicationの内容なので、詳細は割愛。
所感
他の最近の手法に比べて、学習の速さ、精度はどうなっているのか、最近の手法ではみかけないけど、何か問題点があるのか?