目標
以下、2つのドキュメントに書いてある内容を理解する。
バイアスメトリクス
Amazon SageMaker Clarifyの元ネタ論文であるところの Fairness Measures for Machine Learning in Finance の後ろの方に各バイアスメトリクスの定義と簡単な説明をまとめたテーブルが記載されている。
クラクラする。何度読んでもクラクラする。今日からはもうクラクラしないことを目指す。
記号の定義
例として、ローンの審査が通すか ($y=1$) 通さないか ($y=0$) を判断する機械学習モデルを考えましょう。
特徴量としては例えば申込者の収入、総資産、借金の履歴、ローン金額といったものを用いるでしょう。さらには、年齢や性別、職業、国籍、人種など、なんだかやばそうな特徴量を使うかもしれません。こういった特徴量のことを論文内では restricted feature だとか、protected characteristic だとか demographic group だとか呼んでいます。あと一般化のためか、ファセット (facet) と呼んだりもしています。(ファセットは「一面」とか「側面」とかそういう意味ですが、バイアス分析の「切り口」みたいな訳が沿うかもしれません。)
トレーニングに用いるデータセットがバイアスを含んでいて、例えば国籍が日本人だったらローンに通りやすく、その他の場合ローンに通りにくいといったケースがあるかもしれません。(ありそうですね。)このとき、日本人のグループのことを advantaged group ($a$)、その他のグループのことを disadvantaged group ($d$) などと呼んでいます。
$n$ 個サンプルがあるデータセットの中にいるローンの審査が通った人の数を $n^{(1)}$、通らなかった人の数を $n^{(0)}$ と書くことにします。それぞれのうち日本人の数を $n_a^{(1)}$、$n_a^{(0)}$、その他の数を $n_d^{(1)}$、$n_d^{(0)}$ のように書きます。(国籍に対して分析を行いたい場合の例です。性別に対して分析したい場合は、例えば男性が advantaged group になったり、女性が disadvantaged group になったりするでしょう。あくまで例ですよ。)
当たり前ですが、データセット内の日本人の数は $n_a:=n_a^{(0)}+n_a^{(1)}$、その他の数は $n_d:=n_d^{(0)}+n_d^{(1)}$ のようになります。
ここまでトレーニングデータ内の実測値を定義しましたが、予測値に関してはハットをつけて $\hat{y}$ とか $\hat{n}$ とか書きます。
これで準備完了です。
トレーニング前バイアスメトリクス
モデルのトレーニングを行う前にすでにデータに存在するバイアスを検出するためのバイアスメトリクス集です。
Class imbalance (CI)
これは単純ですね。分析対象の特徴量のアンバランス加減を表すメトリクスで、以下のように定義されます。
$$CI=\frac{n_a-n_d}{n_a+n_d}=\frac{n_a-n_d}{n}$$
例えばデータセットに日本人が90人、その他が10人含まれていた場合、
$$CI=\frac{90-10}{90+10}=0.8$$
となります。CIの定義域は $-1\le CI\le 1$ であり、(分析対象の特徴量が二種類の場合は)0に近いほどバランスが取れていることになります。0.8はアンバランスですね。
「日本人以外のデータが少ないことに起因する国籍に関するバイアスがありそうですか?」といった質問に答えるために使用できます。
Difference in positive Proportions of Labels (DPL)
「正例ラベル比率の差」などと訳しましょう。先ほどの例のように、日本人はローンが通りやすく、その他の国籍の方々がローンに通りにくい、といった傾向があった場合に DPL が大きくなります。定義は以下の通りです。
$$DPL=\frac{n_a^{(1)}}{n_a}-\frac{n_d^{(1)}}{n_d}:=q_a-q_d$$
例えば、日本人の8割がローン審査に通り、その他の国籍の方々は3割しか通らないすると、
$$DPL=0.8-0.3=0.5$$
となります。CIと同じく定義域は $-1\le DPL \le 1$ であり、$DPL=0$ となるとき 「demographic parity が達成されている」と表現するみたいです。
「それぞれの国籍間でラベルの割合が異なることに起因して、ML予測がバイアスを持つかも?」という心配に答えてくれます。
Kullback-Leibler Divergence (KL)
お馴染み (?) カルバックライブラーダイバージェンスです。2つの確率分布間の距離のようなものを表現するのに使われます。ここでは、グループ $a$ のラベル分布を $P_a(y)$、グループ $d$ のラベル分布を $P_d(y)$ とします。KLダイバージェンスの定義は以下の通りです。
$$KL(P_a,,P_d)=\sum_y P_a(y)\log\left[\frac{P_a(y)}{P_d(y)}\right]\ge 0$$
(分数と対数がセットで出てくると、それはもう情報量の差を取っているようなものです。確率分布がかかって和を取っているので期待値の差ですが。そういう量を分布間の距離とみなしているんですねえ。)
ラベル分布と言っても今はローンの審査が通るか通らないかの二値しか考えていないため、単純です。例えば先ほどのように、日本人の8割がローン審査に通り、その他の国籍の方々は3割しか通らないすると、
$$KL = 0.8\cdot\ln(0.8/0.3)+0.2\cdot\ln(0.2/0.7)=0.53$$
となります。足し算のひとつ目の項が $y=1$(ローン審査通過)のケースで、ふたつ目の項が $y=0$(ローン審査落ち)のケースの計算になっています。定義域は $[0,,+\infty)$ であり、「距離」らしく、同じ分布であれば0を取ります。
「日本人とそれ以外でローンの審査結果の分布がどれくらい異なりますか?」といった質問に答えてくれます。
Jensen-Shannon Divergence (JS)
ジェンスン・シャノンじゃなくてイェンセン・シャノンと読むそうです。
KLダイバージェンスは定義から $KL(P_a,,P_d) \neq KL(P_d,,P_a)$ であり、非対称性があります。それを次のように無理やり (?) 対称的にしたのがJSダイバージェンスです。
$$JS=\frac{1}{2}[KL(P_a||P)+KL(P_d||P)]$$
ただし、$P=(P_a+P_d)/2$ です。定義域は $[0,,\ln(2))$ ですが、同じ分布であれば0となるのはKLと同様です。
KLと同じく「日本人とそれ以外でローンの審査結果の分布がどれくらい異なりますか?」といった質問に答えてくれます。
Lp-norm (LP)
KLダイバージェンスやJSダイバージェンスは情報理論の観点で定義づけられた確率分布間の距離の指標ですが、もう少し単純に距離っぽい計算をするのがLp-normです。定義は以下のようになり、$p=2$ のときは三平方の定理的な、いわゆる距離(ユークリッド距離)を計算する式になっていることがわかると思います。
$$L_p(P_a,,P_d)=\left(\sum_y||P_a-P_d||^p\right)^{1/p}$$
一応参考までに、点 $(x_1,,y_1)$ と点 $(x_2,,y_2)$ の距離 $L$ は次のようになります。
$$L=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
一緒の形ですね。SageMaker Clarifyでは $p=2$ としてメトリクスを計算してくれるようです。例えば、同じく日本人の8割がローン審査に通り、その他の国籍の方々は3割しか通らないすると、
$$L_2=\sqrt{(0.8-0.3)^2+(0.2-0.7)^2}\sim0.7$$
となります。
KLやJSと同じく「日本人とそれ以外でローンの審査結果の分布がどれくらい異なりますか?」といった質問に答えてくれます。
Total Variation Distance (TVD)
「全変動距離」などと訳されます。L1ノルム(差の絶対値の和)の半分です。
$$TVD=\frac{1}{2}L_1(P_a,,P_d)$$
以下の図でいうと黄色の部分と緑の部分を足して2で割ったものです。

図出典: https://www.bananarian.net/entry/2018/08/29/160140
え、なんで2で割るんだって?そりゃあ、ふたつの確率分布が完全に分離してるとき、TVDが1になると嬉しいじゃないですか。
KLやJSやLp-normと同じく「日本人とそれ以外でローンの審査結果の分布がどれくらい異なりますか?」といった質問に答えてくれます。
Kolmogorov-Smirnov (KS)
コルモゴロフ・スミルノフと読みます。ある特徴量(ファセット)に対して最も不均衡なラベルを見つけます。
$$KS=\max(|P_a(y)-P_d(y)|)$$
例えば、大学の受験者のうち男性 ($a$) の合格、補欠、不合格の割合が20%、40%、40%で、女性 ($d$) のそれぞれの割合が70%、10%、20%だった場合、
$$KS=\max(|0.2-0.7|,,|0.4-0.1|,,|0.4-0.2|)=0.5$$
となります。性別に対するラベル分布の最大の乖離が0.5であり、合格率で一番大きな違いがあることを示しています。
「性別による受験結果の格差はどれくらい?」という質問に答えてくれます。
Conditional Demographic Disparity (CDD)
おそらくこのメトリクスがClarifyの肝。Amazon ScienceのSageMaker Clarifyについて書かれたブログでもCDDがフィーチャーされています。Conditional Demographic Disparity in Labels の略で CDDL と表記されることもあります。
2020年のこちらの論文で発明されたメトリクスとのことです。
このメトリクスを理解するにはいくつかのステップが必要です。
- シンプソンのパラドックス (Simpson's Paradox) を知る
- Demographic Disparity を理解する
- Conditional Demographic Disparity を理解する
1. シンプソンのパラドックス
ITmediaの記事がとてもわかりやすいのでそれを見ればOKです。
特に次の図にもうすべてが集約されています。

図出典: シンプソンのパラドックス(Simpson's paradox)とは? ITmedia
架空の西高校と日比谷高校があったとき(西高校なんて、いかにも架空の高校らしい名前ですね)、とある模擬試験の西高校の男子生徒の平均点は90点、女子生徒の平均点は70点、日比谷高校の男子生徒の平均点は85点、女子生徒の平均点は60点だったとき、どう考えても西高校の勝利に見えますよね。しかし、男子女子合わせた平均点を計算すると日比谷高校の勝利となっていました。これは陰謀だ!となるわけなのですけれども、こんな感じでグループ間で見られた相関関係が、集約した全体では成り立たないことがある、というのがシンプソンのパラドックスです。
どういうときにこんなパラドックスが起こるかというと、それぞれのグループの構成(男女比)に偏りがあるときです。
ITmediaの記事とまったく同じ解説をしますが、例えば、それぞれ架空の西高校と日比谷高校の人数構成が以下のようになっていたとします。
| 男子 | 女子 | 全体 | |
|---|---|---|---|
| 架空の西高校 | 45人 | 55人 | 100人 |
| 架空の日比谷高校 | 80人 | 20人 | 100人 |
架空の西高校はやや女子生徒が多く、日比谷高校は男子が多くなっています。ここで、それぞれの高校の全員分の合計点と全体の平均点を計算してみましょう。
| 男子の合計点 | 女子の合計点 | 全体の平均点 | |
|---|---|---|---|
| 架空の西高校 | 4050点(=90点×45人) | 3850点(=70点×55人) | 79点(=7900点/100人) |
| 架空の日比谷高校 | 6800点(=85点×80人) | 1200点(=60点×20人) | 80点(=8000点/100人) |
日比谷高校の人数の多い男子生徒が得点を稼いでくれたことで、全体の平均としては日比谷高校がやや勝る結果となりました。こうして西高校の生徒たちも悔しい気持ちを感じつつ、男子同士、女子同士だと勝ってるしいいかなと思ったりもします。統計を扱うとき、ある一側面だけ見て結論を出してはいけないのですね。
2. Demographic Disparity
模擬試験の例ではバイアス感はそんなにありませんが、これが男女間の大学院の合格率のデータだったらどうでしょう。1973年、カリフォルニア大学バークレー校では男女で大学院の合格率に差異が見られたようです。(以下のデータは「jamoviで学ぶ心理統計」のページから引用しています。)
| 志願者数 | 合格率 | |
|---|---|---|
| 男性 | 8442 | 44% |
| 女性 | 4321 | 35% |
なんと、女性の方が合格率が9%も少ないという結果になってしまっています。しかし、シンプソンのパラドックスをご存知の皆さんはこう思うでしょう。「ほーん、で、内訳は?」
では、学科ごとの男女それぞれの志願者数と合格率を見てみましょう。
| 学科 | 男性の志願者数 | 合格率 | 女性の志願者数 | 合格率 |
|---|---|---|---|---|
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 272 | 6% | 341 | 7% |
なんと、全体では女性の合格率は少なかったものの、6つの学科のうち4つで女性の合格率の方が高いということがわかりました。にも関わらず、なぜ全体として女性の合格率が低いのでしょう。それは、それぞれの学科の志願者数と合格率を見るとわかります。女性の志願者数を見ると学科C/D/E/Fに偏っています。しかし、これらの学科の合格率は男女ともに30%前後、学科Fに至っては6-7%しかありません。
つまり、このデータでわかることは、この年、この大学院では、女性は「難しい」学科に志願する傾向にあったということです。全体としては合格率に偏りがあるように見えますが、学科単位で見るとそこまで顕著な違いは見られず、何か差別的な要素は働いていなさそうに思えます。
ここで、2つの記号を定義します。(「の」のフォントが素敵どすなあ。)
$$D=\frac{\text{女性の不合格者の数}}{\text{全不合格者の数}}=\frac{n_d^{(0)}}{n^{(0)}}$$
$$A=\frac{\text{女性の合格者の数}}{\text{全合格者の数}}=\frac{n_d^{(1)}}{n^{(1)}}$$
先ほどのデータで計算すると、大体、
$$D=\frac{4321\times 0.65}{8442\times 0.56+4321\times 0.65}\sim 0.37$$
$$A=\frac{4321\times 0.35}{8442\times 0.44+4321\times 0.35}\sim 0.29$$
となります。この $D$ と $A$ の差を取ったのが Demographic Disparity (DD) です。
$$DD_d=D-A=\frac{n_d^{(0)}}{n^{(0)}}-\frac{n_d^{(1)}}{n^{(1)}}$$
DDは「森を見て木を見ず」的な指標であるため、「内訳は?」というのが気になってきます。そこで、DDをグループごと(学科ごと)に計算して、カウント数で重み付け平均を取ったものが Conditional Demographic Disparity (CDD) です。
$$CDD=\frac{1}{n}\sum_i n_i\cdot DD_i$$
先ほどの例でいうと $i$ は学科A〜Fのいずれか、$n_i$ はそれぞれの学科の女性の志願者数、$n$ は女性の全志願者数となるわけですね。
SageMaker Clarifyによるトレーニング前バイアスメトリクス測定の方法
SageMaker Clarifyでトレーニング前のデータのバイアス分析を行う手順は以下のようになります。
-
DataConfigを準備 -
BiasConfigを準備 - SageMaker ClarifyのジョブとしてSageMaker Processing Jobを準備
- Processing Jobを実行
(1) の DataConfig では分析対象のテーブルデータの情報を教えてあげます。以下のように、Amazon S3上に置いたトレーニングデータのパスや、バイアス分析結果のレポートの保存場所を与えたり、予測対象のラベルはどれで、テーブルデータにはどんなカラムがあるのか、データセットのフォーマットは何なのかということを定義します。
from sagemaker import clarify
bias_s3_prefix = "bias/generated_bias_report"
bias_report_output_path = "s3://{}/{}/data".format(bucket, bias_s3_prefix)
data_config = clarify.DataConfig(
s3_data_input_path=data_s3_uri,
s3_output_path=bias_report_output_path,
label="star_rating",
headers=df.columns.to_list(),
dataset_type="text/csv",
)
(2) の BiasConfig では、どの「切り口」でバイアス分析を行うかを定義します。先ほどの例でいうと facet_name に「性別」のカラムを指定したりします。そして、ラベルの予測値がいくつ(以上)であったらポジティブなラベルであるのかということを label_values_or_threshold で定義します。ローンの例でいうと、予測値が0から1の範囲で確率として出力されるとすると、例えば0.5以上であればローン審査に通る、0.5未満であればローン審査に通らないというように閾値を設定します。(以下のコードではカスタマーレビューの星評価 star_rating が5か4であればポジティブ、3か2か1であればネガティブと設定しています。)
bias_config = clarify.BiasConfig(
label_values_or_threshold=[5, 4],
facet_name="product_category"
)
そして、バイアス分析を行うためのSageMaker Processing Jobの準備をします。
processor = clarify.SageMakerClarifyProcessor(
role=role,
instance_count=1,
instance_type="ml.m5.xlarge",
sagemaker_session=sess
)
ここで定義した processor の run_pre_training_bias メソッドに DataConfig と BiasConfig を渡して実行すると Apache Spark で分散ジョブが流れます。
processor.run_pre_training_bias(
data_config=data_config,
data_bias_config=bias_config,
methods=["CI", "DPL", "CDDL"],
wait=False,
logs=False
)
このとき、methods 引数で計算したいメトリクスを指定することができます。何も指定しないとSageMaker Clarifyが計算できるすべてのメトリクスが求められます。
以下のSageMaker Clarifyの論文でもメトリクスの簡単な解説が書かれているのですが、トレーニング前のバイアスメトリクスに関しては、CI (Class Imbalance)、DPL (Difference in positive proportions in observed labels)、CDDL (Conditional Demographic Disparity in Labels) のみ記載があります。(実際のところ定かではないですが)あんまりたくさんのメトリクスを眺めても解釈が難しいので、基本的にCI、DPL、CDDLだけ見とけばいいんじゃないかなあと思ってます。詳しい人いらっしゃったらコメントいただけると助かります。
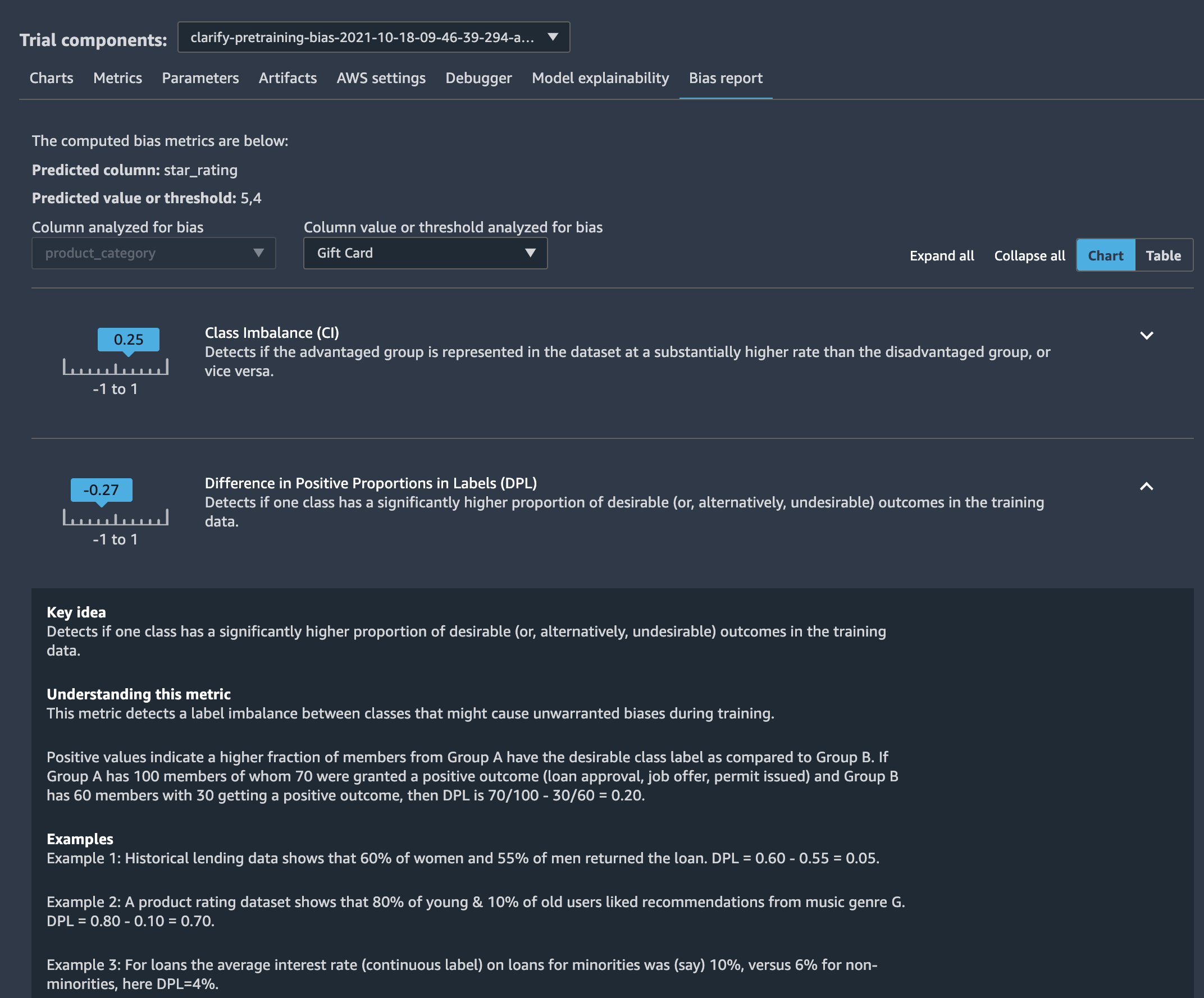
ちなみに出力されるバイアスレポートは以下のようなものです。
SageMaker Studioで見ると、それぞれのメトリクスの説明含めてもう少し詳しく見れます。
トレーニング後バイアスメトリクス
トレーニング後に機械学習モデルの推論にバイアスがかかってしまっていないかを分析するのに用いるメトリクス集です。
Difference in positive Proportions in Predicted Labels (DPPL)
トレーニング前メトリクスである DPL (Difference in positive Proportions in Labels) はファセット(性別など)ごとのラベル比率の差を見るメトリクスでしたが、DPPLではラベルではなくてモデルの予測結果の比率の差を見ます。
$$DPPL=\frac{\hat{n}_a^{(1)}}{n_a}-\frac{\hat{n}_d^{(1)}}{n_d}:=\hat{q}_a-\hat{q}_d$$
例えばモデルが、日本人のローン申込者の7割が審査を通過し、その他の国籍の方々の4割が通過すると予測したとすると、
$$DPPL=0.7-0.4=0.3$$
となります。DPLとDPPLを比較すると、もともとトレーニングデータにあったバイアスが、モデルのトレーニング後にどれだけ増加したのか減少したのかをチェックすることができます。
Disparate Impact (DI)
DPPLではポジティブな予測ラベル比率の「差」を計算しましたが、比較を行いたい時には「差」じゃなくて「比率」で見てもいいですよね。というわけで割り算をしたものを Disparate Impact (DI) と呼びます。
$$DI=\frac{\hat{q}_d}{\hat{q}_a}$$
先ほどの例でいうと、機械学習モデルにより、日本人のローン申込者の7割が審査を通過し、その他の国籍の方々の4割が通過すると予測されたとすると、
$$DI=\frac{0.4}{0.8}=0.5$$
となります。$DI=1$ の場合、バランスが取れていること(demographic parity)を表します。
Fairness Measures for Machine Learning in Finance によるとアメリカの雇用に関する規制当局は、格差の影響を測定するための「rule of thumb(経験則)」として80%を目安にしているようです。DIが0.8を下回ると差別待遇があるとみなされるのでしょう。
Difference in Conditional Acceptance (DCAcc)
DCAccでは、実際のポジティブラベルと予測のポジティブラベルの割合を比較し、ファセット(性別など)の間で割合が同じであるかどうかを評価します。
$$DCAcc=\frac{n_a^{(1)}}{\hat{n}_a^{(1)}}-\frac{n_d^{(1)}}{\hat{n}_d^{(1)}}:=c_a-c_d$$
例えば、データセット内に日本人(ファセット $a$)のデータが100個、それ以外の国籍の方(ファセット $d$)のデータが50個あったとしましょう。実際そのうち、それぞれ70人と20人がローン審査を通過しました。しかし、このデータで学習したモデルはそれぞれ60人と30人がローン審査を通過するんじゃないかなと予測しました。つまり、実際よりもモデルの方が日本人に対して有利に、その他の方々に対して不利に予測していまっています。このとき、
$$DCAcc=\frac{70}{60}-\frac{20}{30}=\frac{1}{2}$$
となります。逆に、例えば、実際は日本人50人がローン審査を通過し、その他の国籍の方々40人がローン審査を通過したとしましょう。(実際のラベルの差よりもモデルの予測の方がバイアスが小さくなったケースです。)このとき、
$$DCAcc=\frac{50}{60}-\frac{40}{30}=-\frac{1}{2}$$
となります。このように、DCAccが正の値を持つと「モデルはバイアスを持っている」、負の値を持つと「モデルは多様性を持っている」、もしくはイマドキの言葉で言うと「affirmative action」を実践している、と言えるかもしれません。
また、面白いことに、今回のケースでDPPLを計算すると、
$$DPPL=\frac{60}{100}-\frac{30}{50}=0$$
となり、DPPLの観点からするとバイアスは存在しないことになってしまいます。ひとつのメトリクスだけ追っていてもバイアスがあるかどうかは判断しきれないというのが分かりますね。
Difference in Conditional Rejection (DCR)
DCAccでは、例えばローンを通過したケースのような、acceptされた場合に対して計算していましたが、DCRでは逆にrejectされた場合に対して計算を行います。DCAccとあまり変わらないので、定義だけ書いて解説は省略します。
$$DCR =\frac{n_d^{(0)}}{\hat{n}_d^{(0)}}-\frac{n_a^{(0)}}{\hat{n}_a^{(0)}}:=r_d-r_a$$
詳しくは SageMaker のドキュメント等を参照してください。
Recall Difference (RD)
まあ、ファセット間でのリコールの差です。TP (True Positive)、FN (False Negative)、TPR (True Positive Rate) と置くと、以下のように定義されます。
$$RD=\frac{TP_a}{TP_a+FN_a}-\frac{TP_d}{TP_d+FN_d}=TPR_a-TPR_d$$
実際にローンを通過した人 (TP+FN) のうち、通過すると予測された人 (TP) がどれだけいるか、といういわゆるリコール(再現率)を異なるファセット(日本人とその他)で比較するメトリクスです。
Difference in Acceptance Rates (DAR)
適合率の差です。FP は False Positiveの略です。
$$DAR=\frac{TP_a}{TP_a+FP_a}-\frac{TP_d}{TP_d+FP_d}$$
ローンを通過すると予測された人 (TP+FP) のうち、本当にローンを通過した人 (TP) の割合という、いわゆる precision(適合率)を異なるファセットで比較するメトリクスです。
Difference in Rejection Rates (DRR)
DARの逆で、TN を True Negative として、以下のように定義します。
$$DAR=\frac{TN_d}{TN_d+FN_d}-\frac{TN_a}{TN_a+FN_a}$$
ローンに落ちると予測された人 (TN+FN) のうち、実際にローンの審査に落ちてしまった人 (TN) の割合を異なるファセット間で比較するメトリクスです。
例えば、モデルが日本人のローン申請のうち100件を拒否したものの、実際は要件を満たしていなかったのは80人だったとします。また、モデルがその他の国籍の方々のローン申請のうち50件を拒否したものの、実際に要件を満たしていなかったのは40人だったとします。このとき、
$$DAR=\frac{40}{50}-\frac{80}{100}=0$$
となり、バイアスがないことを表します。
Accuracy Difference (AD)
Accuracyの差です。
Treatment Equality (TE)
有利なファセットと不利なファセットの間の偽陽性と偽陰性の比率の差を測定します。
$$TE=\frac{FP_a}{FN_a}-\frac{FP_d}{FN_d}$$
例えば、日本人のローン申請が100件、その他の国籍の方々のローン申請が50件あったとしましょう。そのとき、日本人の申請8件が機械学習モデルによって誤って拒否 ($FN_a$) されてしまい、逆に、6件は誤って承認 ($FP_a$) されてしまったとします。また、その他の国籍の方々も5件が誤って拒否 ($FN_d$) されてしまい、2件は誤って承認 ($FP_d$) されてしまったとします。このとき、
$$TE=\frac{6}{8}-\frac{2}{5}=0.75-0.40=0.35$$
となります。実はこの場合、日本人 ($a$) とその他の国籍の方々 ($d$) それぞれのaccuracyを計算すると、
$$ACC_a=\frac{100-8-6}{100}=0.86$$
$$ACC_d=\frac{50-5-2}{50}=0.86$$
となり、Accuracy Difference (AD) は0なのです。つまり、ADでは見つからなかったバイアスがTEで検出できたことになります。
Conditional Demographic Disparity in Predicted Labels (CDDPL)
CDD (=CDDL) を実際のラベルでなく予測ラベルに対して計算したものです。
$$DPPL_d=\frac{\hat{n}_d^{(0)}}{\hat{n}^{(0)}}-\frac{\hat{n}_d^{(1)}}{\hat{n}^{(1)}}$$
大学全体だと見られたバイアスが学科ごとだと見られなくなるかもしれません。そういうことをチェックできるメトリクスです。
Counterfactual Fliptest (FT)
最後に説明が大変なメトリクスが来てしまいました。
Couterfactualは「反事実」とか「反事実現実」とか訳される、因果推論などの分野で出てくる言葉です。
お酒を飲む人が心筋梗塞になったとき、それが本当にお酒の影響なのか確認するためには、その人が「もしもお酒を飲まなかったら?」という「反事実」を分析しなくてはいけません。
しかし、現実にはそんなことはできないので、お酒を飲む集団とお酒を飲まない集団を比較します。ただし、シンプルに集団を比較するのではなく、お酒を飲む人達と飲まない人達で特に特徴が似通っているグループで比較を行います。
こうした比較の仕方を「フリップテスト」と呼びます。お酒を飲むか否かの「ビット」だけを反転(フリップ)して比較を行うイメージです。
では、どのように似通ったグループを抽出するかというと、ここでは簡単に、k最近傍法 (k-NN) を使います。ローン審査の例に戻ると、例えば、日本人以外の国籍の方のデータの最近傍にあるk人の日本人データを取ってきます。そのk人で多数決をとって、ローン審査を通過する人の方が多そうか否かを評価します。これを日本人以外の国籍の方 $n_d$ 人に対して繰り返します。
ローンに落ちると予測された (unfavorable outcome) 日本人以外の国籍の方のうち、最近傍の日本人の多くがローンを通過する (favorable outcome) と予測された人の数を $F^+$ とし、ローンに通過すると予測された (favorable outcome) 日本人以外の国籍の方のうち、最近傍の日本人の多くがローンに落ちる (unfavorable outcome) と予測された人の数を $F^-$ とすると、FTは以下のように定義されます。
$$FT=\frac{F^+-F^-}{n_d}$$
国籍という要素をフリップしたときに、良い結果になるケースが多いのか($FT>0$)、悪い結果になるケースが多いのか($FT<0$)、もしくはバランスが取れているのか($FT=0$)を判定するメトリクスです。まとめると、ファセット $d$ の各サンプルと類似したファセット $a$ のサンプルを調べ、異なるモデル予測を持っているかどうかを評価する、というのがFTでやっていることです。
最後に
いかがでしたでしょうか。SageMaker Clarifyで分析できるメトリクスは非常に多岐に渡りますが、じっくり見ていくとひとつひとつはそう難しい概念でもありません。
SageMaker Clarifyを試すには、SageMaker Immersion Day のハンズオンコンテンツや、 実践 AWSデータサイエンス に関連する ワークショップ など、さまざまなパスが用意されています。ぜひお試しいただき、手元のデータのバイアス分析を行なってみてはいかがでしょうか。