この記事はMDC Advent Calendar 2020 17日目の記事です。
1217は素数ですが、20201217は素数ではありません( $20201217 = 3 \times 73 \times 92243$ )。
今回は技術を用いた結果とかに示すグラフについて説明いたします。
なぜこんな記事を書いたのか
誤解を招くグラフ、というものがあります。
グラフは基本的にデータを可視化した上で傾向や状態を示す有効な手段でありますが、時に相手に誤解を与える表現も可能です。悪く言えば騙すということですね。
下記に述べるグラフというものは今に始まったことではないですが、あちこちで見かけるのでせめてこれを読んだ方にはしてほしくないな、という思いから書きました。
ちなみに、データサイエンティスト協会が作成しているスキルマップによりますと、不適切なグラフを作るのはDS(Data Scientist)以前の方だそうです1。
なお、以下の例で出てくるデータについては筆者が適当に作ったデータセットであり、なにか本物のデータを模したものではございません。
その1:定番中の定番、3Dグラフ
みんな大好きExcelの謎機能。
3D棒グラフ、3D円グラフが代表的ですね。
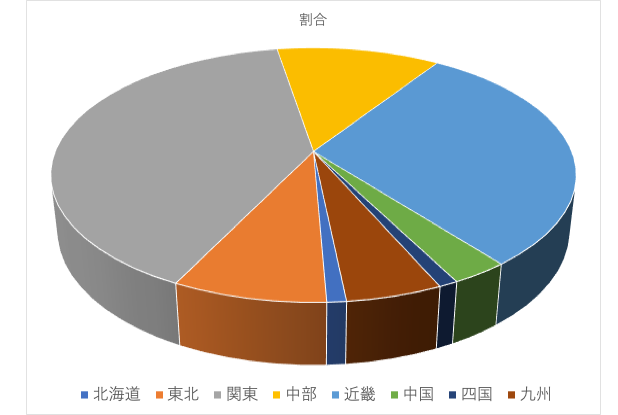
例えば、以下のデータを3D円グラフで表すとこうなります。
| 出身地域 | 割合(%) |
|---|---|
| 北海道 | 1.0% |
| 東北 | 8.0% |
| 関東 | 40.0% |
| 中部 | 12.0% |
| 近畿 | 30.0% |
| 中国 | 3.0% |
| 四国 | 1.0% |
| 九州 | 5.0% |
手前にある、東北と四国と九州(合わせて12%)がなんか30%くらいはありそうに見えるし、40%と凡そ半分近くを占めている関東が全然そんな気がしないしとにかく誤解を与えますね。原因はかの有名な遠近法です。人間の視覚的性質によって正確な情報を与えられないから不適という言葉に尽きます。
ところで、私は関西出身なので塾や予備校と言っても精々駿台、河合、鉄緑会くらいしか知らないのですが、関東だと塾が乱立してるためか広告が積極的に行われてます。電車に乗っていると、2020年度合格者数xxx人に増加!というデータとそれを示す3D棒グラフもあります。
よく数字を見るとちょっと人数が増えただけだったりしますし、そもそも1学年における在籍者数も違うはずなので微妙な気分になったりします。
その2:秘技、2軸グラフ
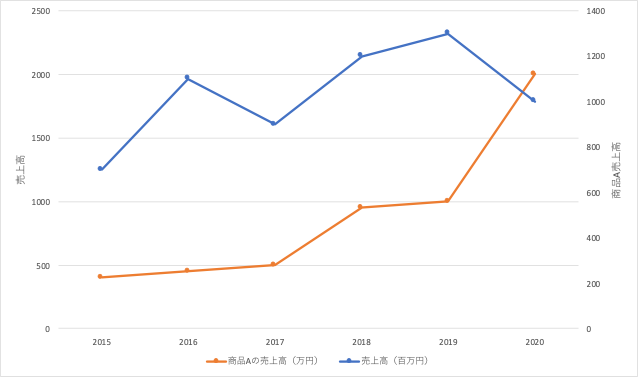
いわゆる縦軸が左右両方にあるやつ。
必ずしも2軸グラフが悪いとは言い切れないですが、得てして数字の大小が異なる(尺度が異なる)ことが多いので誤解を与える恐れがあります。
この例ですとある会社の売上高(百万円)とその会社の商品Aの売上高(万円)の推移を表したグラフになります。
たしかに、商品Aの売上高は伸びていってるのは事実ですが、それが全体の売上高に影響を与えるほどの割合・要素かというと必ずしもそうではありません。
どちらかといえば、他の商品のデータも含めた上で積み上げ棒グラフとかで示して上げるほうが良いと思います(そうすると落ち込んだ原因の商品や部門が明確になるため)。
その3:飛び道具、大きさ違い
グラフの要素、そもそものグラフの大きさを変えているパターン。
「いや、それ数字で表現したら大したことないじゃん・・・」と気づかれるのがオチなのでやめましょう。
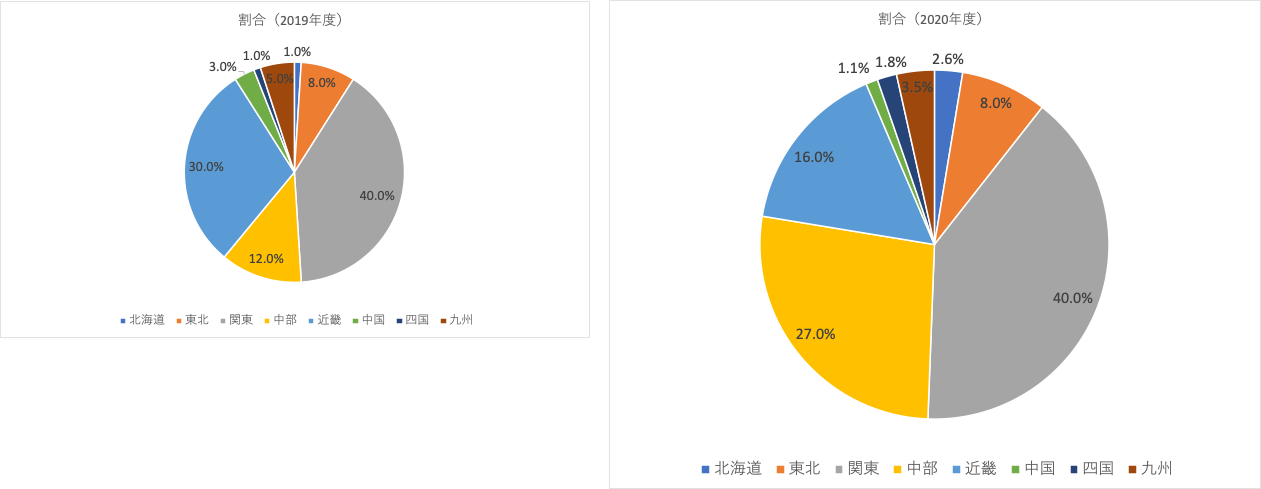
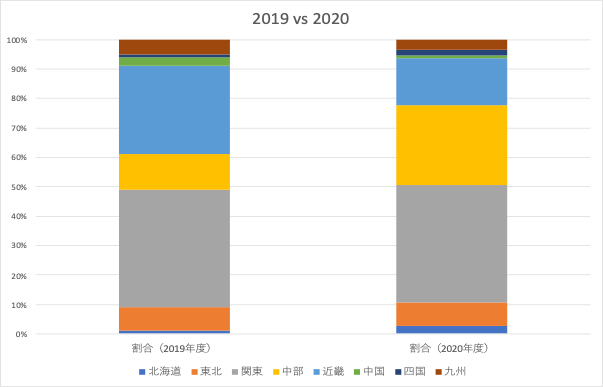
またしても例はとあるコミュニティのメンバにおける出身地の割合(2019年度と2020年度)。
この例は円グラフの大きさを変えて中部地方出身者の増加を強調したい意図があるのでしょう。
しかしながら、比較対象を正確に読み解けないこと、そして過度に効果を強調する以外他ならないので不適切です(この例での解釈だと中部地方が増えたのは事実ですが、一方で関西が大幅に減ったことが原因とも考えられるので、コミュニティから抜けた人が関西人だったりしないか等の検討も必要だと思われます)。
その4:伝家の宝刀、軸の値替え
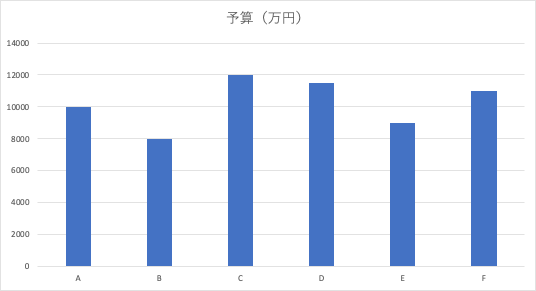
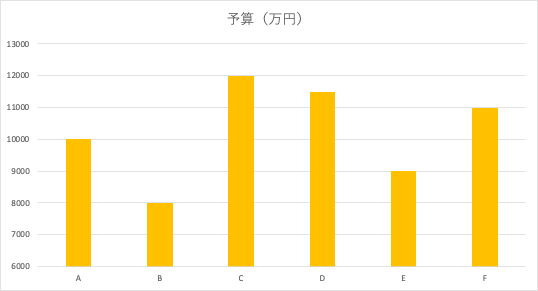
下記のようななんかよくわかんないですが、各社での予算一覧みたいなのがあったりします。
多少のばらつきはありますが、大体10,000万円が平均でその辺にまとまっていることがわかりますね。
ですが、これを例えば、軸の最小値を6,000万円とかに設定すると下記のようなグラフに変わります。
はい、見ての通り圧倒的な格差が生まれますね。
そう、軸によって表現される尺度(スケール)が異なるので、視覚的に差が数字以上に広がるというものです。
その5:その他細かいもの寄せ集め
ここからはもう一々言及しなくても直感的に違和感を覚えそうなものを寄せ集めします。
いやもう5選じゃないじゃん。
推移を示す円グラフ
その3の例で書いた円グラフ。
割合を比較したいならば集団のスケールが同じ(=100%)ということですから、積み上げ棒グラフで示すほうがスッキリしたりします。
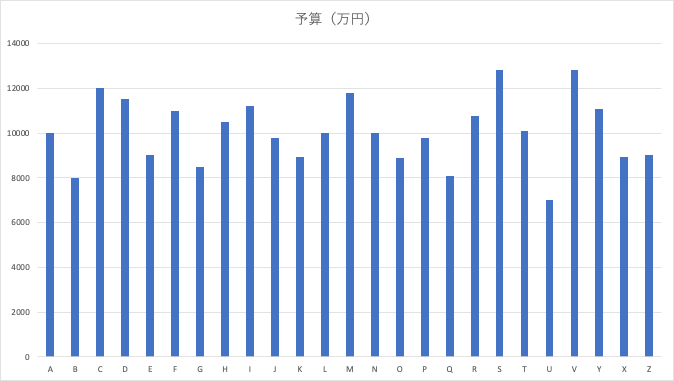
棒が多すぎる棒グラフ
一言で言います。項目がわからない・・・。
いらないデータは削りましょう・・・。
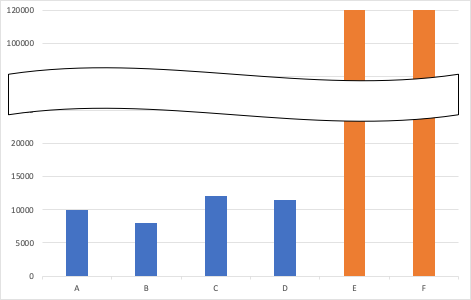
極端に値が大きい棒グラフ
その4と類似したものですが、軸の途中を波ダッシュ(〜)で省略してスケーリングが変なことになっているものもあります。
懐かしの波田陽区でいうところの「いや、結局正確に捉えられませんから!!残念!!スケール違い斬り!!!」っていうやつ。
がしかし、こちらについては最近は長年の統計教育の成果2もあってかかなり減ってきたように思います。いや、そうでもないか。
系列が多すぎる折れ線グラフ
ごちゃごちゃしていてもうわけわかめな状態のやつ。
説明に影響がない系列は消し去ってしまいましょう。
無意味な対数化
軸の値を表現する際に対数化というものがあります。
対数とは高校数学で習う、$log$で表現するアレ。Excelの機能だと底を選べますが、底を10(常用対数)とした場合以下の値となります。
- 10の場合:$log_{10} 10 = 1$
- 100の場合:$log_{10} 100 = 2$
- 100,000の場合:$log_{10} 100000 = 5$
いかがでしょうか?桁が圧倒的に違うのに、なんか大した差がない数字になりますね。
ちなみに高校数学の復習ですが底を10とした対数をとった場合、
$N$ が $n$ 桁の数
$ \Leftrightarrow 10^{n−1} \leqq N < 10^n$
$ \Leftrightarrow n−1 \leqq log_{10} N < n$
となります。
おまけ:各グラフの意味と表現例
基本的には、グラフで何かを表現する際は書きを意識すると良いでしょう。
円グラフ
ある集団の中での割合を表現する際に使えます。
簡単な例だと、ある集団における出身地(北海道・東北・関東・中部・近畿・中国・四国・九州)を示したときとか。
棒グラフ
同じ尺度の観測値を比較したい際に使えます。
簡単な例だと、12月時点での主要携帯キャリアの顧客純増数とか。
折れ線グラフ
時系列等の傾向を可視化する際に使えます。また、棒グラフだと表現が難しい多数の時点と観測値を表現することも可能です。
簡単な例だと、株価の推移ですね。
最後に
いかがでしたでしょうか。「あ〜これよく見る」というものもあるかと思います。もしかしたら「最近作ってしまった・・・」ということもあるかと思います。でも大丈夫、人は失敗して成長するもの。これから気をつけてばいいだけの話だと思います。
ちなみにですが誤解を与えないグラフを作る観点としては、「客観的な結果を示しているか(主観を組み込んでいないか)」、「数字とグラフを見比べて違和感がないか」ということかなと考えています。
まだまだ私も修行の身ですが、きれいなグラフを作られるように頑張っていきましょう。
Enjoy!
参考文献
- ダレル・ハフ; 高木秀玄. 統計でウソをつく法. 講談社, 1968.
- 東京経済大学経済学部 黒田敏史. 経済統計a:第八回. 最終閲覧日:2020年12月13日.http://web.tku.ac.jp/~kuroda/econstat8.pdf
- ito_yan110. 絶対に描いてはいけないグラフ入りスライド24枚 Jpana.R 2014. 最終閲覧日:2020年12月13日.https://www.slideshare.net/itoyan110/24-44156981
- Tableau. グラフの種類と使い方、間違った使われ方. 最終閲覧日:2020年12月13日.https://www.tableau.com/ja-jp/learn/articles/graph-type
- 一般社団法人データサイエンティスト協会. データサイエンティストのスキルレベル 2019年版. 最終閲覧日:2020年12月13日.https://www.datascientist.or.jp/common/docs/skilllevel_cps.pdf