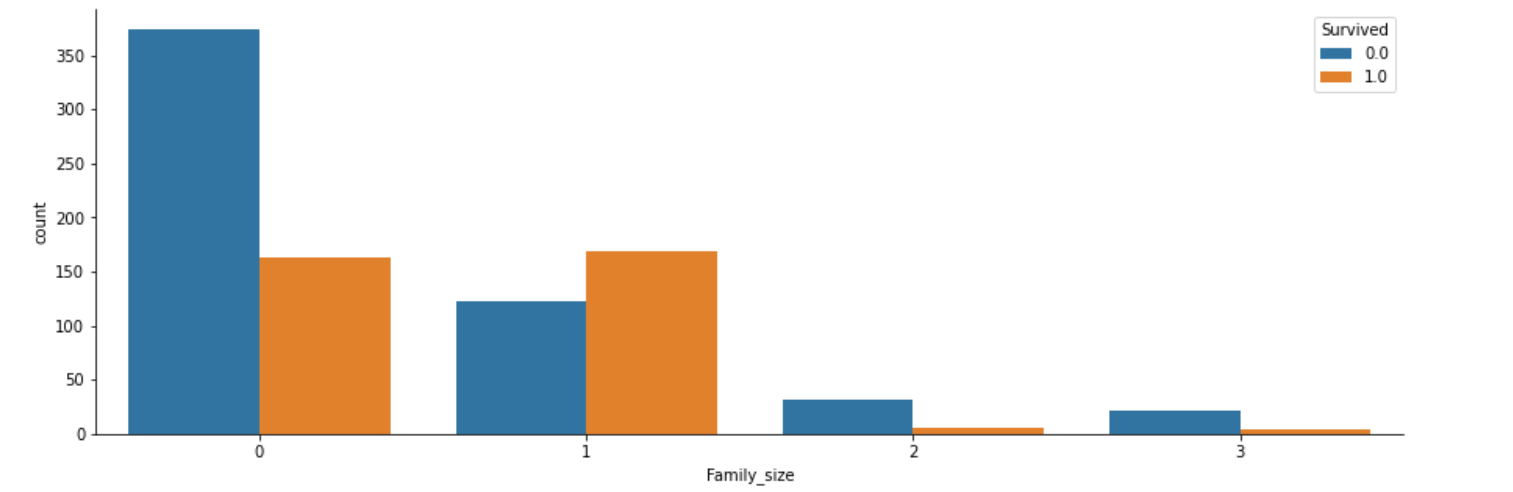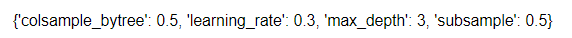Kaggle Titanic Score-80.8%までの道のり

#はじめに

Kaggleのtitanicコンペに挑戦しました。
最初は、右も左もわからず平均スコア（75%）でしたがコードを改善し、80.8%までスコアアップさせることができました。

今回は、スコア80.8%までの道のりをデータ同士の関係を見ながら、どのようにスコアを上昇させたのかを紹介します。

＜記事の流れ＞

• データ分析の流れを紹介
• 80.8%のコードをグラフなどを使用して説明
• 全体のコード紹介
• ベースラインからどのように改善したのか
• 精度改善にどんな手法が有効、もしくは無効だったのか
• 今後取り組むべき課題
• まとめ

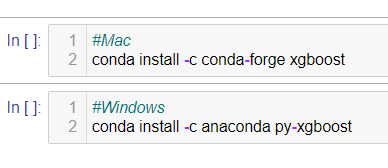
この記事では、xgboostをメインにモデルを実装していくので、importする前にxgboostのインストールを行ってください。インストール方法は、OSに応じて、以下のコードを実行してください。

それでは、データ分析の流れを紹介します。

#データ分析の流れ（改善前）
1.データセットを読み込み、概要を確認
2.データの欠損値を確認
3.欠損値補完
4.ラベルエンコーディンング
5.目的変数と説明変数の相関関係をグラフ化
6.モデル学習に用いる説明変数を選別
7.モデル構築（ランダルフォレスト使用）
8.モデル学習をして、テストデータを使って正解ラベルを予測
9. 予測結果を提出の形にして、csvファイルに保存
10.提出(submit)

#データ分析の流れ（改善後スコア80.8%）

1.仮説を立てる
2.訓練データ、テストデータの結合
3.データの概要と欠損値の確認
4.仮説をもとにそれぞれの説明変数をグループ分けして、欠損値を補完
5.ラベルエンコーディング
6.Family_size説明変数を作成
7.仮説をもとに、説明変数を作成（家族について深堀）
8.最後の前処理（説明変数選別、ダミー変数化、標準化、学習できるデータに変換）
9.モデルを構築し、学習を行い、テストデータに対して予測を行う（決定木, xgboost）
10.予測結果を提出の形にして、csvファイルに保存
11.提出（submit）

次に、スコア80.8%達成したコードをグラフなどを使用して説明します。

#スコア80.8%コードの詳細

##1.仮説を立てる
合計6回仮説を立てて、モデルの性能を向上させました。

仮説1：目的変数との相関関係から、何かわかるのでは？
検証結果：目的変数"Survived"に対して、"Sex"と"Pclass"の相関係数の値が、それぞれ0.54, -0.34と、他に比べ大きくなっていることが確認できた。

仮説2：敬称ごとの生存率を調べれば、男女の生存関係が見えてくるのでは？
検証結果：男性の生存率は20%もなく、男の子の場合は約60%、女性（または女の子）の場合は約70%以上を確認できた。

仮説3：家族の人数によって、生存率が異なるのでは？
検証結果：独り身と、中家族、大家族の生存率が30%以下。小家族の生存率は50%以上。

仮説4：性別と年齢、家族数でグループ分けすることで、具体的な生存率が見えてくるのでは？
検証結果：家族数に関しては、仮説3の検証結果と同じだったが、
男性の場合、子どもかつ小家族であれば生存率が67%と、他に比べて圧倒的に高く、女性の場合、年齢関係なく生存率が70%以上を確認できたが、家族数が多いと生存率が40%以下であることが確認できた。

仮説5：客室等級が高いほど、生存率が上がるのでは？
検証結果：男性の場合、全体的に生存率が低いため何とも言えないが、女性の場合、上位の等級（Pclass1, 2）では80%以上の生存率が確認でき、一番下の等級との生存率の差は歴然としていた。

仮説6：スコアを上昇するために、標準化を行い、データのスケールをそろえる必要があるのではないか？
検証結果：ここでやっと、スコア79%から80.8%達成。

以下では、最初の仮説から、仮説6までを流れに沿ってコードを紹介します。

##2.訓練データ、テストデータの結合

はじめに、importしたライブラリの紹介をします。

#使用するライブラリ
import numpy as np 
import pandas as pd 
import seaborn as sns
import matplotlib.pyplot as plt
import xgboost as xgb
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score

改善前では、trainデータとtestデータを別々に扱っていたのですが、欠損値をそろえるために結合します。

#データの読み込み
train = pd.read_csv("titanic/train.csv")
test = pd.read_csv("titanic/test.csv")

#indexを"PassengerId"に設定
train = train.set_index("PassengerId")
test = test.set_index("PassengerId")

#train, testデータの結合
df = pd.concat([train, test], axis=0, sort=False)
df

このように、DataFrameとして結合したデータを確認できます。

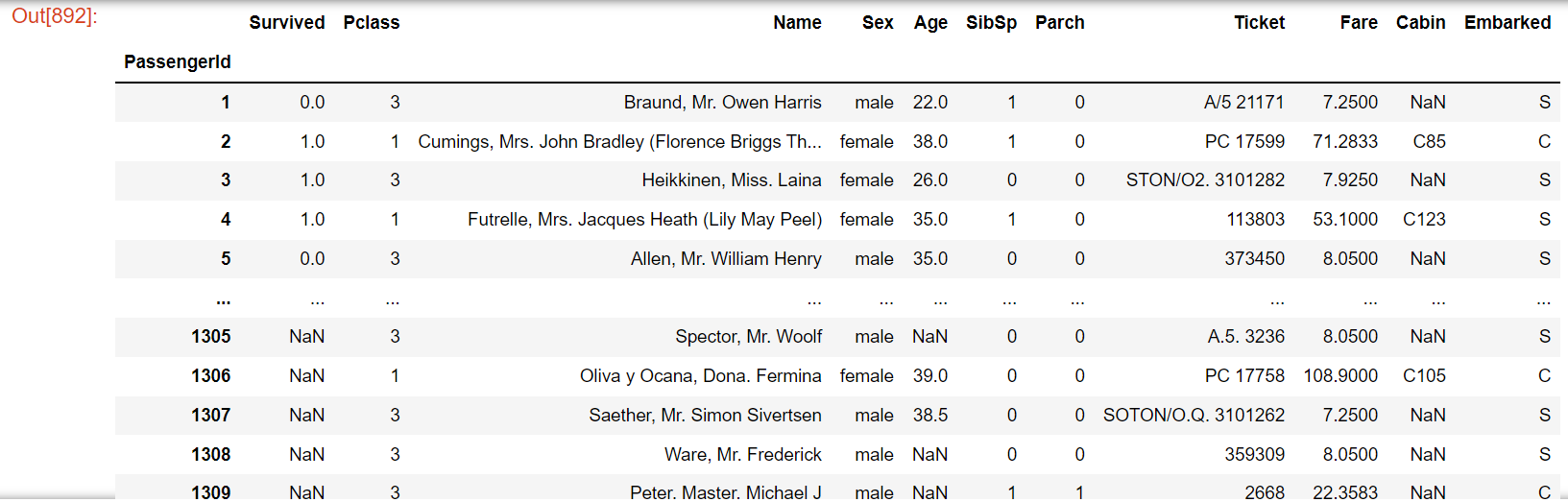
＜説明変数（特徴量）の概要＞

• PassengerId – 乗客識別ユニークID
• Survived – 生存フラグ（0=死亡、1=生存）
• Pclass – 客室等級
• Name – 乗客の名前
• Sex – 性別（male=男性、female＝女性）
• Age – 年齢
• SibSp – タイタニックに同乗している兄弟/配偶者の数
• parch – タイタニックに同乗している親/子供の数
• ticket – チケット番号
• fare – 料金
• cabin – 客室番号
• Embarked – 出港地（タイタニックへ乗った港）

※カテゴリー変数の概要

Pclass
1 = 1等ファーストクラス（上流階級）
2 = 2等セカンドクラス（中流階級）
3 = 3等サードクラス（労働階級）

Embarked
C = Cherbourg
Q = Queenstown
S = Southampton

##3.データの概要と欠損値の確認

#データの概要を確認
df.info()

• Int64Index：1309行（インデックス）データが並んでいることを確認できます。
• Column：説明変数（カラム名）を確認できます。
• Non-Null Count：説明変数ごとの欠損値の数を確認できます。
• Dtype：説明変数ごとのオブジェクトの型を確認できます。　

（Dtypeがobjectとなっている場合は、説明変数のデータに文字列型や数値型などが混ざっていることを表します）

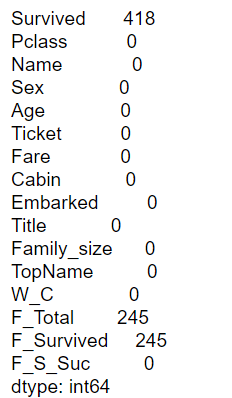
#欠損値を確認
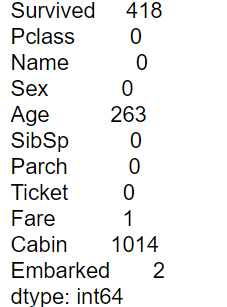
df.isnull().sum() 

ここでは、Survived, Age, Fare, Cabin, Embarkedに欠損値があることが確認できました。

##4～6.仮説をもとに欠損値を補完し、ラベルエンコーディングを行い、Family_sizeという新たな説明変数を作成
まずは、前処理が楽な"Sex"だけ、簡単にラベルエンコーディングしていきます。
そして、仮説1で立てたように、目的変数との相関関係を見ていきます。

###Sex

• 処理の流れ
• ラベルエンコーディング
• 目的変数との相関関係をグラフ化

まずは、性別をラベルエンコーディングします。
例）"female"→１, "male"→0

#"Sex"ラベルエンコーディング
df["Sex"] = df["Sex"].map({"female":1, "male":0})

#相関関係を調査
fig, axs = plt.subplots(figsize=(10, 8))
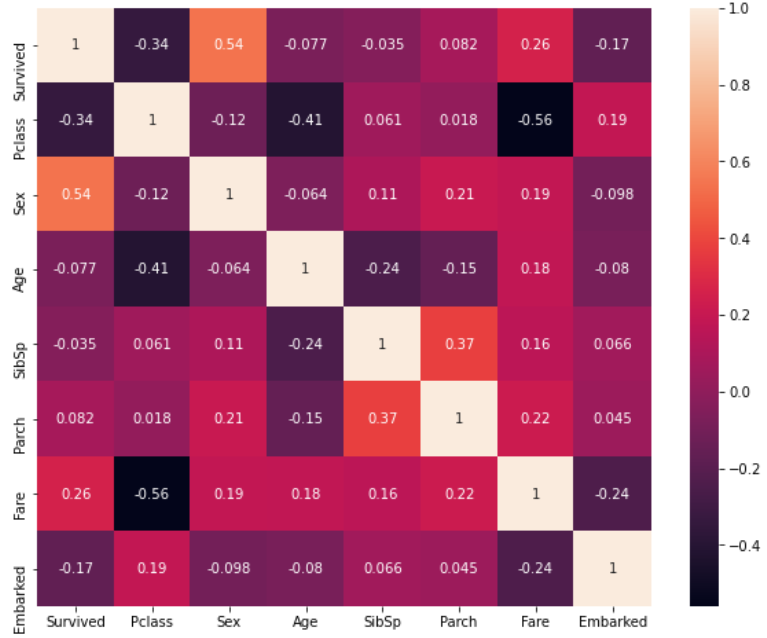
sns.heatmap(df.corr(),annot=True)
plt.show()

目的変数との相関を見たときに、他の説明変数に比べて、"Sex"は、正の相関が出ていて（0.54）、
"Pclass"は、負の相関（-0.34）が出ていることがわかりました。
また、"Fare"もほかの説明変数に比べて、正の相関が出ているようにも思えます（0.26）。

"Pclass"を基準に、各説明変数との相関係数を見ると、"Age"と"Fare"が比較的、負の相関が出ていることが確認できます。

男性に比べて女性の生存率の方が高い傾向がありそうです。
また、乗客の年齢と運賃が上がるにつれて、等級が上がり（Pclass3からPclass1に）、等級が上がるにつれて生存率が高くなることが予想できます。

###Embarked

• 処理の流れ
• ラベルエンコーディング
• 欠損値処理

Embarkedには欠損値があったので、ラベルエンコーディングを行い数値化したうえで、中央値で欠損値を補完していきたいと思います。

Sexと同じように、

#"Embarked"ラベルエンコーディング
#set(df["Embarked"]) {'C', 'Q', 'S', nan}
df["Embarked"] = df["Embarked"].map({"C":0, "Q":1, "S":2})
#Embarked欠損値補完
df["Embarked"] = df["Embarked"].fillna(df.Embarked.median())

###Age

• 処理の流れ
• グループ分けを行い欠損値処理
• グラフ化
• 4等分
• ラベルエンコーディング
• 割合グラフ化

仮説1の検証結果から、性別と等級が大きく生存に関係していることが考えられそうなので、df.groupbyメソッドを使用してDataFrameを"Pclass"と"Sex"でグループ分けした、"Age"の平均値で欠損値を補完します。

そのため、改善前のコードに比べより具体的なデータの値で欠損値を補完していることになります。
欠損地の補完ができたら、グラフ化します。

#"Age"欠損値補完
df["Age"] = df["Age"].fillna(df.groupby(["Pclass","Sex"])["Age"].transform("mean"))

#"Age"可視化
fig, axes = plt.subplots(figsize=(10, 5))
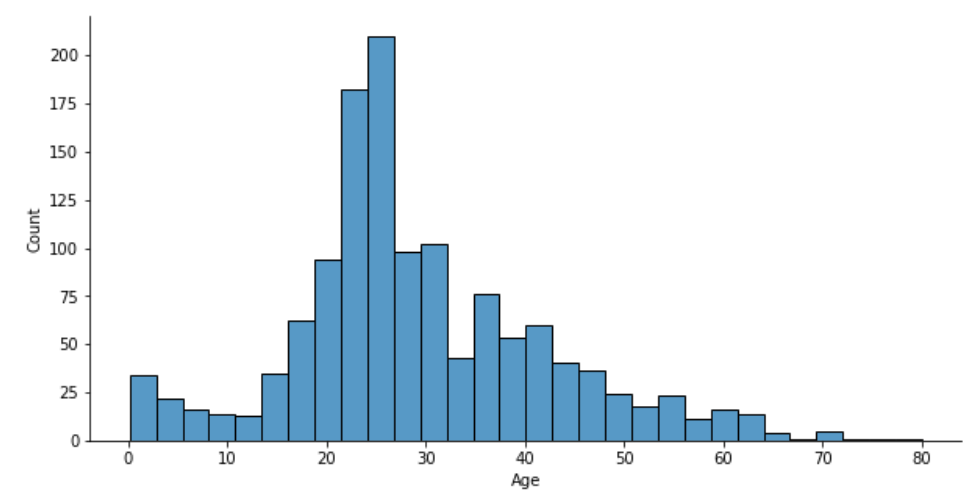
sns.histplot(data=df, x="Age")
sns.despine()

グラフを４等分して各年齢ごとの人数と、各年齢ごとの生存関係を見ていきます。

#4分割
cut_Age = pd.cut(df["Age"], 4)

#"Survived"との比較
fig, axs = plt.subplots()
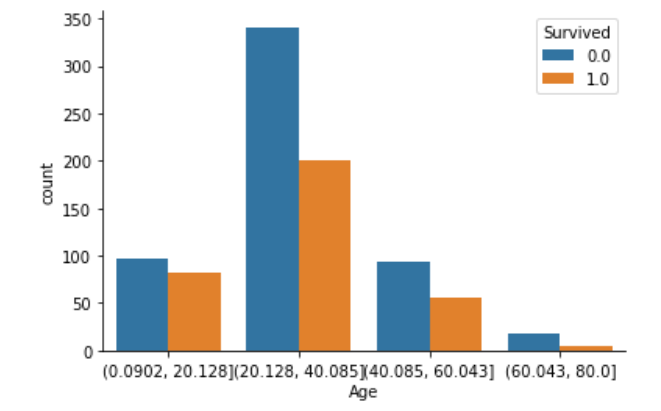
sns.countplot(x=cut_Age, hue="Survived", data=df)
sns.despine()

このグラフからは、データを読み取ることが難しそうです。
そのため、ラベルエンコーディングした後に、グラフを割合表示します。
まずは、ラベルエンコーディングです。

#"Age"ラベルエンコーディング
df["Age"] = LabelEncoder().fit_transform(cut_Age) 

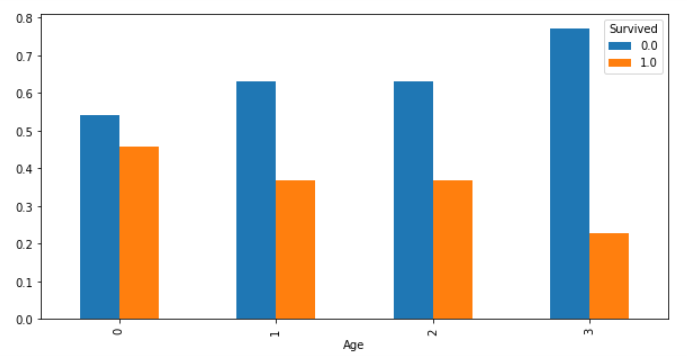
ラベルエンコーディングが済んだので、"Age"における"Survived"の割合を、グラフで表示します。
各棒グラフでは、Survivedの値（0, 1）が、合計100%（縦軸1.0）になるように表示します。

#pandasからグラフ表示（割合）
cross_Age = pd.crosstab(df["Age"], df["Survived"], normalize='index')
cross_Age.plot.bar(figsize=(10, 5))

年齢が若いほど、生存できる割合が50%に近づいているように見えます。
若い人の方が、体力があるから、このような結果になったのではないでしょうか。

###Fare

"Fare"も"Age"と同じ流れで処理していきます。

• 処理の流れ
• グループ分けを行い欠損値処理
• グラフ化
• 4等分
• ラベルエンコーディング
• 割合グラフ化

#"Fare"欠損値補完
df["Fare"] = df["Fare"].fillna(df.groupby(["Pclass", "Sex"])["Fare"].transform("median"))

#4分割
cut_Fare= pd.cut(df["Fare"],4)

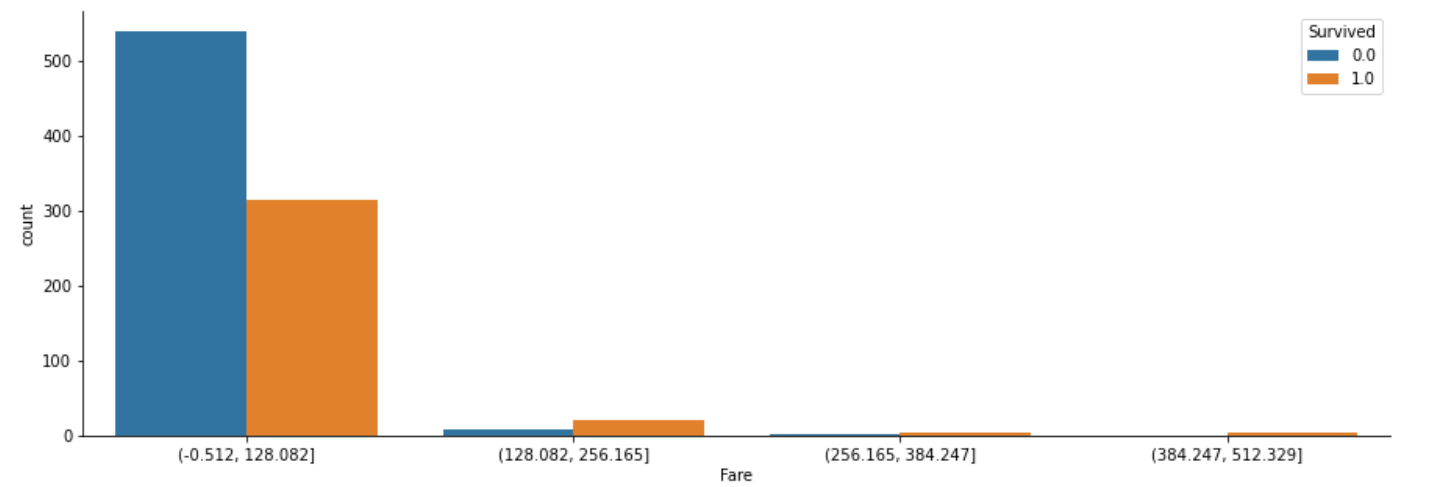
#"Survived"との比較
fig, axes = plt.subplots(figsize=(15, 5))
sns.countplot(x=cut_Fare, hue="Survived", data=df)
sns.despine()

このグラフからは、データを読み取ることが難しそうです。
そのため、ラベルエンコーディングした後に、グラフを割合表示します。
まずは、ラベルエンコーディングです。

#"Fare"ラベルエンコーディング
df["Fare"] = LabelEncoder().fit_transform(cut_Fare) 

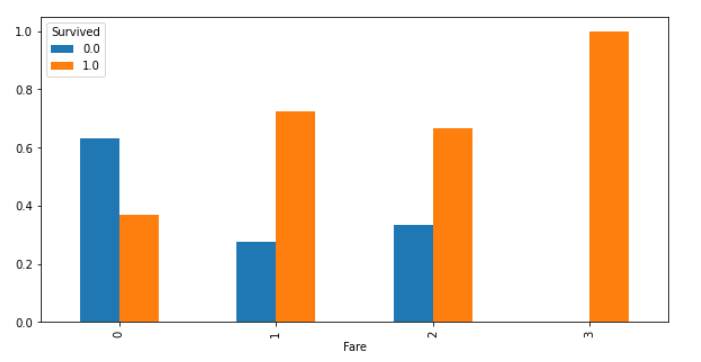
"Age"と同じく、ここでも"Fare"における"Survived"の割合を見ていきます。
各棒グラフでは、Survivedの値（0, 1）が、合計100%（縦軸1.0）になるように表示します。

#pandasからグラフ表示（割合）
cross_Age = pd.crosstab(df["Fare"], df["Survived"], normalize='index')
cross_Age.plot.bar(figsize=(10, 5))

運賃が高いと（0以外）、生存の割合が高いことを確認しましたが、上のグラフからわかるように、０グループ以外の人数が極端に少ないので何とも言えなさそうです。

###Cabin

• 処理の流れ
• データの先頭を文字列で取得
• カテゴリー変数ごとに生存関係を調査
• ラベルエンコーディング

"Cabin"は先頭（インデックス0番目）を文字列で取得し、カテゴリー変数（データ）の種類を見ていきます。
そして、カテゴリー変数ごとの生存率を調査し、生存率ごとにラベルエンコーディングしていきます。

#"Cabin"の欠損値補完と数値化
df["Cabin"] = df["Cabin"].apply(lambda x: str(x)[0])
set(df["Cabin"]) #{'A', 'B', 'C', 'D', 'E', 'F', 'G', 'T', 'n'}

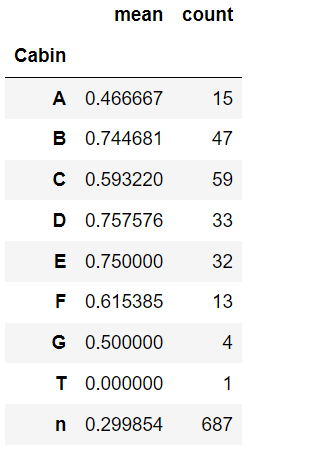
#"Cabin"ごとの"Survived"を確認
df.groupby(df["Cabin"])["Survived"].agg(["mean", "count"])

Cabinについては、データからわかるように、欠損値（687）が多過ぎることから、データの特徴をつかみにくいことが考えられるので、機械学習には使用しないことにします。

#"Cabin"ラベルエンコーディング
df["Cabin"] = LabelEncoder().fit_transform(df["Cabin"]) 

###Title（Name）

• 処理の流れ
• 敬称を取得
• 敬称を4種類にまとめる
• グラフ化
• ラベルエンコーディング

ここでは、敬称ごとの生存率を調べれば、男女の生存関係が見えてくるのではないか、
という仮説2を検証するために、"Name"の各データから敬称を取得して、新しい説明変数"Title"を作成します。

まずは、"Name"の各データの敬称の種類を調査します。
そして、敬称ごとの生存の平均を見ていき、グラフ化してラベルエンコーディングします。

#敬称の種類確認
df["Title"] = df.Name.str.extract("([A-Za-z]+)\.", expand = False)
df["Title"].value_counts()

敬称の種類を確認できたので、4種類にまとめます。

#4種類の敬称にまとめる
other = ["Rev","Dr","Major", "Col", "Capt","Jonkheer","Countess"]

df["Title"] = df["Title"].replace(["Ms", "Mlle","Mme","Lady"], "Miss")
df["Title"] = df["Title"].replace(["Countess","Dona"], "Mrs")
df["Title"] = df["Title"].replace(["Don","Sir"], "Mr")
df["Title"] = df["Title"].replace(other,"Other")

#敬称ごとの生存率を確認
df.groupby("Title").mean()["Survived"]

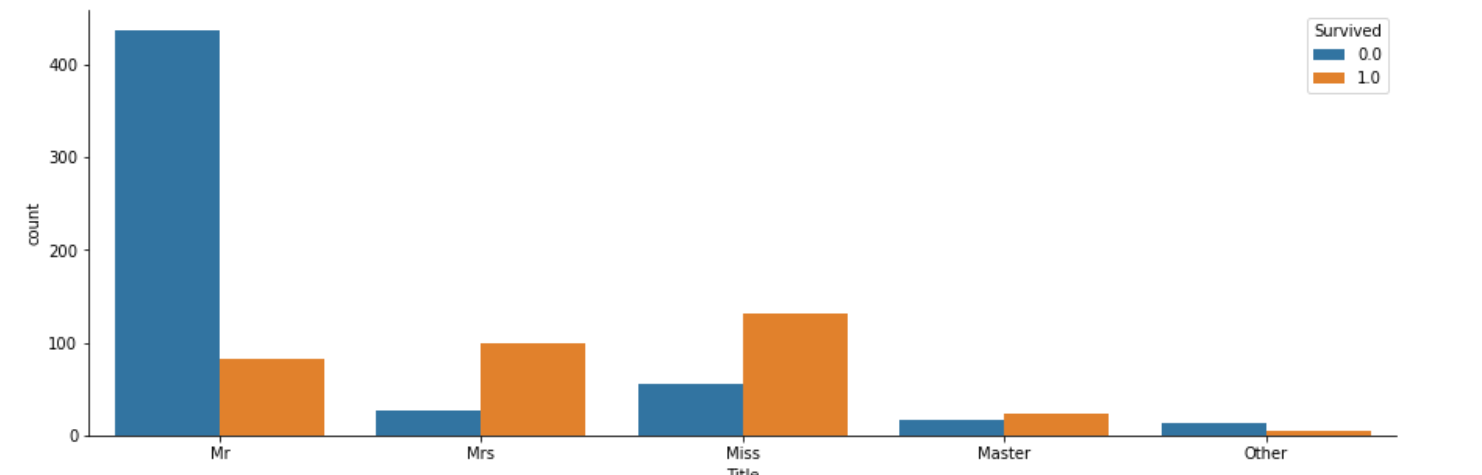
#敬称ごとの生存関係をグラフ化
fig, axs = plt.subplots(figsize=(15, 5))
sns.countplot(x="Title", hue="Survived", data=df)
sns.despine()

このことを深堀するため、ラベルエンコーディングを行った後に、"Title"における"Survived"の割合をグラフで表示します。

#"Title"ラベルエンコーディング
df["Title"] = LabelEncoder().fit_transform(df["Title"]) 
#{"Mr":2, "Mrs":3, "Miss":1, "Master":0, "Other":4}

ラベルエンコーディングによって、辞書順で、
"Mr":2, "Mrs":3, "Miss":1, "Master":0, "Other":4、にそれぞれラベル付けされました。
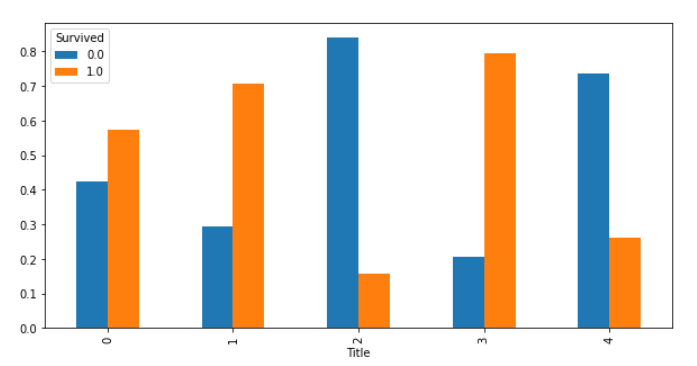
これをもとに、"Title"における"Survived"の割合をグラフで表示します。
各棒グラフでは、Survivedの値（0, 1）が、合計100%（縦軸1.0）になるように表示します。

#pandasからグラフ表示（割合）
cross_Age = pd.crosstab(df["Title"], df["Survived"], normalize='index')
cross_Age.plot.bar(figsize=(10, 5))

"Miss"や"Master"の敬称について、気になったので調べました。

当時の成人年齢が21歳なので、
・Miss：未婚の女性につける（21歳以下も含まれる）
・Master：未成年の男性につける
とのことで、Masterにいたっては男の子（全員）に付けている敬称ということです。

この情報をもとに、グラフを見てみると、女性と子どもの敬称（"Mrs":3, "Miss":1, "Master":0）であれば、生存率がほとんど60%以上あることがわかります。

つまり、女性または子どもであれば生存率が高いのではないかと予測できます。

###Family_size

ここでは、仮説3の家族の人数によって、生存率が異なるのではないか、について検証するため、
改善前のコードでは作成していなかった、説明変数"Family_size"を新たに作成します。
"Family_size"とは、"SibSp"と"Parch"と自分を合わせた家族数を表す説明変数です。

• 処理の流れ
• Family_size作成→グラフ化
• 家族数ごとにラベルエンコーディング
• グラフ化

#"Family_size"作成
df["Family_size"] = df["SibSp"] + df["Parch"]+1
#"SibSp", "Parch"をDataFrameから削除
df = df.drop(["SibSp","Parch"], axis = 1)

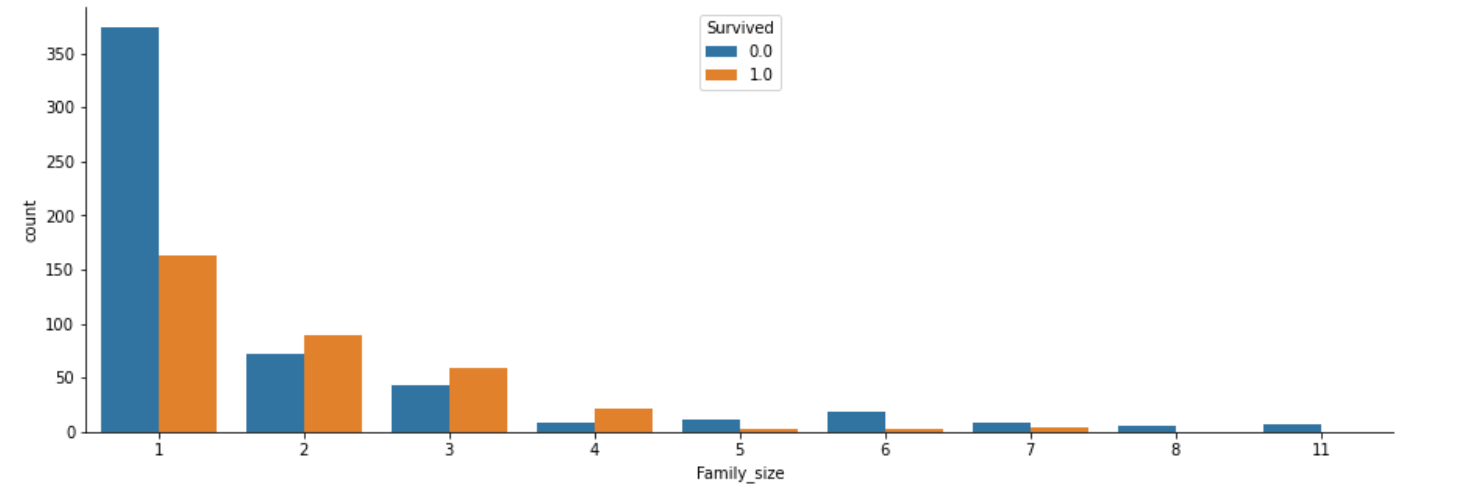
#家族数ごとの生存関係をグラフ化
fig, axs = plt.subplots(figsize=(15, 5))
sns.countplot(x="Family_size", hue="Survived", data=df)
sns.despine()

#"Family_size"ラベルエンコーディング
df.loc[ df["Family_size"] == 1, "Family_size"] = 0                            # 独り身
df.loc[(df["Family_size"] > 1) & (df["Family_size"] <= 4), "Family_size"] = 1  # 小家族 
df.loc[(df["Family_size"] > 4) & (df["Family_size"] <= 6), "Family_size"] = 2  # 中家族
df.loc[df["Family_size"]  > 6, "Family_size"] = 3                             # 大家族  

ラベルエンコーディングを行ったので、再びデータを確認（グラフ化）します。
"Family_size"と"Survived"の関係を、グラフで表示します。
その後に、"Family_size"における"Survived"の割合をグラフで表示します。
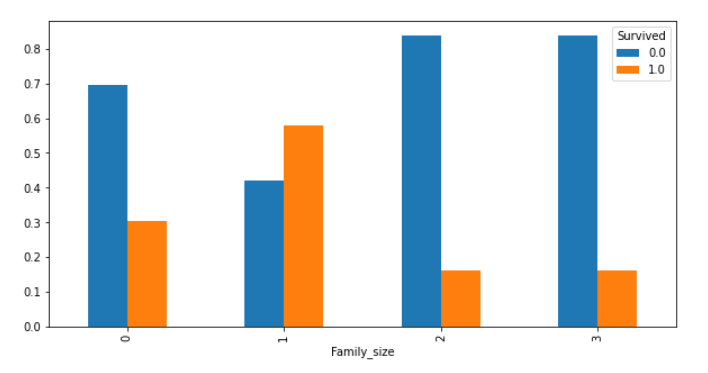
各棒グラフでは、Survivedの値（0, 1）が、合計100%（縦軸1.0）になるように表示します。

#"Family_size"の生存率をグラフ化
fig, axs = plt.subplots(figsize=(15, 5))
sns.countplot(x="Family_size", hue="Survived", data=df)
sns.despine()

#pandasからグラフ表示（割合）
cross_Age = pd.crosstab(df["Family_size"], df["Survived"], normalize='index')
cross_Age.plot.bar(figsize=(10, 5))

２人以上４人以下の家族（小家族）だけ、生存できる割合が50%以上あることがわかります。
独り身や、家族数が多くても助かる確率は低そうですね（どれも30%未満なので）。

家族が多すぎると身動きが取りにくく、逆に独り身だと、家族とともに乗船した人より、生き残ろうと思う気持ちが弱かったのではないでしょうか。
つまり、家族数も生存に関係していそうだと予測できます。

###Ticket

• 処理の流れ
• 数字の部分だけを取得
• データ型を"int64"に変換

"Ticket"の数字だけを取得し、データ型を"int64"に変換します。

#"Ticket"は数字の部分だけを取得しデータ型をint64に変換
df["Ticket"] = df.Ticket.str.split().apply(lambda x : 0 if x[:][-1] == "LINE" else x[:][-1])
df.Ticket = df.Ticket.values.astype("int64")

##7.仮説をもとに説明変数を作成（家族データについて深堀）

ここまでで、"Survived"（目的変数）に最も関係していそうな説明変数は
"Sex", "Pclass", "Age", "Family_size"ではないかと予想できるので、これらの説明変数をグループ分けして、生存率との関係を深堀していきます。

ここからは、仮説4と仮説5を検証していきます。

まずは、"Pclass"以外で生存関係を見ていきます。
以下のデータでは、3つの変数でグループ分けを行い、生存率と、生と死を合わせた総人数を表しています。

#3つの変数をグループ分けして生存率と、生と死を合わせた総人数を調査
s_mean = df.rename(columns={"Survived" : "S_mean"})
s_count = df.rename(columns={"Survived" : "S_count"})

s_mean = s_mean.groupby(["Sex", "Age", "Family_size"]).mean()["S_mean"]
s_count = s_count.groupby(["Sex", "Age", "Family_size"]).count()["S_count"]

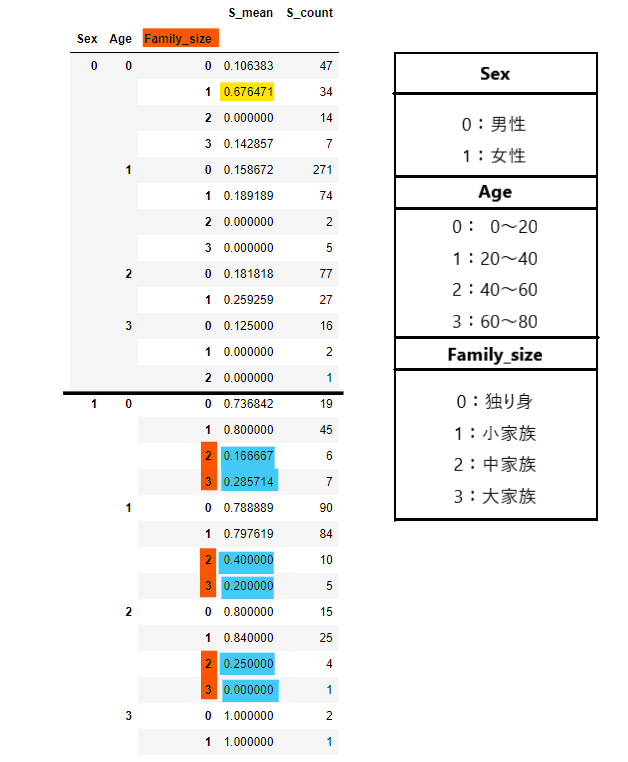
pd.concat([s_mean, s_count], axis=1)

小家族で20歳未満の男の子だけ生存率が高いですね（黄色マーカー）。
また、女性は家族数が多いと生存率が低くなっているのが分かります（青色マーカー）。

次は、"Pclass"も含めて性別ごとにデータを見ていきます。

#4つの変数をグループ分けして生存率と、生と死を合わせた総人数を調査（男性）
m_s_mean = df.rename(columns={"Survived" : "S_mean"})
m_s_count = df.rename(columns={"Survived" : "S_count"})

m_s_mean = m_s_mean.groupby(["Sex", "Age", "Family_size", "Pclass"]).mean().head(29)["S_mean"]
m_s_count = m_s_count.groupby(["Sex", "Age", "Family_size", "Pclass"]).count().head(29)["S_count"]

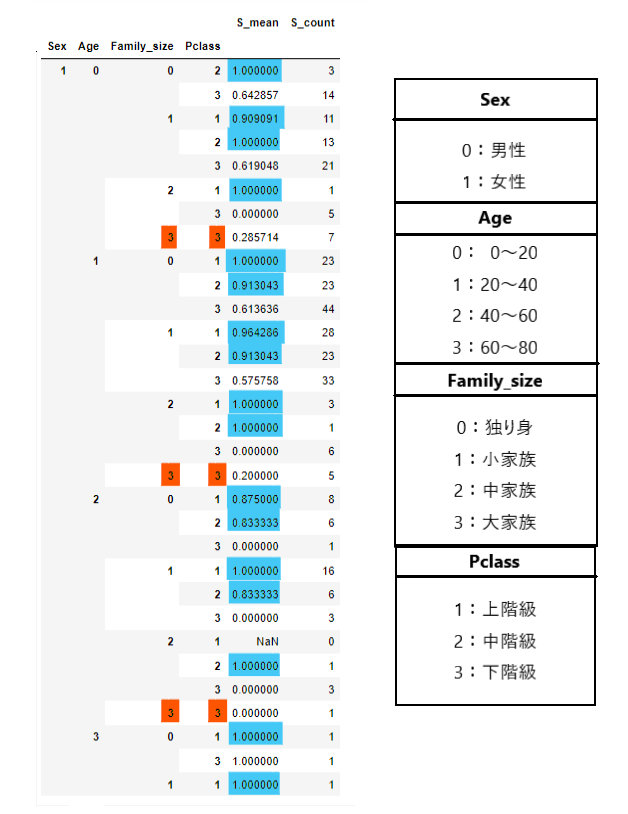
pd.concat([m_s_mean, m_s_count], axis=1)

具体的にデータが分かってきました。
男性の場合、一部だけ（黄色マーカー）生存率が高いことが確認できます。ですが、生と死を合わせた総人数（緑マーカー）からわかるように、値が少ないためノイズの可能性も考えられます。

#4つの変数をグループ分けして生存率と、生と死を合わせた総人数を調査（女性）
w_s_mean = df.rename(columns={"Survived" : "S_mean"})
w_s_count = df.rename(columns={"Survived" : "S_count"})

w_s_mean = w_s_mean.groupby(["Sex", "Age", "Family_size", "Pclass"]).mean().tail(31)["S_mean"]
w_s_count = w_s_count.groupby(["Sex", "Age", "Family_size", "Pclass"]).count().tail(31)["S_count"]

pd.concat([w_s_mean, w_s_count], axis=1)

女性の場合、年齢関係なく生存率が高いです。
各データを見ていくと、大家族には一番低い客室等級を使用している人しかいません（オレンジのマーカー以外）。
また、オレンジ色のマーカーのところはすべて生存率が低いです（30%以下）。

この２つのデータの共通点として、家族についての情報が生存関係と大きくかかわってくるのではないか、と考えられるため、これらのデータをさらに深掘りしていきます。
なので、女性または子どもの家族の生存率を取得するため、説明変数"F_S_Suc"を作成します。

女性と子どもの家族の生存率を表す説明変数"F_S_Suc"を作成

• 処理の流れ
• 苗字を取得
• 女性または子どものデータをTrue
• 取得したデータから家族の生存率をもとめる
• 家族の生存率ごとの女性または子どもの生存率を調査
• 計算で使用した説明変数を削除

#"Name"の最初を取得
df["TopName"] = df["Name"].map(lambda name:name.split(",")[0].strip())

#女性または子どもはTrue
df["W_C"] = ((df.Title == 0) | (df.Sex == 1))

#女性または子ども以外はTrue
df["M"] = ~((df.Title == 0) | (df.Sex == 1))

#具体的な家族の生存データ
family = df.groupby(["TopName", "Pclass"])["Survived"]

df["F_Total"] = family.transform(lambda s: s.fillna(0).count())
df["F_Total"] = df["F_Total"].mask(df["W_C"], (df["F_Total"] - 1), axis=0)
df["F_Total"] = df["F_Total"].mask(df["M"], (df["F_Total"] - 1), axis=0)

df["F_Survived"] = family.transform(lambda s: s.fillna(0).sum())
df["F_Survived"] = df["F_Survived"].mask(df["W_C"], df["F_Survived"] - df["Survived"].fillna(0), axis=0)
df["F_Survived"] = df["F_Survived"].mask(df["M"], df["F_Survived"] - df["Survived"].fillna(0), axis=0)

df["F_S_Suc"] = (df["F_Survived"] / df["F_Total"].replace(0, np.nan))
df["F_S_Suc"].fillna(-1, inplace = True)

#女性または子ども(True)とそれ以外の人(False)の生存率と生と死を合わせた総人数を調査（家族の生存率ごと）
s_df = df.groupby(["F_S_Suc", "W_C"])["Survived"].agg(["mean", "count"])
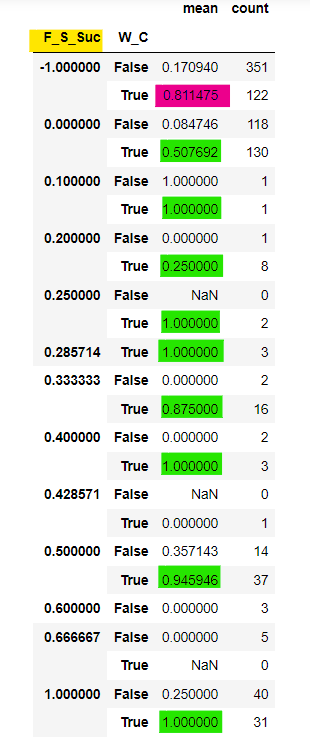
s_df

カラムに注目します。"F_S_Suc"は家族の生存率、"W_C"は女性または子どもであれば、Trueを表示しているのが確認できます（Falseであれば、男性）。
"F_S_Suc"が-1というのは、独身、家族と乗船していないことを表します。そこで、赤色マーカーに注目すると、80％以上の女性と子どもの生存率が確認できます。

また、家族の生存率（"F_S_Suc"）が増加するにつれて、女性または子どもの生存率が高くなることも確認できます。
家族が全員生存した場合だと、女性または子どもの生存率は100％です。

家族の生存率が0%ところを見ると、True, Falseの生存率は約50%、約0.08%であることから家族全員で一緒に死ぬことを選んだ人もいるのではないでしょうか。

最後に、計算に使用した説明変数を削除します。

#"F_S_Suc"の計算で使用した説明変数の削除
df.drop(["TopName", "W_C", "M", "F_Total","F_Survived"], axis = 1, inplace = True)

##8.最後の前処理（説明変数選別、ダミー変数化、標準化、学習できるデータに変換）

上記では、仮説の検証を行ってきましたが、
ここからは、検証結果をもとに、最後の前処理を行います。

• 処理の流れ
• 欠損値の確認
• 説明変数選別
• ダミー変数化
• 標準化
• 学習できるデータに変換（trainデータ, testデータに分割）

＜欠損値の確認＞
説明変数の欠損値を確認したいと思います。

#欠損値の確認
df.isnull().sum()

それでは、説明変数を選別していきます。

＜説明変数の選別＞

#説明変数選別
df["PassengerId"] = df.index
df.drop(["Name","Embarked","Title", "Cabin"], axis=1, inplace=True)

次に、説明変数のうち"Sex", "Pclass", "Fare"をダミー変数化します。

＜ダミー変数化＞
ダミー変数化（ワンホット表現）にする意味は、学習に使用する説明変数に大小関係の意味を持たせないためです。
drop_first=Trueとは、先頭のダミー変数を削除するというオプションです。"Sex"では、0が男性、1が女性なので、片方の説明変数がわかれば必然的にもう一つの変数もわかるので、ここでは、Trueにしました。

#ダミー変数化
df = pd.get_dummies(df, columns=["Sex"], drop_first=True)
df = pd.get_dummies(df, columns=["Pclass", "Fare"])

＜標準化＞
ここでは、最後の仮説である、スコアを上昇するために、標準化を行い、データのスケールをそろえる必要があるのではないか、について検証していきます。

例えば、年齢20で、身長が180のデータを考えた場合、20と180では180の方が学習に与える影響が大きいとモデルが解釈するため、標準化を行うことでそれぞれの説明変数のデータのスケールをそろえることにしました。

標準化を行うことで、データのスケールをそろえます。
実は、この標準化という最後の前処理がスコア80%の壁を乗り越えるための最も重要な処理になりました。

ここで、データを確認してみます。

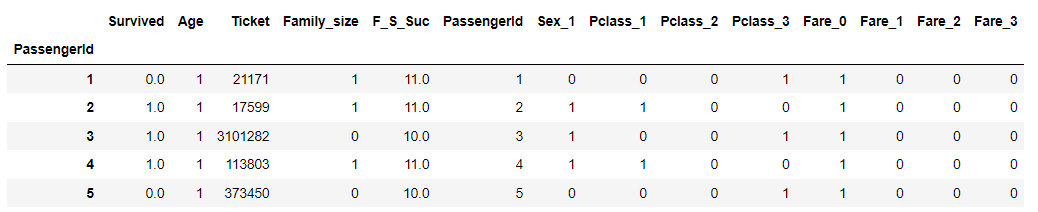
#DataFrame確認
df.head()

上記で説明した通り、"Ticket"だけスケールが大きいことが確認できます。
そのため、"Ticket"のみ標準化を行います。

#"Ticket"のみ標準化
num_features = ["Ticket"]

for col in num_features:
    scaler = StandardScaler()
    df[col] = scaler.fit_transform(np.array(df[col].values).reshape(-1, 1))

＜学習できるデータに変換＞
これまで、結合してデータの前処理を行っていたので、学習データとテストデータに分割して、モデルに学習させます。

#元の形に戻す（train, testデータの形に）
train, test = df.loc[train.index], df.loc[test.index]
#学習データ
x_train = train.drop(["PassengerId","Survived"], axis = 1)
y_train = train["Survived"]
train_names = x_train.columns
#テストデータ
x_test = test.drop(["PassengerId","Survived"], axis = 1)

##9.モデル学習を行いモデルを構築し、テストデータに対しての予測も行う（xgboostメイン）

• 処理の流れ
• 決定木を用いて、学習、説明変数の重要度を表示
• xgboostを用いて、学習、説明変数の重要度を表示
• 予測精度の比較

＜決定木＞
ここでは、グリッドサーチcvの結果をもとに、最適なパラメータを設定しています。

#決定木
decision_tree = DecisionTreeClassifier(random_state=0, max_depth=3)

#学習
decision_tree.fit(x_train, y_train)

#推論
y_pred = decision_tree.predict(x_train)

#正解率： 0.8125701459034792
print("正解率：", accuracy_score(y_train, y_pred))

#提出データ1
y_pred = decision_tree.predict(x_test)

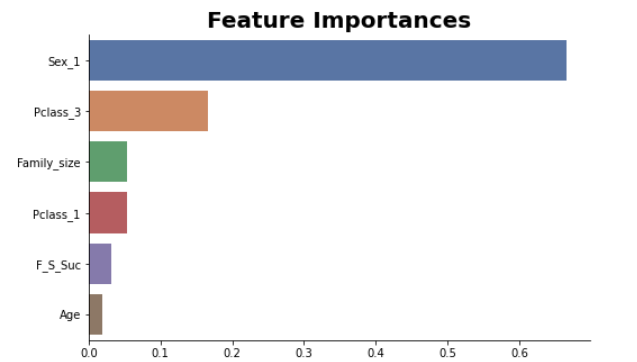
どの説明変数が学習に効いたのかをグラフで見ていきます。

#説明変数の重要度をグラフで表示（決定木）
importances = pd.DataFrame(decision_tree.feature_importances_, index = train_names)
importances.sort_values(by = 0, inplace=True, ascending = False)
importances = importances.iloc[0:6,:] 

plt.figure(figsize=(8, 5)) 
sns.barplot(x=0, y=importances.index, data=importances,palette="deep").set_title("Feature Importances",
                                                                                 fontdict= { 'fontsize': 20,
                                                                                            'fontweight':'bold'});
sns.despine()

これまでの分析では、性別、等級、家族に関する説明変数を中心に仮説を立ててきましたが、説明変数の重要度がわかるグラフの結果から、これらの説明変数が、学習に影響を与えていることがわかりました。そのため、女性が助かる可能性、上位等級の人が助かる可能性、また、家族に関するデータによって生存できるかどうかの予想ができることが考えられます。

＜xgboost＞
xgboostとは、GBDTの一種で、精度、計算測度、使いやすさに優れているため、最初に試すアルゴリズムとして有名です。また、Kaggleコンペの上位をGBDTで占めていることがよくあります。
今回は、GBDTの中でも古くから使用されており、資料も多いという理由で、xgboostを使用しました。

ここでは、グリッドサーチcvを行い、検証用データのスコアとKaggle提出のスコアをもとに、最適なパラメータを設定しています。

#xgboost
dtrain = xgb.DMatrix(x_train, label=y_train)
dtest = xgb.DMatrix(x_test)
#パラメータ
params = {'colsample_bytree': 0.5, 
         'learning_rate': 0.1, 
         'max_depth': 3, 
         'subsample': 0.9, 
         "objective":"multi:softmax", 
         "num_class":2}
#学習
bst = xgb.train(
    params, 
    dtrain, 
    num_boost_round=10)

#推論
y_pred_2 = bst.predict(dtrain)

#正解率： 0.8215488215488216
print("正解率：",accuracy_score(y_train, y_pred_2))

#提出データ2
y_pred_2 = bst.predict(dtest)

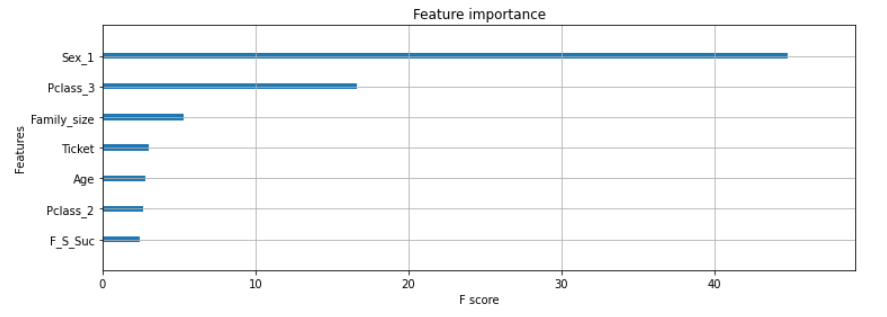
学習で、どの説明変数が重要だったのかを表示します。

#説明変数の重要度をグラフで表示（xgboost）
fig, ax = plt.subplots(figsize=(12, 4))

mapper = {'f{0}'.format(i): v for i, v in enumerate(train_names)}
mapped = {mapper[k]: v for k, v in bst.get_score(importance_type="gain").items()}

xgb.plot_importance(mapped,
                    ax=ax, 
                    show_values=False)
plt.show()

xgboostにおいても、決定木と同じことが考えられます。
xgboostは、決定木のアンサンブルなので、このグラフに納得できます。

＜予測精度の比較＞

【決定木】

• 正解率：81.2％

【xgboost】

• 正解率：82.1%

正解率を見ると、差はわずかですがxgboostの方が精度が高いことが確認できます。
また、決定木は過学習しやすいというデメリットもあるので、xgboostの方が信用できる精度であることが予想されます。
最後に、xgboost、決定木の予測結果をKaggleに提出します。

##10.予測結果を提出の形にし、csvファイルに保存

最後に、Kaggleに提出する形にしていきます。

Titanicコンペ参加時にダウンロードした"gender_submission.csv"ファイルの形で提出するように書かれていたので、そのファイルをもとに"PassengerId","Survived"の２つの列名からなるcsv形式のファイルを作成します。

#submit用のファイル１を作成(決定木)
submit = pd.DataFrame({"PassengerId":test["PassengerId"], "Survived":y_pred.astype(int).ravel()})
submit.to_csv("answer_xgb_2021_06_24.csv",index = False)

#submit用のファイル２を作成(xgboost)
submit = pd.DataFrame({"PassengerId":test["PassengerId"], "Survived":y_pred_2.astype(int).ravel()})
submit.to_csv("answer_tree_2021_06_24.csv",index = False)

データ分析の流れは以上になります。

＜予測精度の比較＞

【決定木】

• GridSearchCV

• 正解率：82％

• Kaggle_Score（提出結果）：75.5％

• パラメータ修正後

• 正解率：81.2％

• Kaggle_Score（提出結果）：75.3％

【xgboost】

• GridSearchCV

• 正解率：86%

• Kaggle_Score（提出結果）：78%

• パラメータ修正後

• 正解率：82.1%

• Kaggle_Score（提出結果）：80.8％

#全体のコード紹介

Git Hubにコードを載せているので、参考にしたい方は、下のURLをクリックしてみてください。

次に、ベースライン（スコア75%）からどのように改善したのかについて見ていきます。

#ベースラインからどのように改善したのか

ベースライン（スコア75%）からスコア80.8%に到達するまでに、改善したところ紹介します。

• 改善点
• 仮説を立てる
• train, testデータを結合し、欠損値補完の値を統一
• 欠損値補完方法をより具体的に
• ラベルエンコーディングの仕方を改善
• 説明変数のグループ化して、データの詳細を見る
• ダミー変数化、標準化を行う

順に説明します。

##仮説を立てる

冒頭では、最初の仮説として「目的変数との相関関係から、何かわかるのでは？」を記述しました。
なぜこのような仮説に至ったかというと、相関関係を見ることによって、因果関係は分からないものの、何かしらの関連性が見えることで、データを深堀するキッカケになるのではないかと思ったので、この仮説を最初に持ってきました。

その後分析の流れとしては、「仮説➡改善➡検証結果➡調査➡仮説」を繰り返しました。

##train, testデータを結合し、欠損値補完の値を統一した。

##欠損値補完方法をより具体的に

改善前とスコア80.8%の欠損値補完方法が異なるので、説明変数"Age"をもとに具体例を紹介します。

#"Age"欠損値補完（改善前）
x_test["Age"] = x_test["Age"].fillna(x_test["Age"].mean())

#"Age"欠損値補完（スコア82%）
df["Age"] = df["Age"].fillna(df.groupby(["Pclass","Sex"])["Age"].transform("mean"))

改善前では、列データの平均値で欠損値補完を行っています。

それに対し、スコア80.8%のコードではgroupbyメソッドとtransformメソッドを組み合わせて、より具体的な平均値で欠損値補完を行っています。

##ラベルエンコーディングの仕方を改善

改善前では、基本的にラベルエンコーディングを行っていませんでした。

それに対し、スコア80.8%のコードでは、LabelEncoderクラスのfit_transformメソッドを使用してカテゴリー変数に対して、ラベルエンコーディングを行っています。具体例を紹介します。

#"Title"のラベルエンコーディング
df["Title"] = LabelEncoder().fit_transform(df["Title"]) 

##説明変数をグループ化して、データの詳細を見る

groupbyメソッドを使用して、指定した説明変数同士をグループ分けしてデータの詳細を見ました。

#グルーピング
df.groupby(["Sex", "Age", "Family_size", "Pclass"]).mean().head(29)

##ダミー変数化、標準化を行う

ダミー変数化

#ダミー変数化
df = pd.get_dummies(df, columns=["Sex"], drop_first=True)
df = pd.get_dummies(df, columns=["Pclass", "Fare"])

標準化
正直、標準化を行うことでスコア80%を達成できたと言ってもいいです。

#"Ticket"のみ標準化
num_features = ["Ticket"]

for col in num_features:
    scaler = StandardScaler()
    df[col] = scaler.fit_transform(np.array(df[col].values).reshape(-1, 1))

次は、精度改善にどんな手法が有効、もしくは無効だったのかについて説明します。

#精度改善にどんな手法が有効、もしくは無効だったのか

• 精度改善に有効（有効度の高い順に）

• 標準化（79%→80.8%改善）

• ダミー変数化（平均スコア→79%改善）

• groupbyメソッド

• 欠損値補完でのgroupbyメソッドとtransformメソッドの合わせ技

• 精度改善に無効

• 相関関係だけを見て説明変数を選択

最後に、今後取り組むべき課題について考えていきます。

#今後取り組むべき課題

• データ分析に関するメソッドや関数を気軽に使用できること：

• データ分析に使用したメソッドなどの処理内容がわからないと、調べる時間が多くなり効率の悪さを感じました。
  また、メソッドなどの基本的な機能（引数や戻り値など）を知っていると応用が利くと感じました。

• 相関関係では見えない、目的変数と関係の強い特徴量を作成できる：

• 相関関係では見えない、目的変数との関係の強いデータを見つける（計算して作り出す）ことがスコアアップの鍵なので、データの重要なポイントを押さえることや、そこから説明変数を削除したり、新たに説明変数を作成する能力が低いと感じました。
  解決策として、データ分析を行うことで学んでいくという方法もありますが、いきなり応用だとなんとなくの知識しか入らないため、まずはデータ分析の参考書を読んで基礎知識を学習する必要があると感じました。

• 分析の流れをパターン化する（分析を行う際の考え方を学ぶ）：

• 上記で書いたデータの重要なポイントを押さえるという事にも繋がりますが、目的変数とのグラフの形がこうなっていればデータの関係性が強い傾向があるため削除せずに残しておこう、などデータ分析に対する知識の低さを感じました。
  解決策は上記と同じです。

• アルゴリズムの中身を理解して、状況からアルゴリズムを選別して学習に用いる：

• 今回のコンペは教師あり学習の分類タスクだったので、アルゴリズムの内容がわからないまま、なんとなくスコアが高くなる分類アルゴリズムを選択して学習モデルを構築しました。今後、機械学習を行っていくうえでなんとなくでアルゴリズムを選択してはまずいと思ったので、この課題に対しても対策として参考書などで、まずはアルゴリズムの概要から学習する必要があると感じました。

#まとめ

以上が、Kaggle Titanic Score 80.8%までの道のりでした。
このコードを参考に、Kaggleの勉強を始めてみてください。
また、このコンペを通して課題が見つかったので解決していきます。

#付録（Appendix）
GridSearchCV

#GridSearchCVをimport
from sklearn.model_selection import GridSearchCV

#trainデータと検証データに分割
X_train, X_val, Y_train, Y_val = train_test_split(x_train, y_train, test_size = 0.3, random_state = 123)

# パラメータの候補
params = {"colsample_bytree": [0.5,1.0],
        "learning_rate":[0.1,0.3,0.5],
        "max_depth": [2,3,5,10],
        "subsample":[0.5,0.8,0.9,1],
         }
# モデルにインスタンス生成
mod = xgb.XGBClassifier(max_depth = 6, 
                        learning_rate = 0.3, 
                        n_estimators=100, 
                        objective='reg:squarederror', 
                        gamma=0, 
                        min_child_weight=1, 
                        subsample=1, 
                        colsample_bytree=1)

kf = KFold(n_splits=5, shuffle=True)

# ハイパーパラメータ探索準備（モデル）
#refit = True（デフォルト）：best_estimator_を返す
cv = GridSearchCV(mod, params, cv = kf, scoring= "accuracy", n_jobs =-1)

# ハイパーパラメータ探索
evallist = [(x_train, y_train)]
cv.fit(X_train, Y_train, eval_metric='rmse', eval_set=evallist, early_stopping_rounds=10)

#予測    
y_train_pred = cv.predict(X_train)
y_test_pred = cv.predict(X_val)
print()
print("グリッドサーチcv検証データScore：{}".format(accuracy_score(y_test_pred, Y_val)))

• 正解率：86%
• Kaggle_Score（提出結果）:78%

GridSearchCVの学習後、最も精度が高くなったハイパーパラメータは以下のコードで確認できます。

#最もスコアが高くなったハイパーパラメータを表示
print(cv.best_params_)

＜ハイパーパラメータの意味＞

・colsample_bytree：決定木ごとに特徴量をサンプリングする割合(0~1)

・learnig_rate：学習率(0~1)

・max_depth：決定木の深さ

・subsample：決定木ごとに学習データをサンプリングする割合(0~1)

＜変更点＞

GridSearchCVでの学習結果は、過学習していたので、
Learnig_rateの値を0.3→0.1に減少させ、過学習を抑制しました。
subsampleの値を0.5→0.9に増加させ、学習データに対するサンプリングの割合を増加させ、データに対する過剰適合を抑制しました。