混合ガウス分布問題のEMアルゴリズム計算

こんにちは。
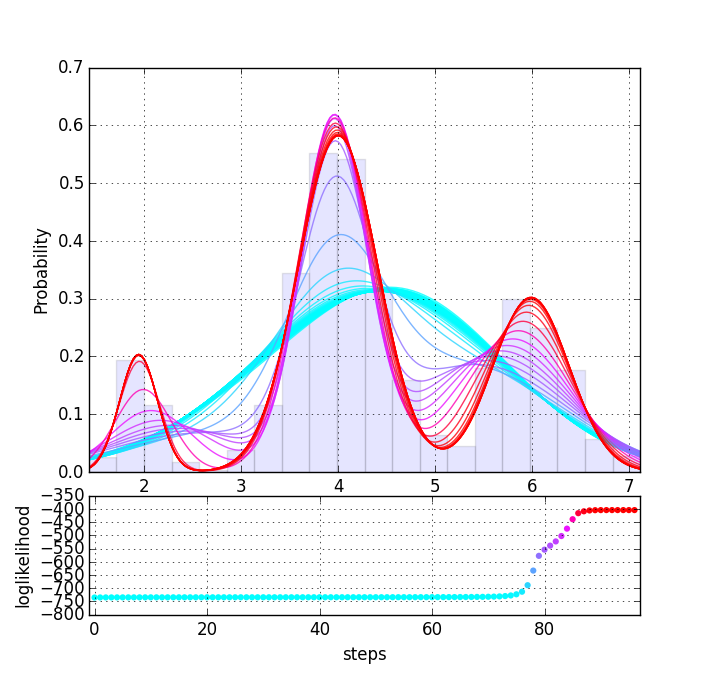
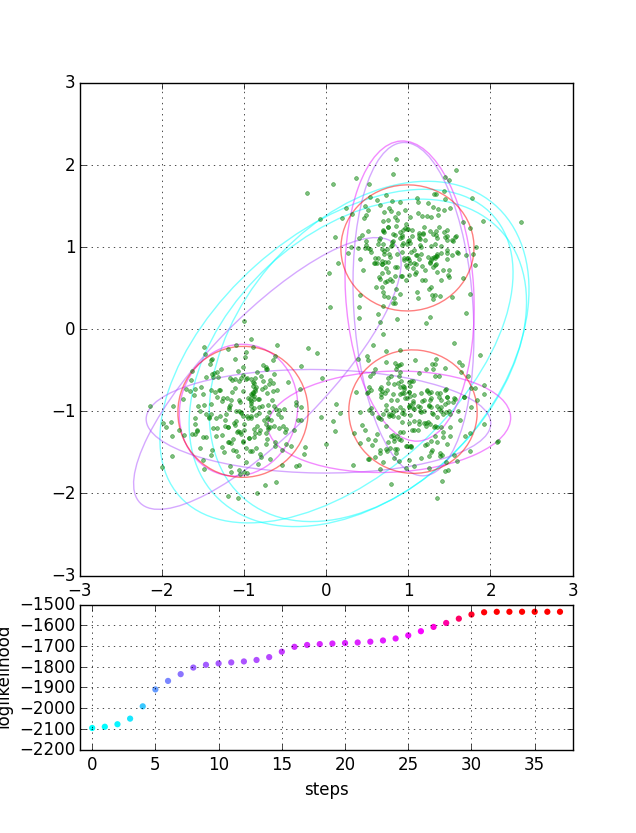
混合ガウス分布問題のEMアルゴリズム計算をPythonで書きました。１変量と２変量の例です。初期値等をランダム生成しているので繰り返し走らせると収束の進行はいろいろ変わることが分かります。

$ ./em.py --univariate
nstep= 98  log(likelihood) = -404.36

$ ./em.py --bivariate
nstep= 39  log(likelihood) = -1534.51

em.py

#!/usr/bin/env python
# -*- coding: utf-8 -*-

from __future__ import division
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
from matplotlib.patches import Ellipse

#混合ガウス分布  par = (pi, mean, var): (混合係数、平均、分散)
def gaussians(x, par):
    return [gaussian(x-mu, var) * pi for pi,mu,var in zip(*par)]

#ガウス分布
def gaussian(x, var):
    nvar = n_variate(x)
    if not nvar:
        qf, detvar, nvar = x**2/var, var, 1
    else:
        qf, detvar = np.dot(np.linalg.solve(var, x), x), np.linalg.det(var)
    return np.exp(-qf/2) / np.sqrt(detvar*(2*np.pi)**nvar)

#対数尤度
def loglikelihood(data, par):
    gam = [gaussians(x, par) for x in data]
    ll = sum([np.log(sum(g)) for g in gam])
    return ll, gam

#Eステップ
def e_step(data, pars):
    ll, gam = loglikelihood(data, pars)
    gammas = transpose(map(normalize, gam))
    return gammas, ll

#Mステップ  pars = (pis, means, vars)
def m_step(data, gammas):
    ws = map(sum, gammas)
    pis = normalize(ws)
    means = [np.dot(g, data)/w for g, w in zip(gammas, ws)]
    vars = [make_var(g, data, mu)/w for g, w, mu in zip(gammas, ws, means)]
    return pis, means, vars

#共分散
def make_var(gammas, data, mean):
    return np.sum([g * make_cov(x-mean) for g, x in zip(gammas, data)], axis=0)

def make_cov(x):
    nvar = n_variate(x)
    if not nvar:
        return x**2
    m = np.matrix(x)
    return m.reshape(nvar, 1) * m.reshape(1, nvar)

#n-変量
def n_variate(x):
    if isinstance(x, (list, np.ndarray)):
        return len(x)
    return 0  # univariate

#正規化
def normalize(lst):
    s = sum(lst)
    return [x/s for x in lst]

#転置
def transpose(a):
    return zip(*a)

def flatten(lst):
    if isinstance(lst[0], np.ndarray):
        lst = map(list, lst)
    return sum(lst, [])

# 楕円
def ellipse(cov, mstd=1.0):
    vals, vecs = eigsorted(cov)
    radii = mstd * np.sqrt(vals)
    tilt = np.degrees(np.arctan2(*vecs[:,0][::-1]))
    return radii, tilt

def eigsorted(cov):
    vals, vecs = np.linalg.eigh(cov)
    order = vals.argsort()[::-1]
    return vals[order], vecs[:,order]

# color map
def cm(x, a=0.85):
    if x > a:
        return (1, 0, (1-x)/(1-a), 1)
    return (x/a, 1-x/a, 1, 1)

#結果のプロット
def plot_em(data, ls, par):
    nvar = n_variate(data[0])
    col = [cm((l-ls[0])/(ls[-1]-ls[0])) for l in ls]
    ax1 = plt.subplot2grid((4, 1), (0, 0), rowspan=3)  # subplot(211)
    ax2 = plt.subplot2grid((4, 1), (3, 0))  # subplot(212)
    if not nvar:
        subplot_hist(data, par, col, ax1)
    elif nvar == 2:
        subplot_bivariate(data, ls, par, col, ax1)
    subplot_loglikelihood(ls, col, ax2)
    plt.show()
    return 0

#ヒストグラムの表示（単変量）
def subplot_hist(data, pars, col, ax):
    xs = np.linspace(min(data), max(data), 200)
    ax.hist(data, bins=20, normed=True, alpha=0.1)
    for par, c in zip(pars, col):
        norm = [mlab.normpdf(xs, m, np.sqrt(var))*pi for pi,m,var in zip(*par)]
        ax.plot(xs, sum(norm), c=c, lw=1, alpha=0.8)
    ax.set_xlim(min(data), max(data))
    ax.set_xlabel("x")
    ax.set_ylabel("Probability")
    ax.grid()
    return 0

# 2変量ガウス分布の表示
def subplot_bivariate(data, ls, par, cols, ax):
    x, y = zip(*data)
    ax.plot(x, y, 'g.', alpha=0.5)
    ax.grid()
    ax.set(aspect=1) # 'equal'
    nstep = 4
    mstd = 4.0
    for i in range(nstep):
        j = ((len(ls)-1)*i)//(nstep-1)
        (pi, mean, cov), col = par[j], cols[j]
        for m, c in zip(mean, cov):
            radii, tilt = ellipse(c, mstd)
            ax.add_artist(Ellipse(xy=m, width=radii[0], height=radii[1], angle=tilt, ec=col, fc='none', alpha=0.5))
    return 0

#対数尤度の推移
def subplot_loglikelihood(ls, col, ax):
    ax.scatter(range(len(ls)), ls, c=col, edgecolor='none')
    ax.set_xlim(-1, len(ls))
    ax.set_xlabel("steps")
    ax.set_ylabel("loglikelihood")
    ax.grid()
    return 0

#混合ガウス分布データ（K: 混合ガウス分布の数）
def make_data(typ_nvariate):
    if typ_nvariate == 'univariate':  # 単変量
        par = [(2.0, 0.2, 100), (4.0, 0.4, 600), (6.0, 0.4, 300)]
        data = flatten([np.random.normal(mu,sig,n) for mu,sig,n in par])
        K = len(par)
        means = [np.random.choice(data) for _ in range(K)]
        vars = [np.var(data)]*K
    elif typ_nvariate == 'bivariate':  # 2変量
        nvar, ndat, sig = 2, 250, 0.4
        centers = [[1, 1], [-1, -1], [1, -1]]
        K = len(centers)
        data = flatten([np.random.randn(ndat,nvar)*sig + np.array(c) for c in centers])
        means = np.random.rand(K, nvar)
        vars = [np.identity(nvar)]*K
    pis = [1.0/K]*K
    return data, (pis, means, vars)

#EMアルゴリズム（gammas: 'burden rates', or 'responsibilities'）
def em(typ_nvariate='univariate'):
    delta_ls, max_step = 1e-5, 400
    lls, pars = [], []  #各ステップの計算結果を保存
    data, par = make_data(typ_nvariate)
    for _ in range(max_step):
        gammas, ll = e_step(data, par)
        par = m_step(data, gammas)
        pars.append(par)
        lls.append(ll)
        if len(lls) > 8 and lls[-1] - lls[-2] < delta_ls:
            break
    # 結果出力
    print('nstep=%3d' % len(lls), " log(likelihood) =", lls[-1])
    plot_em(data, lls[1:], pars[1:])
    return 0

def main():
    """{f}: EM algorithm for a Gaussian mixture problem.

    usage: {f} [-h] [--univariate | --bivariate]

    options:
        -h, --help    show this help message and exit
        --univariate  calculates a univariate problem (default)
        --bivariate   calculates a bivariate problem
    """
    import docopt, textwrap
    args = docopt.docopt(textwrap.dedent(main.__doc__.format(f=__file__)))
    typ_nvariate = ["univariate", "bivariate"][args["--bivariate"]]
    em(typ_nvariate)

if __name__ == '__main__':
    main()