More than 3 years have passed since last update.

点と多角形の辺との最短距離

Last updated at 2021-12-21Posted at 2016-04-10

こんにちは。
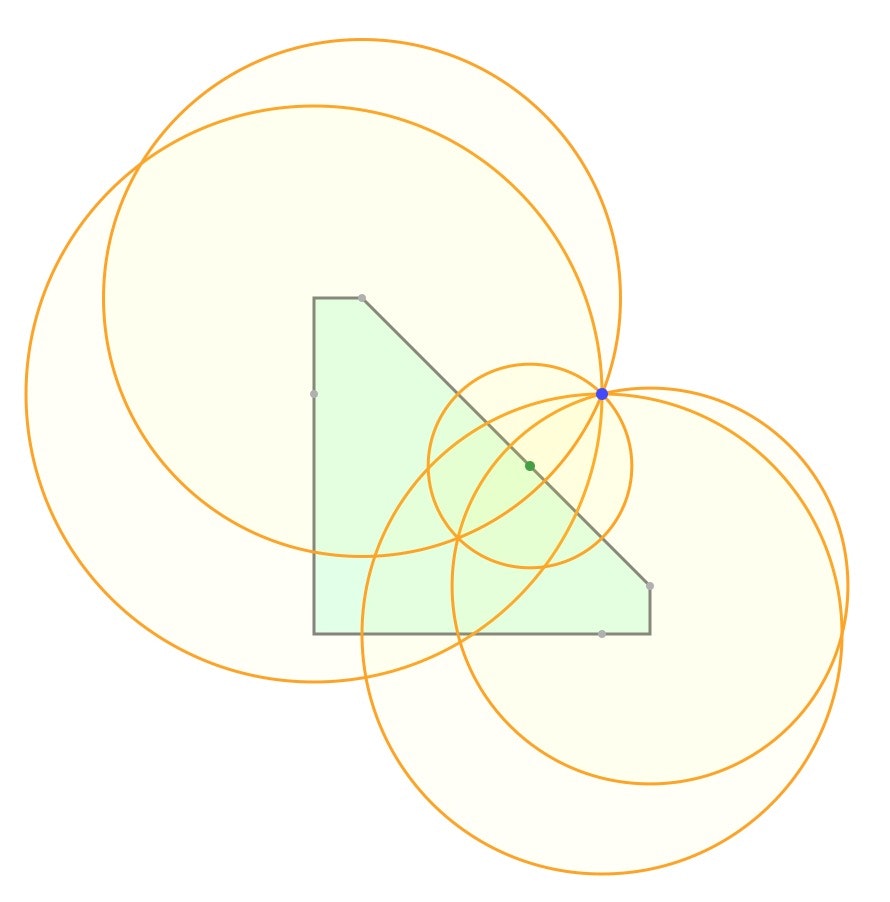
与えられた点と多角形（polygon）の辺（線分 line segment）との最短距離を求めてみました¹。

各辺上の最短距離点を求め、その点・距離を中心・半径とする円を描いており、各円周線は与えられた点を通ります。最近傍辺が最小半径円に対応します。

pointToPolygon.html

<!DOCTYPE html>
<html>
<head>
<meta charset="utf-8">
<title></title>
<script src="http://d3js.org/d3.v3.min.js"></script>
</head>
<body>
<div id="canvas"></div>
<script type="text/javascript">

function dotTo(a, b, dest) {
  for (var z=0, i=a.length-1; i>=0; i--) {
    z += (a[i]-dest[i])*(b[i]-dest[i])
  }
  return z;
}

function distanceSquared(a, b) {
  return dotTo(a, a, b);
}

function linearCombination(a, b, s, t) {
  for (var c=[], i=0, len=a.length; i<len; i++) {
    c.push(a[i]*s+b[i]*t);
  }
  return c;
}

function pointToPolyline(point, poly) {
  for (var i=0, z=[], len=poly.length, j=len-1; i<len; j=i++) {
    z.push(pointToLineSegment(point, poly[i], poly[j]));
  }
  return z;
}

// pointToLineSegment
//   inputs: point, pointStart_LineSegment, pointEnd_LineSegment
//   output: [foot.x, foot.y, distance**2]
function pointToLineSegment(point, pointStart, pointEnd) {
  var foot, dotToStart = dotTo(point, pointEnd, pointStart);
  if (dotToStart<=0) {
    foot = pointStart;
  } else {
    var dotToEnd = dotTo(point, pointStart, pointEnd);
    if (dotToEnd<=0) {
      foot = pointEnd;
    } else {
      var t = dotToStart/(dotToStart+dotToEnd);
      foot = linearCombination(pointStart, pointEnd, 1-t, t);
    }
  }
  return foot.concat(distanceSquared(point, foot));
}

function indexOfApply(func, arr) {
    return arr.indexOf(func.apply(null,arr));
}

function mytransform(p) {
    var scale = 24, offset = 160;
    q = [p[0]*scale+offset, (7-p[1])*scale+offset];
    if (p.length>2) {q.push(p[2]*scale)} 
    return q;
}

var point = [6,5], poly = [[0,0], [7,0], [7,1], [1,7], [0,7]];
var circles = pointToPolyline(point, poly).map(function(p){return [p[0], p[1], Math.sqrt(p[2])]});
var imin = indexOfApply(Math.min, circles.map(function(p){return p[2]}));
point = mytransform(point);
poly = poly.map(mytransform);
circles = circles.map(mytransform);

var svg = d3.select("#canvas")
    .append("svg")
    .attr("width",450)
    .attr("height",450);

svg.append("polygon")
    .data([poly])
    .attr("points", function(d){return d.join(" ")})
    .attr("stroke", "gray")
    .attr("fill", "#e0fff0")
    .attr("stroke-width", 1.5);

svg.selectAll('circle').data(circles).enter().append('circle').attr({
      'cx': function(d) {return d[0];},
      'cy': function(d) {return d[1];},
      'r': function(d) {return d[2];}
    }).attr("stroke", "orange").attr("stroke-width", "1.5").attr("fill","yellow").attr("fill-opacity", 0.04);

svg.selectAll("points")
    .data([point])
    .enter().append("circle")
    .attr("fill", "#4040ff")
    .attr("r", 3)
    .attr("transform", function(d){return `translate(${d})`});

svg.selectAll("points")
    .data(circles.map(function(d){return d.slice(0,2)}))
    .enter().append("circle")
    .attr("fill", "#b0b0b0")
    .attr("r", 2)
    .attr("transform", function(d){return `translate(${d})`});

// the minimum distance point on a polygon
svg.selectAll("points")
    .data([circles[imin].slice(0,2)])
    .enter().append("circle")
    .attr("fill", "#40a040")
    .attr("r", 2.5)
    .attr("transform", function(d){return `translate(${d})`});

</script>
</body>
</html>

ref: "Distance from a point to a line" (Wikipedia)） ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up