基本的にこの記事は機械学習初心者の私自身のためにメモ感覚で書いたものです。多く雑な所が見られます、すみません。事細かくつくつもりではなく、あくまでgeneral ideaが掴めることが目標です。
SVDとは
この動画を見るとわかりやすい(https://www.youtube.com/watch?v=P5mlg91as1c)
SVDはData Dimensionality Reduction技法のうちの一つだ。以下はDefinitionと詳細。

3行列のproductがSVD。
Aはm*nの行列。文書行列で例えるとrowが文書、columnが単語で各文書に各単語が出現したかしてないかを0か1のvalueで表す。または、movie、user行列で例えるとrowがmovie、columnがuserで、そのuserがあるmovieを見たか見てないか0,1で表す。
Σはr*rの対角行列(対角線上以外は0)。前提として値はdescending order(一番大きいのが最初、二番目が次。。。).
UとVは左or右のベクトル。rは行列Aのランクの意。
次はGraphicalに捉えてみよう。以下詳細。

input Aを頂く。見ての通り,mrの行列、対角行列、nrのTranspose行列を掛け合わせる。つまり下の画像の意だよねってこと。

次に、property.

AをSVDに変換する際、3つの行列はinput Aに対してたった1つずつしか存在しない。
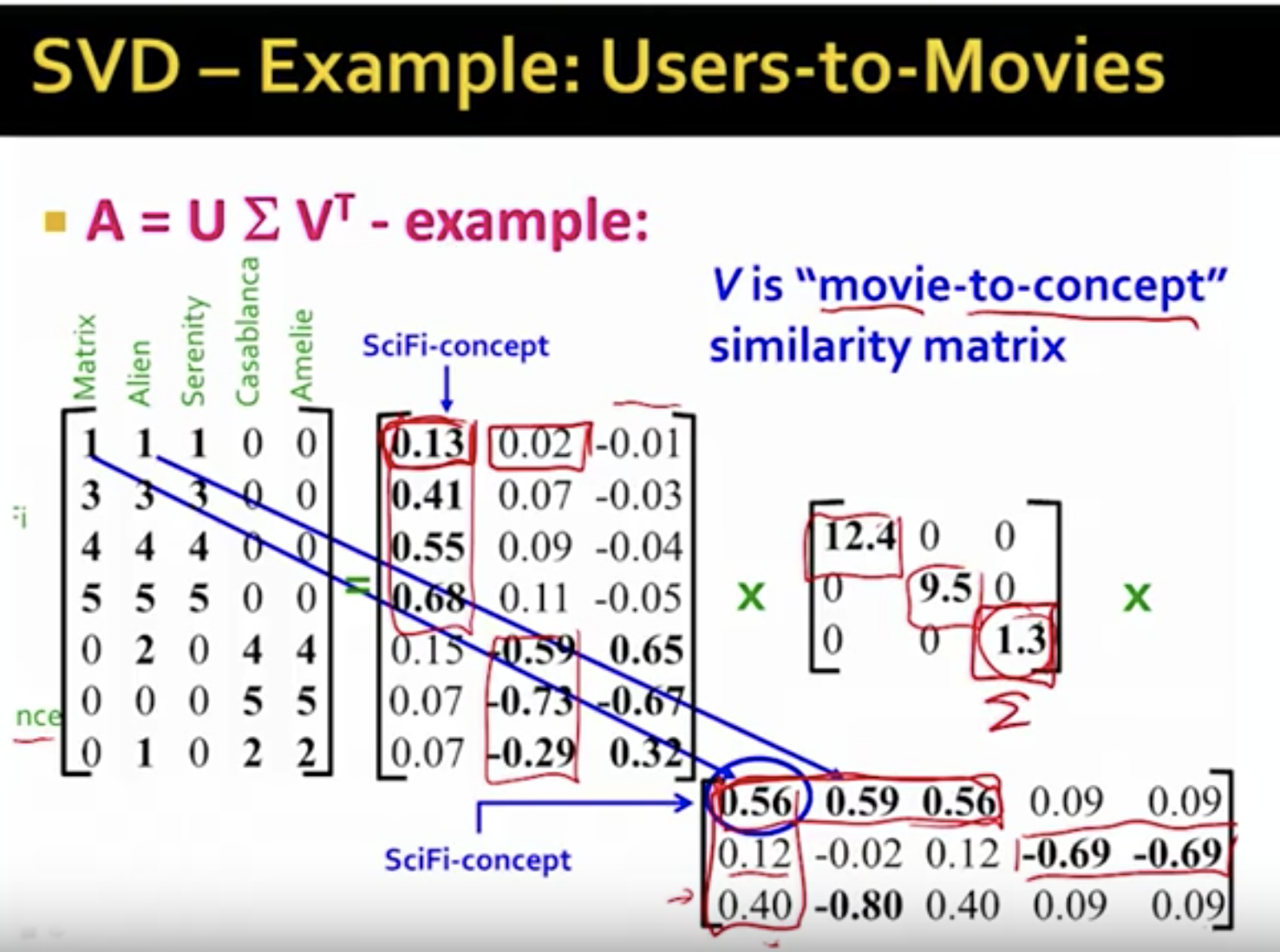
A is the user * movie matrix. The value is from 0 to 5, which indicate how much you like(5) or dislike(0) each movie. A can be divided, the scifi movies, romance-movies, third one is others which can be ignored.
U is user-to-concept matrix. First column is SciFi-concept. As you can see, first 4 user shows favorableness to scifi-concept, so the values are high. So as romance-movie is.
Sigma shows strength of each concept. This means scifi-concept is important in this matrix, but third one is the least important in this matrix.
V shows movie-to-concept matrix. This shows how much each movie corresponds to each concept.
以上がSVDのgeneral idea. つまり行列Aの特徴を抽出して、各特徴のStrength(重要度?)に基づきdata matrixをapproximateしちゃおうって感じなのかな。あとPCA(主成分分析)と考え方(各featureの代表的特徴を抽出しようという点)が似ているのかな。How it works in detail? What does the rank mean?とか細かい疑問は多々あるが、目的は果たせたので次回のお楽しみ。