ロトカ-ヴォルテラ方程式
うーん、この中学二年生が考えたような名前の方程式。
超絶かっこいい。
今回はこの方程式を数値計算(python)で遊んでみたいと思います。
方程式の中身自体はこんな感じになっています。
\frac{dx}{dt}=\alpha x-\beta xy \\
\frac{dy}{dt}=\gamma x-\delta xy
まあまあいかつい数式ですが、この方程式は捕食と被捕食の関係を表した数式です。見掛け倒しで実はそんなに難しくないので安心してください!!今回はライオンvsガゼルというアフリカ設定で読み解いていきます。
式の理解
たくさんの文字が出てきていますが、一つずつ説明します。
変数・定数の定義
変数
$x$ : 被捕食側の数(ガゼルの数), $y$ : 捕食側の数(ライオンの数)
定数
$\alpha$ : 被捕食側の出生率, $\beta$ : 被捕食率, $\gamma$ : 捕食側の出生率, $\delta$ : 捕食側の死亡率
(学術的には正確では部分もありますが分かりやすさを重視しています)
脳内が???となってる方もいると思いますが、次の節で説明するので少しお待ちください。
式への意味付け
さあここが一番面白いところですよ!!上で定義した文字の意味を見ながら、もとの数式を眺めてみましょう。
\frac{dx}{dt}=\alpha x-\beta xy~~~~(1) \\
\frac{dy}{dt}=\gamma xy-\delta y~~~~(2)
まずは(1)について考えてみましょう。
\frac{dx}{dt}=\alpha x-\beta xy~~~~(1)
左辺は$x$の時間変化率、つまりガゼルがどれだけ増えるかを意味しています。じゃあガゼルの増減として考えられるのは何でしょうか。そう、出産と死亡ですよね。出産が第一項の $\alpha x$ , 死亡が $\beta xy$ に相当します。
ガゼルの出産、つまりガゼルの生まれる数はガゼルの数と出生率の積($=\alpha x$)で表せます(ガゼル全体が100匹で出生率が0.1なら10匹ガゼルは増える)。
一方で、ガゼルの死亡、ガゼルが減る数はガゼルの数とライオンの数と被捕食率の積(=$\beta xy$) で表せます。ここが少し分かりづらいかと思いますが、ガゼルが多ければライオンに狙われやすくなり、ライオンが多ければガゼルが沢山捕食されてしまうことをイメージしてもらうと分かりやすくなるかと思います。
したがって、ガゼルの増減のトータルは生まれた数と死亡した数を合わせて $\alpha x-\beta xy$ となります。
同じことを(2)の式でも考えてみましょう。
\frac{dy}{dt}=\gamma xy-\delta y~~~~(2)
左辺は$y$の時間変化率なのでライオンがどれだけ増えるかに相当します。ライオンの増減もまた出産と死亡に分けて考えられますが、少しガゼルとは異なる要素があります。
ライオンの生まれる数はライオンの数とガゼルの数と出生率の積 ($=\gamma xy$) で表されます。何でガゼルの数が関係あるの??と思った読者の方は鋭いです。もし自分がライオンだったとしたら、獲物のガゼルが大量にいればいるほど子孫繁栄させられると感じませんか?そういうテンションです。
さて、ライオンの死亡数はライオンの数と死亡率の積 ($=\delta y$) で表されます。ライオンはガゼルから食べられるようなことはないので、ガゼルの数とは関係なく死亡数が決まります。
したがって、ライオンの増減のトータルは生まれた数と死亡した数を合わせて $\gamma xy-\delta y$ となります。
数値計算してみる
前節でガゼルとライオンについての理解を深めて式が理解できたかと思います。ただ、微分方程式は計算機で直接扱うことができないので、今回は差分法を用いて計算を行います。
時刻$n$における$x, y$を$x_{n}, y_{n}$と表すとします。
これが
\frac{dx}{dt}=\alpha x-\beta xy~~~~(1) \\
\frac{dy}{dt}=\gamma xy-\delta y~~~~(2)
差分化するとこうなって、
\frac{x_{n+1}-x_{n}}{\Delta t}=\alpha x_{n}-\beta x_{n}y_{n}~~~~(1) \\
\frac{y_{n+1}-y_{n}}{\Delta t}=\gamma x_{n}y_{n}-\delta y_{n}~~~~(2)
次の時刻$n+1$における未知の値$x_{n+1}, y_{n+1}$について解くと、
x_{n+1}=(\alpha -\beta y_{n})x_{n}\Delta t + x_{n}~~~~(1) \\
y_{n+1}=(\gamma x_{n} -\delta)y_{n}\Delta t + x_{n}~~~~(2)
になります。右辺の値は既知の値(定数or時刻nの値)で成り立っているので、ただ代入計算をするだけで左辺が求まります。
ソースコード
今回はpythonで書きました。定数の値は好きに変えることができます。
import numpy as np
import matplotlib.pyplot as plt
# 係数
a, b, c, d = 0.3, 0.1, 0.3, 1.3
# 初期値
init_x = 10
init_y = 2
# 時間進行
dt = 0.01
n = 5000
# 配列の初期化
x = np.zeros(n)
x[0] = init_x
y = np.zeros(n)
y[0] = init_y
for i in range(1, n):
x[i] = (a - b * y[i - 1]) * x[i - 1] * dt + x[i - 1]
y[i] = (c * x[i - 1] - d) * y[i - 1] * dt + y[i - 1]
print(i, x[i], y[i])
t = np.arange(0, n * dt, dt)
plt.plot(t, x, label="Prey")
plt.plot(t, y, label="Predator")
plt.legend()
plt.show()
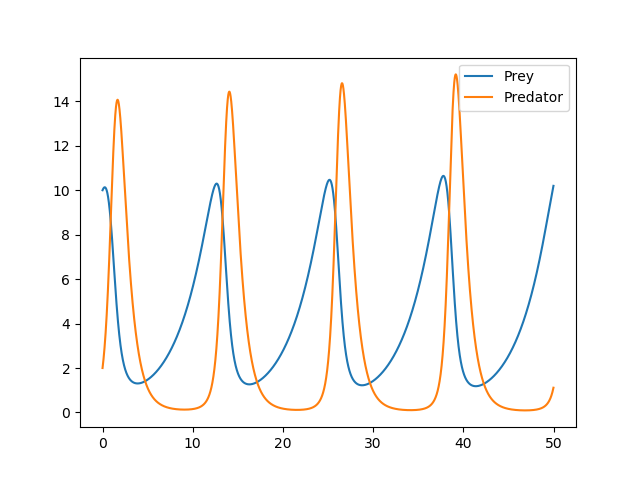
結果
考察
結果が振動するのが面白いですね。時系列を追って考察していくと、
- ライオン(黄)が増えてガゼル(青)が減っていく
- ライオンの増加が止まって減少し始め、それに伴ってガゼルが増える
- ガゼルが増加していくがしばらくするとライオンが増えてきてガゼルが減る
- これの繰り返し
になっています。
1. ライオン(黄)が増えてガゼル(青)が減っていく
まあその通りですね。ライオンが増えたらそりゃガゼルが食べられまくって減っていきます。
2. ライオンの増加が止まって減少し始め、それに伴ってガゼルが増える
ライオンが増えすぎた結果、餌が足りなくなって飢死し始めます(何か暗示のようなものを感じますね...)。そしてライオンが減った結果としてガゼルがここぞとばかりに勢いを取り戻して増加し始めます。
3. ガゼルが増加していくがしばらくするとライオンが増えてきてガゼルが減る
ガゼルが増えるとライオンさんにとっては天国になります。そしてガゼルが減っていきます
4. これの繰り返し
そうです、この世界はこのサイクルで永遠と回っていきます。何か不思議な気分になりますね。
まとめ
今回はロトカ-ヴォルテラ方程式という名前だけでもうかっこいい方程式を使って、ライオンとガゼルの生態系について数値計算をしてみました。面白いと感じた方がいれば嬉しいです!よければいいねお願いします!!