なぜ人は素数を追い求めるのか
2018年12月7日、GIMPSによって最大の素数が更新されました。
発見された素数は $2^{82589933} - 1 $ 、2400万桁を超える巨大な数です。
そんなに計算したところで何の意味が...と思われるかもしれませんが、実は巨大な素数は国家機密として扱われている(らしいです)。
なぜなら、素数はRSA暗号の鍵として使われているからです。RSA暗号は桁数が大きな合成数の素因数分解が困難であるという前提のもと、成り立っている暗号です。
簡単に説明すると、2つの大きな素数が暗号化・復号化の鍵になり、暗号化が行われます。暗号を解読するには数百桁の合成数を素因数分解する必要があり、現在のコンピュータでは有限時間で解読不可能であるため、今のところ安全とされています。
つまり、素数の大きさがそのまま暗号の強さに相当するため、巨大な素数をどんどん見つけて、より強固な鍵を手に入れようということです。
(最近では楕円曲線暗号(ECC)に主流が移りつつあります)
では、巨大な素数をどのようにして見つけるのか。
Goを使って大きな素数と戯れながら、実際の素数判定アルゴリズムがどの程度のパフォーマンスなのか検証します。
素数判定アルゴリズム
素数判定アルゴリズムは様々なところで紹介されていますので、さらっといきます。
一般的に素数判定法は決定的な判定法と確率的な判定法に分類され、前者は素数であるかどうかを確実に判定し、後者はある確率で合成数を素数と判定してしまう方法です。決定的素数判定法は計算量が多くなりがちで、確率的素数判定法は計算量が少なくなる傾向にあります。
今回はエラトステネスの篩、リュカーレーマーテスト、ミラー-ラビンテストについて実装ベースで見ていきます。
**アルゴリズムをより詳しく見たい方はこちらをどうぞ**
決定的素数判定法
判定したい数を $n$ する
愚直な方法
- 素数の定義で求める
- プログラミング入門書で頻出
- 当然ながら最も非効率 $O(\sqrt{n})$
- アルゴリズム
- $n$ を $\sqrt{n}$ 以下の奇数 $k$ で割っていく
- 全ての奇数 $k$ で割り切れなければ $n$ は素数
エラトステネスの篩
- $n$ までの素数をすべて発見するための手法
- 単純な方法だが、小さい素数を見つける方法としてはかなり高速 $O(N \log \log N)$
- 求める素数以下の数が必要になるので、数が大きくなるとメモリが足りなくなる
- アルゴリズム
- $n$ までの整数を用意し、すべての数に素数フラグを立てる
- $k = 2$ として
- $k$ の倍数となる数の素数フラグを全て折る
- $k$ をインクリメントし、次に素数フラグが立っている数 = $k$ とする
- 3~4を繰り返し、$k$ が $n$ の平方根を超えたら終了。素数フラグが立っている数が素数
AKS素数判定法
- 決定的多項式時間で判定できる世界初のアルゴリズム
- 多項式時間について ―― $n^2$ や$n^{100}$ は多項式時間である一方、$2^n$ や $n^{\log n}$ は指数関数時間となり $n$ が大きくなるにつれて計算量は膨大になる
- 計算量は $\tilde{O}(\log(n)^{7.5})$
- ただし、 $f(x) = \tilde{O}(g(x)) \Leftrightarrow f(x) = O(g(x)) \cdot Poly(\log g(x)))$
- 多項式時間とはいえ次数が7.5と高いので、巨大な素数では太刀打ちできない
- 決定的アルゴリズムでは最速
- アルゴリズムの詳細はAKS素数判定法を参照
- 計算途中に無理数が出現するため、コンピュータで扱うのは不向きであり実際の計算量はオーダーより大きくなる
リュカ-レーマーテスト
- メルセンヌ数に対する素数判定法
- 世の最大素数がメルセンヌ素数ばかりなのは、このテストがあるため
- アルゴリズムはリュカ-レーマーテストを参照
確率的素数判定法
確率的素数判定法の場合、判定結果が真であった場合に、その数が真に素数である確率が重要となる
フェルマーテスト
-
フェルマーの小定理の待遇を用いた判定法
- $a^{n-1} \not \equiv 1 ( \mod n )$ なら素数
-
RSA暗号にも応用されている手法
-
$1/2$ 以上の確率で素数
- ただし、カーマイケル数といわれる数は必ず素数と判定されてしまう
-
アルゴリズム
2. 2以上 $n$ 未満の自然数 $a$ を決める
3. $a$ と $n$ が互いに素でなければ、$n$ は合成数
4. $a^{n-1} \not \equiv 1 ( \mod n )$ ならば $n$ は合成数、そうでなければ $n$ は素数
ミラー-ラビンテスト
- フェルマーテストの改善版
- $3/4$ 以上の確率で素数
- アルゴリズムはミラー-ラビン素数判定法を参照
Goで大きな数を扱うには
一般的なCPUは64bitですので、ハードウェアで扱える最大数は $2^{64}$ までとなります。16~7桁程度ではお話になりません。
そこで速度はグンと落ちますが、ソフトウェアで解決するしかありません。Goにはメモリが許す限りの桁数を扱える、math/bigパッケージがあります。基本的な四則演算やべき乗、小数点以下の数値や分数も扱える万能パッケージです。
普段使っている演算子は使えないので、若干使いづらいところもあります。とはいえ、無限桁を扱うにはこのパッケージを使わない手はないでしょう。
math/big をエラトステネスの篩で検証する
ハードウェアとソフトウェアで性能差がありますが、実際どの程度の差が生まれるのか見てみます。
具体的にはint64型とbig.Int型でどれだけ実行時間が変化するのか検証します。
int64のコードですが、比較のためにあえて構造体を用意しています。両者のコードが極力同じになるよう記述しました。
int64
https://github.com/kiyocy24/prime-benchmark/blob/master/eratosthenes/eratosthenes.go
package eratosthenes
import "math"
type Number struct {
value int64
isPrime bool
}
func Genarate(max int64) []int64 {
numbers := make([]*Number, max)
for n := int64(0); n < max; n++ {
num := &Number{
value: n,
isPrime: true,
}
numbers[n] = num
}
limit := int64(math.Sqrt(float64(max)))
for _, num := range numbers {
if num.value < 2 || limit < num.value {
continue
}
idx := int64(num.value * 2)
if num.isPrime {
for i := int64(2); idx < int64(len(numbers)); i++ {
numbers[idx].isPrime = false
idx = int64(num.value) * i
}
}
}
var primes []int64
for _, num := range numbers {
if num.value < 2 {
continue
}
if num.isPrime {
primes = append(primes, num.value)
}
}
return primes
}
big.Int
https://github.com/kiyocy24/prime-benchmark/blob/master/eratosthenes/eratosthenes_big.go
package eratosthenes
import (
"math"
"math/big"
)
type NumberBig struct {
value *big.Int
isPrime bool
}
func GenarateBig(max int64) []*big.Int {
numberBigs := make([]*NumberBig, max)
for n := int64(0); n < max; n++ {
ng := &NumberBig{
value: big.NewInt(n),
isPrime: true,
}
numberBigs[n] = ng
}
two := big.NewInt(2)
limit := big.NewInt(int64(math.Sqrt(float64(max + 1))))
for _, ng := range numberBigs {
if ng.value.Cmp(two) == -1 || ng.value.Cmp(limit) == 1 {
continue
}
if ng.isPrime {
idx := int64(ng.value.Int64() * 2)
for i := int64(2); idx < int64(len(numberBigs)); i++ {
numberBigs[idx].isPrime = false
idx = ng.value.Int64() * i
}
}
}
var primes []*big.Int
for _, ng := range numberBigs {
if ng.value.Cmp(two) == -1 {
continue
}
if ng.isPrime {
primes = append(primes, ng.value)
}
}
return primes
}
ベンチマーク結果
テストコード
-
https://github.com/kiyocy24/prime-benchmark/blob/master/eratosthenes/eratosthenes_test.go
-
https://github.com/kiyocy24/prime-benchmark/blob/master/eratosthenes/eratosthenes_big_test.go
実行環境はGCP e2-standard-4(vCPU x 4、メモリ 16 GB)です。
$ go test -bench . -benchmem -benchtime 1m
goos: linux
goarch: amd64
pkg: github.com/kiyocy24/prime-benchmark/eratosthenes
BenchmarkGenerateBig5-4 58 20385714 ns/op 6789153 B/op 300022 allocs/op
BenchmarkGenerateBig6-4 337 220395485 ns/op 67691290 B/op 3000031 allocs/op
BenchmarkGenerateBig7-4 27 2329945300 ns/op 668823846 B/op 30000040 allocs/op
BenchmarkGenerateBig8-4 3 28674377990 ns/op 6670908706 B/op 300000050 allocs/op
BenchmarkGenerate6-4 1136 70526622 ns/op 27691267 B/op 1000030 allocs/op
BenchmarkGenerate7-4 66 1005478486 ns/op 268823808 B/op 10000039 allocs/op
BenchmarkGenerate8-4 7 9431136358 ns/op 2670908672 B/op 100000049 allocs/op
PASS
ok
各ベンチマークの番号は10の何乗かを示しており、BenchmarkGenerateBig6であれば、big.Intを用いた $10^6$ までの数を篩にかけたことになります。
エラトステネスの篩にランダム性はないため、使用容量とアロケート量は何度やっても変化がありません。
メモリに関しては、桁数に応じて線形で扱うメモリが増加しています。Int64とbig.Intとの差は3倍強です。
時間についてもう少し整理すると、
| 10^5 | 10^6 | 10^7 | 10^8 | |
|---|---|---|---|---|
| Int64 | 0.0055 | 0.07 | 1.01 | 9.43 |
| big.Int | 0.02 | 0.22 | 2.33 | 28.67 |
10倍ぐらいの差が見られるのかなと思いましたが、最大でも3倍程度の差しか見られませんでした。おそらく、big.Intの内部でint型を使っていて、int型で対応できる計算に関しては大きな差が生まれないのだと思います。
ちなみに、int64型でNumber構造体を用意せず、最適化した場合でさらに3倍程度の高速化が実現できました。Goは速いといっても、使う人次第ということです。
ProbablyPrime を試す
big.Int 構造体には ProbabryPrime という関数が備わっています。Probably とあるように、確率的素数判定法であるミラー-ラビンテストとリュカ-レーマーテストを複合した関数です。コメントも非常に丁寧なので、この記事をここまで読んでいれば十分理解できると思います。
ミラー-ラビンテストで真と判定された数は 3/4以上 の確率で真に素数です。確率的素数判定法では内部で乱数が使われているので、何度も呼び出すことで判定精度を高めることができます。今回は試行回数を256回、つまり合成数を素数と誤認する確率は $(1/4)^{256} = 1 / 1024$ 以下です。
ミラー-ラビンテストでは判定結果にムラがあり、強擬素数と呼ばれる数はテストを通過してしまいます。そういったイレギュラーに対処するために、リュカ- レーマーテストをあわせて実行しているようです。では、公式が用意してくれた素数判定アルゴリズムがどれだけのパフォーマンスを発揮するか見てみましょう。
ベンチマーク結果
結果の見方
- AllX ... $10^X$ までの数全てを判定
- PrimeX ... X桁の素数を判定
- CompositeX ... X桁の合成数(素数 × 素数)を判定
go test -bench . -benchmem -timeout 24h
goos: linux
goarch: amd64
pkg: github.com/kiyocy24/prime-benchmark/prime
BenchmarkAll5-4 1 2988223658 ns/op 452523616 B/op 10190638 allocs/op
BenchmarkAll6-4 1 29358339008 ns/op 3850683528 B/op 83980931 allocs/op
BenchmarkAll7-4 1 312282873349 ns/op 33792369408 B/op 714594738 allocs/op
BenchmarkPrime16-4 1015 1188305 ns/op 44880 B/op 1051 allocs/op
BenchmarkPrime39-4 400 2957597 ns/op 333214 B/op 5421 allocs/op
BenchmarkPrime157-4 19 59161731 ns/op 886340 B/op 5432 allocs/op
BenchmarkPrime969-4 1 5126497789 ns/op 4400752 B/op 5449 allocs/op
BenchmarkPrime6987-4 1 1548131598162 ns/op 33620864 B/op 28976 allocs/op
BenchmarkPrime13395-4 1 10462139938329 ns/op 68121536 B/op 50646 allocs/op
BenchmarkComposite16-4 63542 18830 ns/op 5752 B/op 14 allocs/op
BenchmarkComposite83-4 15561 77254 ns/op 8169 B/op 29 allocs/op
BenchmarkComposite340-4 619 1953418 ns/op 179486 B/op 550 allocs/op
BenchmarkComposite1350-4 19 60747604 ns/op 2835463 B/op 2237 allocs/op
BenchmarkComposite12535-4 1 25345106461 ns/op 659126752 B/op 40959 allocs/op
PASS
ok github.com/kiyocy24/prime-benchmark/prime 12762.028s
全ての数を判定
エラトステネスの篩と比較してみます。(単位は秒)
| 10^5 | 10^6 | 10^7 | 10^8 | |
|---|---|---|---|---|
| エラトステネス(Int64) | 0.0055 | 0.07 | 1.01 | 9.43 |
| エラトステネス(big.Int) | 0.02 | 0.22 | 2.33 | 28.67 |
| ProbablyPrime | 2.99 | 29.36 | 312.28 | - |
大きな数に対してはかなり有効な手法なのですが、数千万程度の数であれば圧倒的にエラトステネスが速いです。ちなみに $10^8$ までの数に対してもテストしてみましたが、一向に終わる気配がないので測定を断念しました。
(記事を書いてから、愚直な方法も比較対象にあったほうが良かったなと思いました。後で追記しておきます。)
巨大な素数の判定
続いて巨大な素数の実行時間を比較します。大きな素数は簡単に見つからないので、桁数にばらつきがあるのはご容赦ください。
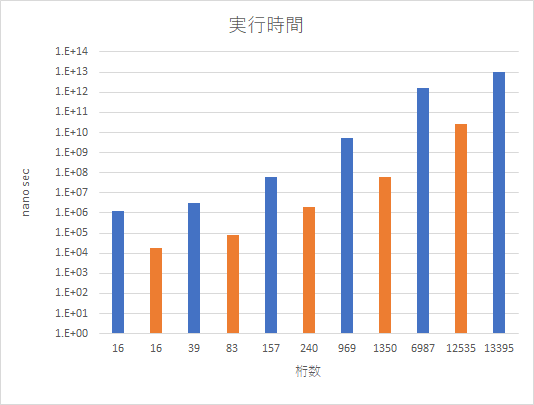
| Prime / Composite | 桁 | 実行時間 | 時間 / 桁 |
|---|---|---|---|
| Prime | 16 | 1.19 ms | 74.4 ns |
| Composite | 16 | 0.02 ms | 1.25 ns |
| Prime | 39 | 2.96 ms | 75.8 ns |
| Composite | 83 | 0.08 ms | 0.96 ns |
| Prime | 157 | 59.16 ms | 376 ns |
| Composite | 340 | 1.95 ms | 5.74 ns |
| Prime | 969 | 5.13 sec | 5.29 ms |
| Composite | 1350 | 0.06 sec | 45.0 ms |
| Prime | 6987 | 1564 sec | 221 sec |
| Composite | 12535 | 25.35 sec | 2021 ms |
| Prime | 13395 | 10462 sec (2.91 hour) | 781 sec |
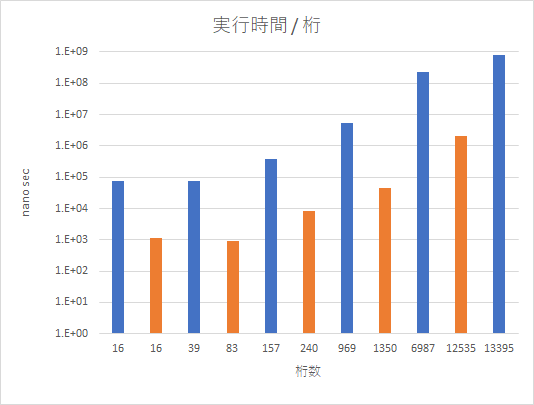
青が素数、橙が合成数です。対数グラフになっています。
まずは素数と合成数の実行時間の違いが目につきます。素数と合成数とで実行時間を比較すると合成数を反転する方が圧倒的に早いです。これは確率的素数判定法の長所であるのですが、1回目の試行で合成数と判定できた場合、以降の試行は不要なため劇的に計算量が減ります。また、合成数の中でも
一方、真に素数である場合、どこまでいっても合成数と判定されることはないので、試行回数の上限(今回であれば64回)の計算が必要になり、素数の判定にどうしても時間がかかってしまいます。12535桁の合成数と13395桁の素数の実行時間を比較すると、素数の場合では約400倍の差があります。大きな桁であればあるほど、精度を上げようとすればするほど、この差は顕著に現れます。
では、桁数と時間の関係を見てみると、対数グラフにも関わらず順調に右肩上がりになっています。桁数が上がるにつれて、桁当たりの実行時間が徐々に大きくなっているので、今後桁数が上がるにつれて必要時間は指数関数的に増えていくでしょう。テスト環境では3万桁程度で、10時間を超えてしまったので計測は断念しました。PCのスペックによりますが、実質的な素数判定の桁数は10万桁程度が限度かと思われます。
補足
冒頭にて、2400万桁の素数が見つかったと紹介しましたが、この計測結果からでは到底無理なのではと思われるかもしれません。発見した団体「GIMP」の正式名称は「Great Internet Mersenne Prime Search」つまり、メルセンヌ素数を見つけることを目的にしているので、リュカ-レーマーテストのみで事足りるわけです。それでも200万以上のCPUを使ってようやく見つけたわけですから、とんでもない計算が必要だったということです。
ちなみに、素数判定ではなく素因数分解の場合、さらに膨大な計算量が必要です。
まとめ
巨大な素数をGoで扱ってみました。
math/big パッケージは意外と計算速度が速かったなという印象です。内部で上手く最適化されているあたりはさすがGoといったところでしょうか。
数値型の上限を普段意識することは少ないですが、今回は巨大な素数ということでInt64型を超える値をがっつり使うことになりました。
業務で使うことは少ないかもしれませんが、数字遊びにはもってこいです。他にも非常に小さい数や分数も扱うことができます。
今度は円周率でも計算してみたいと思います。
最後に
DeNA では今年、以下の 3種 のアドベントカレンダーを書いてます!それぞれ違った種類なのでぜひ見てみてください。
- DeNA Advent Calendar 2020:DeNA エンジニアによるアドベントカレンダー
- DeNA 20 新卒 Advent Calendar 2020:DeNA 20 新卒エンジニアによるアドベントカレンダー
- DeNA 21 新卒 Advent Calendar 2021:DeNA 21 内定者エンジニアによるアドベントカレンダー"
この記事を読んで「面白かった」「学びがあった」と思っていただけた方、よろしければ Twitter や facebook、はてなブックマークにてコメントをお願いします!
また DeNA 公式 Twitter アカウント @DeNAxTech では、 Blog記事だけでなく色々な勉強会での登壇資料も発信してます。ぜひフォローして下さい!