1.はじめに
量子因数分解の方法としてショアのアルゴリズムが提案されている.参考文献1)ではN=21,m=5の場合の解法の手順が紹介されているが,QISkitによる実装は紹介されていない.本稿では,参考文献2)の手法を用いて,N=21,m=2などの場合についてQISkitで因数分解を行なえるプログラムを作成したので報告する.
2.問題設定
1)因数分解対象
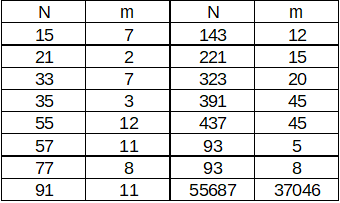
N=21,m=2などを入力.現在,下記は確認している.
表1 確認ずみ因数分解組合わせ
2)解析システム
RaspberryPi4+Python+QISkit
3.真理値表の作成
表2にN=21,m=2の場合の真理値表を示す.真理値表はExcelを用いて作成した.変数xの範囲は,y(1,2,4,8,16,11)が2周期以上現れるように,4ビットとした.実装したプログラムでは,自動的に真理値表を作成しているが,Nとmの組み合わせによっては位数rが大きくなりすぎて処理できない場合もあるので,事前に確認しておいた方が安全である.
表2 真理値表 N=21,m=2
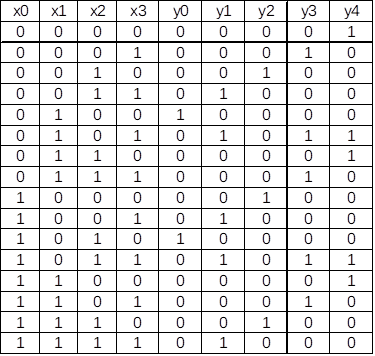
4.QISkitプログラム実装
QISkitによる実装プログラムは下記の通り.オラクルの記述は,参考文献2)では試行錯誤により論理回路の簡略化を行っているが,一行ずつ自動的に変換する方法とした.
以下プログラムに従って処理内容を説明する.
(1)ライブラリのインポート
from qiskit import *
from qiskit.circuit.library.standard_gates import C3XGate, C4XGate,MCXGate
from qiskit.tools.visualization import *
from qiskit import execute, Aer
from fractions import gcd, Fraction # for shor
import math
import matplotlib.pyplot as plt
from qiskit import IBMQ, QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute, Aer
from qiskit.qasm import pi
from qiskit.tools.visualization import plot_histogram
from qiskit import IBMQ, transpile
from qiskit.providers.ibmq.managed import IBMQJobManager
from qiskit.quantum_info import Statevector
from qiskit.circuit.library import RYGate
from qiskit.circuit.add_control import add_control
import numpy as np # np.dot(x, y)
(2)IQFT関連プログラム
参考文献2)を使用させていただいた.
def Swap(qci,s1,s2):
qci.cx(s1,s2)
qci.cx(s2,s1)
qci.cx(s1,s2)
def iqft(qci, q, n):
for i in range(n):
for j in range(i):qci.cu1(-math.pi/float(2**(i-j)), q[i], q[j])
qci.h(q[i])
(3)因数分解対象N, mの設定
N,mが互いに素であることは確認している.
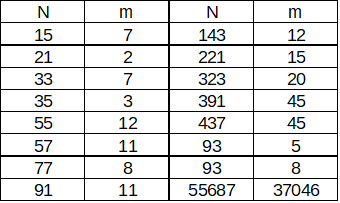
現在下記の組み合わせは確認している.現在の設定では最大のNは60000(2**16)程度.
表1 確認済組み合わせ(再掲)
while 1:
N = int(input('Enter an integer N: '))
print('You entered : ', N)
m = int(input('Enter an integer m: '))
print('You entered : ', m)
if gcd(N,m) ==1:
break
(4)レジスタの設定
N=50000程度を想定し設定している.
bx=9
print(bx)
by=16
print(by)
cn=by
qx = QuantumRegister(bx)
qy = QuantumRegister(by)
c = ClassicalRegister(cn)
qcx = QuantumCircuit(qx, c)
qcy = QuantumCircuit (qy, c )
qc=qcx+qcy
(5)オラクルの記述
一行ずつ自動的に変換している.
for i in range(bx):
qc.h(qx[i])
for i in range(2**bx):
X=i
for j in range(bx):
if (X & 2**(bx-1))==0:
qc.x(qx[j])
X=X<<
Y=(m**i)%N
for j in range(by):
if (Y & 2**bx)!=0:
if bx==3:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qy[j]])
elif bx==4:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qy[j]])
elif bx==5:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qy[j]])
elif bx==6:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qy[j]])
elif bx==7:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qy[j]])
elif bx==8:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qy[j]])
elif bx==9:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qy[j]])
elif bx==10:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qx[9],qy[j]])
elif bx==11:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qx[9],qx[10],qy[j]])
else:
print("bx is too large")
Y=Y<<1
X=i
for j in range(bx):
if (X & 2**(bx-1))==0:
qc.x(qx[j])
X=X<<1
(6)IQFTの実行
参考文献2)を使用させていただいた.
iqft(qc, qx, bx)
if bx==3:
Swap(qc, qx[0], qx[2])
elif bx==4:
Swap(qc, qx[0], qx[3])
Swap(qc, qx[1], qx[2])
elif bx==5:
Swap(qc, qx[0], qx[4])
Swap(qc, qx[1], qx[3])
elif bx==6:
Swap(qc, qx[0], qx[5])
Swap(qc, qx[1], qx[4])
Swap(qc, qx[2], qx[3])
elif bx==7:
Swap(qc, qx[0], qx[6])
Swap(qc, qx[1], qx[5])
Swap(qc, qx[2], qx[3])
elif bx==8:
Swap(qc, qx[0], qx[7])
Swap(qc, qx[1], qx[6])
Swap(qc, qx[2], qx[5])
Swap(qc, qx[3], qx[4])
elif bx==9:
Swap(qc, qx[0], qx[8])
Swap(qc, qx[1], qx[7])
Swap(qc, qx[2], qx[6])
Swap(qc, qx[3], qx[5])
elif bx==10:
Swap(qc, qx[0], qx[9])
Swap(qc, qx[1], qx[8])
Swap(qc, qx[2], qx[7])
Swap(qc, qx[3], qx[6])
Swap(qc, qx[4], qx[5])
elif bx==11:
Swap(qc, qx[0], qx[10])
Swap(qc, qx[1], qx[9])
Swap(qc, qx[2], qx[8])
Swap(qc, qx[3], qx[7])
Swap(qc, qx[4], qx[6])
else:
print("bx is too large")
exit()
fig=qc.draw(fold=-1)
# print(fig)
(7)シミュレーションの実行
for i in range(bx):
qc.measure ( qx[bx-1-i] , c[i] )
backend_sim = Aer.get_backend('aer_simulator')
r = execute(qc,backend_sim, shots=4096*4).result()
rc = r.get_counts()
print(rc)
図1にIQFT実行後のシミュレーション結果を示す.
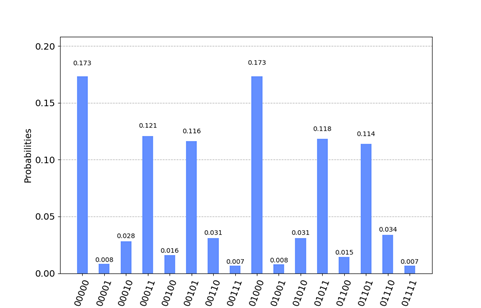
図1 IQFT後の量子ビット|x>の観測結果
(8)位相推定と因数分解処理
以下の推定は主に参考文献1)を参考に行った.
1)IQFT後の量子ビット|x>のピーク値検出
IGFT後の出現割合が0.05程度以上の量子ビット|x>を検出.
図1の場合は下記.
m=0,3,5,8,11,13
2)位数の推定
Mと位数rには下記の関係がある.
上記に位相推定結果を代入すると,下記のように位数r=6としたときの結果とほぼ一致する.
したがって,位数r=6と推定できる.
プログラムでは,n=0,1,2,3,4,5とm=0,3,5,8,11,13とを最小二乗法で直線補間し,その傾きaから位相 r=round((2**bx)/a)としている.図2に直線補間した結果を示す.
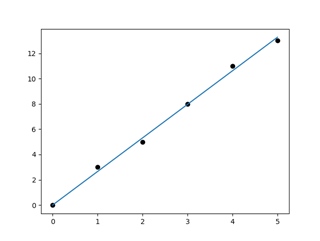
図2 n, m間の直線補間
x = []
y = []
j=0
for i in r.get_counts():
c=rc.get(i)
if c > 600:
x.append(j)
y.append(int(i,2))
j=j+1
y.sort()
print(x)
print(y)
xx = np.array(x)
yy = np.array(y)
def reg1dim(x, y):
a = np.dot(x, y)/ (x**2).sum()
return a
a = reg1dim(xx, yy)
r=round((2**bx)/a)
print(r)
3)素因数の計算
参考文献2)を参考に作成した.手順は下記.
p=m**(r/2)-1
q=m**(r/2)+1
pp=gcd(p,N)
qq=gcd(q,N)
print("N=",N," m=",m," r=",r)
print("p=",int(pp))
print("q=",int(qq))
・直線補間図出力
出力結果は図2.
plt.scatter(xx, yy, color="k")
plt.plot([0,xx.max()], [0, a * xx.max()]) # x.max()
plt.show()
・IQFT実行後のシミュレーション結果出力
出力結果は図1.
plt=plot_histogram (rc, figsize = (12,7))
plt.show()
[参考]
コメントのない実行ファイルを添付しておきます.
from qiskit import *
from qiskit.circuit.library.standard_gates import C3XGate, C4XGate,MCXGate
from qiskit.tools.visualization import *
from qiskit import execute, Aer
from fractions import gcd, Fraction # for shor
import math
import matplotlib.pyplot as plt
from qiskit import IBMQ, QuantumCircuit, ClassicalRegister, QuantumRegister
from qiskit import execute, Aer
from qiskit.qasm import pi
from qiskit.tools.visualization import plot_histogram
from qiskit import IBMQ, transpile
from qiskit.providers.ibmq.managed import IBMQJobManager
from qiskit.quantum_info import Statevector
from qiskit.circuit.library import RYGate
from qiskit.circuit.add_control import add_control
import numpy as np
def Swap(qci,s1,s2):
qci.cx(s1,s2)
qci.cx(s2,s1)
qci.cx(s1,s2)
def iqft(qci, q, n):
for i in range(n):
for j in range(i):qci.cu1(-math.pi/float(2**(i-j)), q[i], q[j])
qci.h(q[i])
while 1:
N = int(input('Enter an integer N: '))
print('You entered : ', N)
m = int(input('Enter an integer m: '))
print('You entered : ', m)
if gcd(N,m) ==1:
break
bx=9
print("bx=",bx)
by=16
print("by=",by)
cn=by
qx = QuantumRegister(bx)
qy = QuantumRegister(by)
c = ClassicalRegister(cn)
qcx = QuantumCircuit(qx, c)
qcy = QuantumCircuit (qy, c )
qc=qcx+qcy
for i in range(bx):
qc.h(qx[i])
for i in range(2**bx):
X=i
for j in range(bx):
if (X & 2**(bx-1))==0:
qc.x(qx[j])
X=X<<1
Y=(m**i)%N
for j in range(by):
if (Y & 2**bx)!=0:
if bx==3:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qy[j]])
elif bx==4:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qy[j]])
elif bx==5:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qy[j]])
elif bx==6:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qy[j]])
elif bx==7:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qy[j]])
elif bx==8:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qy[j]])
elif bx==9:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qy[j]])
elif bx==10:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qx[9],qy[j]])
elif bx==11:
qc.append(MCXGate(bx),[qx[0],qx[1],qx[2],qx[3],qx[4],qx[5],qx[6],qx[7],qx[8],qx[9],qx[10],qy[j]])
else:
print("bx is too large")
Y=Y<<1
X=i
for j in range(bx):
if (X & 2**(bx-1))==0:
qc.x(qx[j])
X=X<<1
iqft(qc, qx, bx)
if bx==3:
Swap(qc, qx[0], qx[2])
elif bx==4:
Swap(qc, qx[0], qx[3])
Swap(qc, qx[1], qx[2])
elif bx==5:
Swap(qc, qx[0], qx[4])
Swap(qc, qx[1], qx[3])
elif bx==6:
Swap(qc, qx[0], qx[5])
Swap(qc, qx[1], qx[4])
Swap(qc, qx[2], qx[3])
elif bx==7:
Swap(qc, qx[0], qx[6])
Swap(qc, qx[1], qx[5])
Swap(qc, qx[2], qx[3])
elif bx==8:
Swap(qc, qx[0], qx[7])
Swap(qc, qx[1], qx[6])
Swap(qc, qx[2], qx[5])
Swap(qc, qx[3], qx[4])
elif bx==9:
Swap(qc, qx[0], qx[8])
Swap(qc, qx[1], qx[7])
Swap(qc, qx[2], qx[6])
Swap(qc, qx[3], qx[5])
elif bx==10:
Swap(qc, qx[0], qx[9])
Swap(qc, qx[1], qx[8])
Swap(qc, qx[2], qx[7])
Swap(qc, qx[3], qx[6])
Swap(qc, qx[4], qx[5])
elif bx==11:
Swap(qc, qx[0], qx[10])
Swap(qc, qx[1], qx[9])
Swap(qc, qx[2], qx[8])
Swap(qc, qx[3], qx[7])
Swap(qc, qx[4], qx[6])
else:
print("bx is too large")
exit()
fig=qc.draw(fold=-1)
# print(fig)
for i in range(bx):
qc.measure ( qx[bx-1-i] , c[i] )
backend_sim = Aer.get_backend('aer_simulator')
r = execute(qc,backend_sim, shots=4096*4).result()
rc = r.get_counts()
print(rc)
x = []
y = []
j=0
for i in r.get_counts():
c=rc.get(i)
if c > 600:
x.append(j)
y.append(int(i,2))
j=j+1
y.sort()
print(x)
print(y)
xx = np.array(x)
yy = np.array(y)
def reg1dim(x, y):
a = np.dot(x, y)/ (x**2).sum()
return a
a = reg1dim(xx, yy)
r=round((2**bx)/a)
print("r=",r)
p=m**(r/2)-1
q=m**(r/2)+1
pp=gcd(p,N)
qq=gcd(q,N)
print("N=",N," m=",m," r=",r)
print("p=",int(pp))
print("q=",int(qq))
plt.scatter(xx, yy, color="k")
plt.plot([0,xx.max()], [0, a * xx.max()])
# plt.show()
plt=plot_histogram (rc, figsize = (12,7))
# plt.show()
5.おわりに
ショアのアルゴリズムをある程度自動的に可能なプログラムを作成した.しかし,mは試行錯誤的に行う必要がある.mの自動的検出は今後の課題である(かなり難しいか?).
参考文献
(1)ショアのアルゴリズムで21を素因数分解!量子コンピューターの基礎から解説!
(2)中山茂:Python 量子プログラミング入門(Gaia教育シリーズ8)