母集団と標本
調査を行う対象の全体を「母集団」、母集団から抽出された一部分を「標本」という
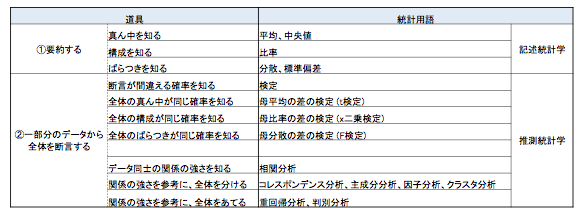
統計学の全体像
記述統計学
- 真ん中を知る (平均・中央値)
- 構成を知る (比率)
- ばらつきを知る (分散・標準偏差)
推測統計学
一部のデータから全体を推測する手法
断言が間違える確率を知る (検定)
検定とは「一部のデータであることによるブレを考慮しても、このデータ間には差があるといえるのか?」を確認するための手法
- 平均の差を検定 -> t検定
- 比率の差を検定 -> x二乗検定
- 分散の差を検定 -> F検定
データ同士の関係の強さを知る
仮説
「ある原因」が「ある結果」に影響するというような影響の仕組みについて考えること
- データ分析を始める前に、経験や既知の情報を参考に因果関係を考える
- 因果関係について、情報把握出来るようにデータを収集する
- とれたデータを見る
- とれたデータを見る限り、想像したような影響関係になっているか
- 4でなっている場合に【道具】を使い調べたい調査対象の全員についてどうなっているかを検証していく
仮説の分類
- AがBという状態だとCはDという状態になる
- AがBという状態になるとCはDに変化する
- AがBに変化するとCはDという状態になる
- AがBに変化するとCはDに変化する
また、このパターンを考える際に、数値を次の2つに分類して考えると、イメージしやすくなる
- 数値データ
- 連続値 (身長、体重、売上、テストの点数etc...)
- 種類データ (カテゴリカルデータ)
- 離散値 (血液型、性別、携帯電話の利用事業者等)
注意点
- 検定では、原因と結果との厳密な因果分析は出来ない
- データが少いと役に立たない
- 検定結果が優位となった(仮説は数学的に絶対正しい)とまでは言えない
- 巷で思われているほどには、有益な情報が得られる分析手法ではない
参考文献
こちらもあわせて紹介
