どんなものができる?
こんな感じのものが実装出来ます。
点の数、球の半径などが指定可能。

※この処理はあくまで点を均等っぽく並べる処理です!
数値解析や精密な計算とかには不向きなので注意。
黄金角を利用して点を球面上に並べる
【黄金比・黄金角による点群生成機構の解明・一般化】
論文:https://www.kyushu-u.ac.jp/f/59069/24_10_04.pdf
こちらの論文を参考にさせていただきました。
黄金角の方法についてザックリ説明
(※1) 黄金角の方法
円周率 2πを 1 : (1 + √5)⁄2(黄金比)に分割して得られる小さい方の角度。すなわち、𝜑 = 4𝜋⁄(3 + √5) ≒ 137.5度が黄金角。黄金角ずつ回転させながら、単位面積当たりの点の数が一定となるよう(※7 も参照)回転中心からの距離を調整して点群を配置する方法を黄金角の方法という。例えば、円盤の面積が点数𝑛に比例するように取る場合、円盤の半径は√𝑛に比例するので、円盤状に点群を生成するフォーゲル螺旋の式は(√𝑛 cos𝜑 , √𝑛 sin𝜑)となる。
要は、1/1.618...(黄金比)の角度ずつ、点を回転させて並べようという処理。(だと思う)
回転中心からの距離を少しずつ調整しながら点を並べていくと、以下のような点群が出来るらしい。きれい。

Unityに落とし込む
回転中心をとりあえずY軸とする。そうなると計算に必要なのはそれぞれの点のY座標と回転中心からの距離の主に2つとなるが、XZ平面上での中心からの距離は、
↓の通り、中心点からのY座標の距離と円の半径さえ分かっていれば求められる。
(|y|は中心からのy座標距離、rは求めたいXZ平面上の半径、Rは円(実装上では)の半径)
|y|^{2}+ r^2 = R^2
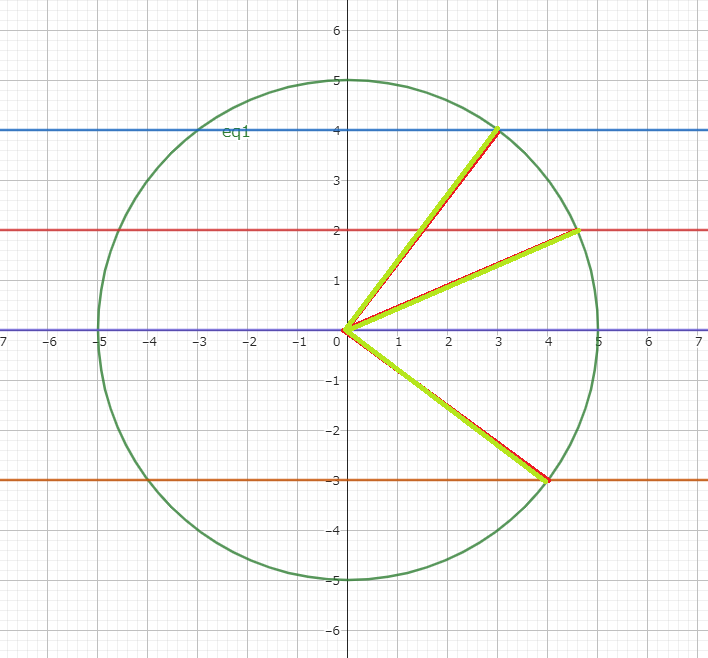
ということは、あと必要なのは点のY座標の位置だけ!になるのだが、あくまで今回は均等っぽく並べたいだけなので、Y座標は-RからRまでを点の数で分割しただけのものにする。
(もう少しちゃんとしたい!という人は各々がんばって!私には思いつきませんでした)
実際のコード
void GenerateSphericalPointCloud() {
/* 黄金角の計算 */
float phi = (1 + Mathf.Sqrt(5)) / 2; // 黄金比
float phiAngle = 2 * Mathf.PI / phi; // 黄金角
/* 点群を生成 */
for(int i = 0; i < pointNum; i++) {
/* 点の位置を算出 */
float y = radius - (i / (float)(pointNum - 1) * radius) * 2; // -RからRまでの範囲で均等に
float r = Mathf.Sqrt(radius * radius - y * y); // XZ平面上の半径を計算
float theta = phiAngle * i; // 黄金角で回転させる
float x = r * Mathf.Cos(theta); // X座標
float z = r * Mathf.Sin(theta); // Z座標
Vector3 pointPos = transform.position + new Vector3(x, y, z);// 点の位置
/* Cubeを生成 */
GameObject pointObj = GameObject.CreatePrimitive(PrimitiveType.Cube);
/* Transform設定 */
pointObj.transform.position = pointPos;
pointObj.transform.localScale = new Vector3(0.1f, 0.1f, 0.1f);
/* 色設定 */
pointObj.GetComponent<MeshRenderer>().material.color = Color.yellow;
}
}
コードにしてみるとかなりシンプル。
(実際の黄金角の方法からだいぶ簡略化したのもあるけど)
成果物
実際には自主制作ゲームでの爆発エフェクト代わりに使用しました。パーティクルシステムでいいじゃんと言えばそうなんだけども……。
球面上に点を並べる処理というより、オブジェクトを放射状に拡散する処理として考えたほうが使い勝手がいいかも……?
参考情報
【黄金比・黄金角による点群生成機構の解明・一般化】