ハローみなさん!! 今日も元気に周りの人と衝突してますか!!!!!
毎日のように様々な衝突を生み出すみなさん、そんな皆さんが衝突と聞いてすぐに頭に浮かぶのは、もちろん UUID であることでしょう。UUID のうち多く使われるのは version 4 だと思いますが、この ver. 4の UUID は、基本的にランダムな値として生成されます。
その結果として
- UUID って、オレと同じように周りと衝突してしまわないかな?
- 衝突した結果、余計な混乱を生み出さないかな?
- 今は周囲とたくさん衝突してしまう UUID も 30 代くらいになったら丸くなり誰もが慕う素敵な UUID にならないかな???
とベッドの中で夜も眠れずご心配の日々をお過ごしではないでしょうか。
乱数から生成されるんだったらその一意性って完全じゃないよね?
でも、結構みんな一意だと思って使ってるよね?
というわけで、一体ぼくたちは、どれだけの衝突確率を「無いもの」として扱っているのかを考えてみたいと思います。
結論
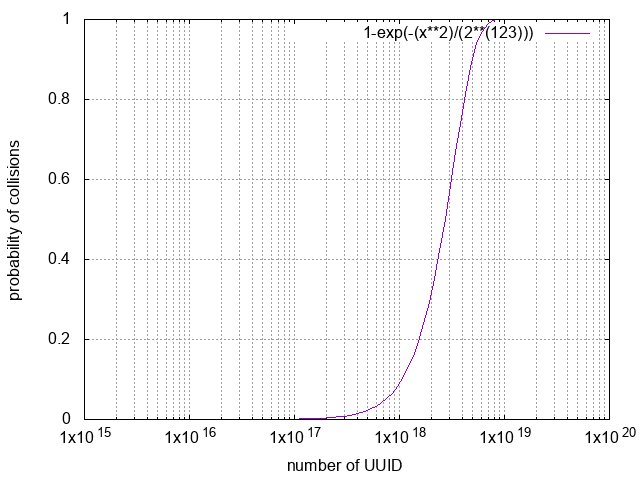
過程をすっ飛ばして結論を先に言いますと、$ n $ 回 UUID を生成したときに衝突が発生する確率は、およそ $$ 1-\exp\left(-\frac{{n}^2}{2^{123}}\right) $$ くらいになります。
試行回数に対する衝突確率の伸びをグラフ化するとこんなかんじ。$ x $ 軸は log scale になってることにご注意ください。
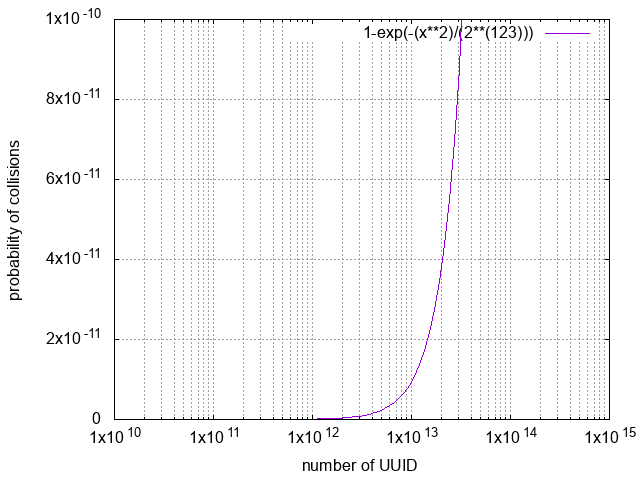
めちゃくちゃ拡大してみます。
過程
前提
UUID は 128 bit から構成されますが、Version 4 ではこの 128 bit のうち、122 bit にランダムな数値をセットして UUID とします (残りの 6 bit は固定値です)。
定式化
上記を前提に、ここでは、「version 4 で $ n $ 回 UUID を生成したとき、それらが 1 つでも衝突してしまう確率 $ P $」を求めます。
"1 つでも"というところからピンと来ると思いますが、これは "衝突が一切発生しない" という事象に対する背反事象になります。
このため、まずは衝突が一切発生しない確率をもとめ、それを 1 から引くという考え方をするのが王道です。
計算
順を追って考えましょう。
- $ n $回の試行のうちの、最初の 1 回目を考えます。このとき、衝突する UUID は存在しないので、衝突しない確率は 1 (100 %) です。
- $ n $ 回の試行のうちの、2 回目を考えます。このとき、1 回目に生成した UUID と衝突する可能性があります。UUID として発生し得るパターンは $ 2^{122} $ パターンあるので、衝突する確率は $ \frac{1}{2^{122}} $ になり、衝突しない確率は $ 1-\frac{1}{2^{122}} $ になります。
- $ n $ 回の試行のうちの、3 回目を考えます。このとき、1 回目に生成した UUID、あるいは 2 回目に生成した UUID と衝突する可能性があります。したがって、衝突する確率は $ \frac{2}{2^{122}} $ になり、衝突しない確率は $ 1-\frac{2}{2^{122}} $ になります。
- ...
- $ n $ 回の試行のうちの、$ n $ 回目を考えます。このとき、1 回目から $ n-1 $ 回目に生成した UUID と衝突する可能性があります。したがって、衝突する確率は $ \frac{n-1}{2^{122}} $ になり、衝突しない確率は $ 1-\frac{n-1}{2^{122}} $ になります。
以上から、n 回の試行において衝突が一切発生しない確率は、
$$ 1 \cdot \left(1-\frac{1}{{2}^{122}}\right) \cdot \left(1-\frac{2}{{2}^{122}}\right) \cdots \left(1-\frac{n-1}{{2}^{122}}\right)=\prod_{i=1}^{n-1}\left(1-\frac{i}{{2}^{122}}\right) $$
ということになり、衝突が発生する確率 $ P $ は、1 からこの確率を引いた、$$ P=1-\prod_{i=1}^{n-1}\left(1-\frac{i}{2^{122}}\right) $$ として表されます。
近似しましょう
で、こんな式を見せられても、実値を計算するのがマジでダルい。$ n $ が $10^{10}$ だったらどうやって計算するんや。
というわけで、近似しましょう。$ 1-\frac{i}{2^{122}} $ の項を何とかして綺麗にしてやりたい。
ここで、指数関数のテイラー展開を思い出すと、$ x \ll 1 $ のとき、$ {e}^{x} \approx 1 + x $ です。この指数関数のテイラー展開を利用すると、$$ 1-\frac{i}{{2}^{122}} \approx \exp\left(-\frac{i}{{2}^{122}}\right) $$ と近似できます。
これを $ P $ の式に代入し、おなじみの公式 $ \sum_{i=1}^{n-1}i=\frac{n(n-1)}{2} $を使うと、$$ P\approx 1-\exp\left(-\frac{1}{2^{122}}\frac{n(n-1)}{2}\right) $$ が導けます。
$ {n}^2 \gg n $ とすれば、$$ P\approx 1-\exp\left(-\frac{{n}^2}{{2}^{123}}\right) $$
になります。かなりきれいになりましたね。
じゃぁ衝突確率が p になるときの UUID 数 n はどのくらいなの
衝突が発生する確率 $P$ が $p$ になるための試行回数 $n$ を求めてみましょう。
$ 1-\exp\left(-\frac{{n}^2}{2^{123}}\right) \approx p $ を $n$ に対して解けば良いです。
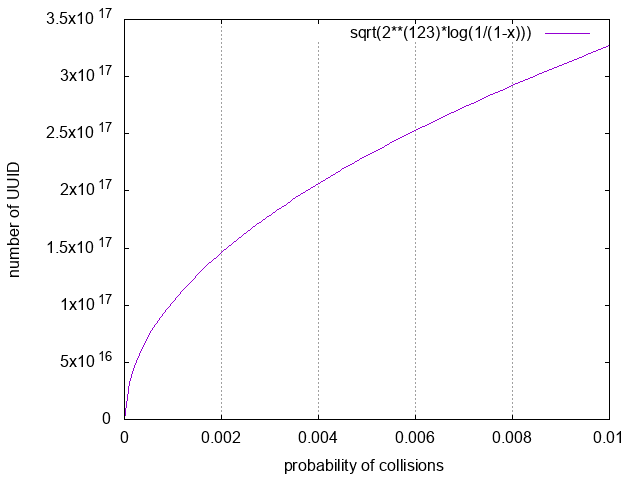
これ、わりとかんたんで、$n\approx \sqrt{2^{123} \ln{\frac{1}{1-p}}}$ になります。
たとえば、UUID を $ 3 \times 10^{17}$ 回くらいつくると、1 % ($p=0.01$) の確率で衝突するってことですね。
この衝突確率を現実的に考慮すべきリスクととるか否か、まぁ状況には依るのかもしれません。ちなみに宝くじで 1 等が当選する確率は 2,000 万分の 1 くらいだとか。
背景にある問題
じつはこの衝突確率を求める問題は、誕生日問題 と呼ばれる問題の 1 つです。
高校数学あたりで、クラスの 30 人のうち誕生日が一致する人がいる確率を求めなさい、的な問題を記憶されている方も多いのではないでしょうか。