この記事はNTTコミュニケーションズアドベントカレンダー12日目の記事です。
こちらの記事では、巷で話題の統計的因果探索の手法群を総合的に集めたlingamライブラリの紹介と、実際に利用した例を紹介します。この手法群の元祖かつ代表であるLiNGAMは様々なサイトで紹介されているので、今回は
- 未観測変数を考慮したBottomUpParceLiNGAM
- 非線形かつ未観測変数を考慮したCAM-UV
の2種についてLiNGAMプロジェクトの公式チュートリアルを参考に紹介します。さらに、巷のオープンデータに適用してみて考察を行います。なお、この記事では各手法の性質については記述しますが、理論的な背景や式の導出の解説はしませんので、あらかじめご了承ください(ここから先は自分の目で(以下略))
統計的因果探索とは
統計的因果探索は複数の仮定を基にデータから因果グラフを生成する手法のことです。主に離散変数をもとに因果効果を議論するRubin派ではなく、Pearl派、すなわちグラフを元に因果関係やその効果を議論する方の分野に属しています。
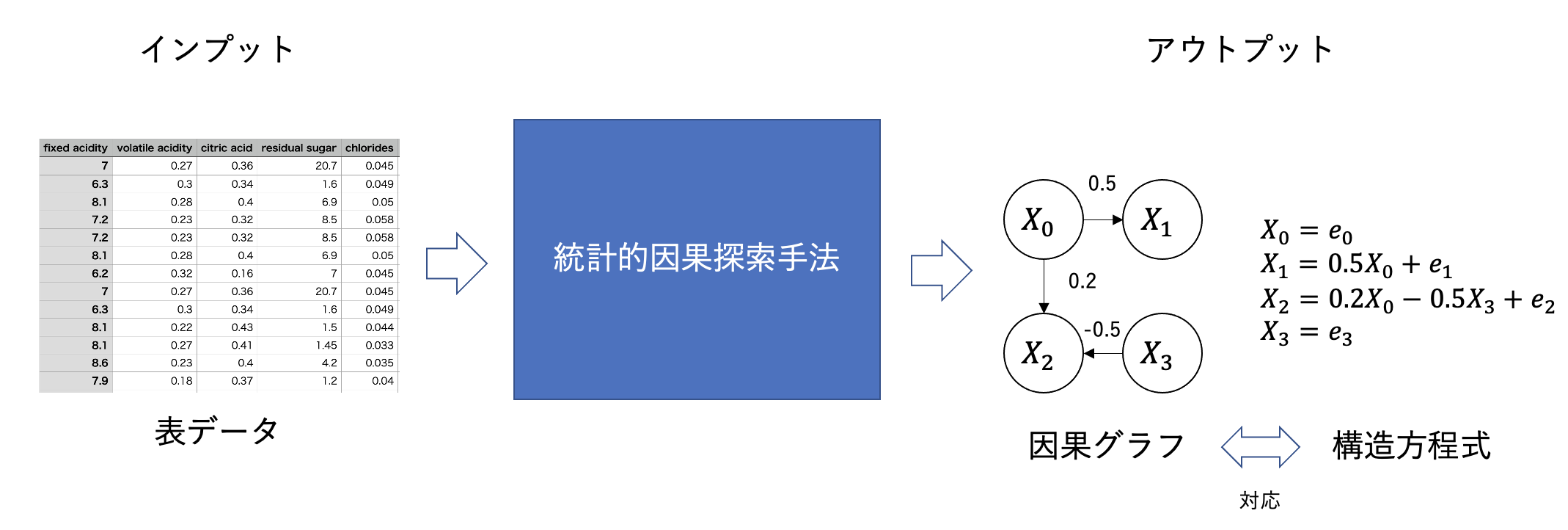
統計的因果探索は上記の図の通り、データを入力して、アウトプットとして因果グラフや因果の強さを与える構造方程式を識別する手法です。構造方程式とは、上の図で示されるようなXからYが生成される時の式とその因果的な順番を持つモデルとなります。
応用先としては、例えば化学系プラントで、操作する変数とその操作の結果として得られる製品品質などの目的となる変数がありそれぞれがセンサーデータとして得られているとします。このセンサーデータに統計的因果探索の手法を利用することで、どの操作変数を変更すれば品質に影響があるのかを突き止めることができます。それ以外でもマーケティングをはじめとする様々な分野で「原因はなんなのか?」を突き止めたいことはあるでしょう。そういう意味で統計的因果探索は様々な応用先のある素敵な手法だと言えます。
統計的因果探索の手法の研究対象としては仮定のバリエーションが挙げられます。例えば現実にデータが生成される背景が線形だったり、非線形だったり、ノイズがガウス分布だったり一様分布だったり、時系列モデルだったりすることがあります。
そういったデータの状況に応じた仮定をもとに、構造方程式モデルを定義します。例えばデータが非線形であることを仮定する手法では変数間の関係性を表す構造方程式は非線形モデルで表現されます。もちろん、様々な構造方程式と仮定を用意すれば良いだけではなく、データから構造方程式モデルを同定できること(識別可能性)を理論的に補償する必要があります。
以降ではいくつかの統計的因果探索の手法を紹介していきます。
LiNGAM
今回メインの2つの手法に触れる前にLiNGAMについても簡単に触れておきます。LiNGAMは統計的因果探索手法の中で最も利用されるアルゴリズムです。データの生成過程が線形かつデータに含まれるノイズが非ガウス、因果関係が非巡回という仮定のもと、データから因果構造が一意に決まることを保証し、最終的に線形の構造方程式を出力することができます。
lingamライブラリでも利用可能であり、前の説の図のように、表データを入力として線形の構造方程式を出力します。利用もskleanのモデルのようにデータをfitするだけです。
model = lingam.DirectLiNGAM()
model.fit(X) # X: 二次元(表)データ
アウトプットとして以下のように変数間の関係性を行列で返すことができます。
>>> print(model_lingam.adjacency_matrix_)
array([[ 0. , 0. , 0. , 0.506, 0. , 0. ],
[ 0.499, 0. , 0.495, 0.007, 0. , 0. ],
[ 0. , 0. , 0. , 0.791, 0. , 0. ],
[ 0. , 0. , 0. , 0. , 0. , 0. ],
[ 0.448, 0. , -0.451, 0. , 0. , 0. ],
[ 0.48 , 0. , 0. , 0. , 0. , 0. ]])
行は原因となる変数、列が結果となる変数を意味し、各要素が因果の強さ(回帰係数)、要素が0であればそれはその変数間の因果関係がないことを表します。
単純な線形構造であればLiNGAMでサクッと因果関係を出すことができます。一方、線形であったり、関連する全ての変数を含めている必要があるといった仮定を保つため、現実の問題に当てはめるにはうまくいかないこともあります。
このためにいくつかの派生系が提案されています。
BottomUpParceLiNGAM
まず、未観測な変数がある場合を考えてみます。例えば製品を作成したときの試験データとして硬度、温度、水分量があり、それぞれの因果関係を知りたいとします。この時、実は水分量と温度は試験データに含まれない外気温から強く影響を受けるとします。(外気温がいわゆる疑似相関を起こす変数)
この状態で硬度、温度、水分量の変数に対してLiNGAMを適用してしまうと、外気温の影響を考慮できないために得られる因果グラフや効果が正確に推定できません。こういった変数を未観測共通原因と呼びます。外気温であればアメダスなどから持ってくれば済むのですが、データとして取得できなかった変数が未観測共通原因になることもありえます。このような場合はどうすべきでしょうか?
BottomUpParceLiNGAMはこの解決のために未観測共通原因を考慮して因果グラフを推定できる手法です。仮定としてはLiNGAMと同様の線形、ノイズが非ガウス分布、非巡回のグラフであるに加えて、外生的(親を持っていないRootとなる変数)な変数のみが未観測共通原因を持っていることも加えています。
それでは実験データで実際に見てみましょう。今回は未観測共通原因として$X_6$を用意して$X_2, X_3$に因果関係があるデータを生成してみます。
np.random.seed(1000)
# 構造方程式
x6 = np.random.uniform(size=1000) # これを未確認共通原因とする
x3 = 2.0*x6 + np.random.uniform(size=1000)
x0 = 0.5*x3 + np.random.uniform(size=1000)
x2 = 2.0*x6 + np.random.uniform(size=1000)
x1 = 0.5*x0 + 0.5*x2 + np.random.uniform(size=1000)
x5 = 0.5*x0 + np.random.uniform(size=1000)
x4 = 0.5*x0 - 0.5*x2 + np.random.uniform(size=1000)
# 入力データにX6は含めないようにする
X = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T, columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
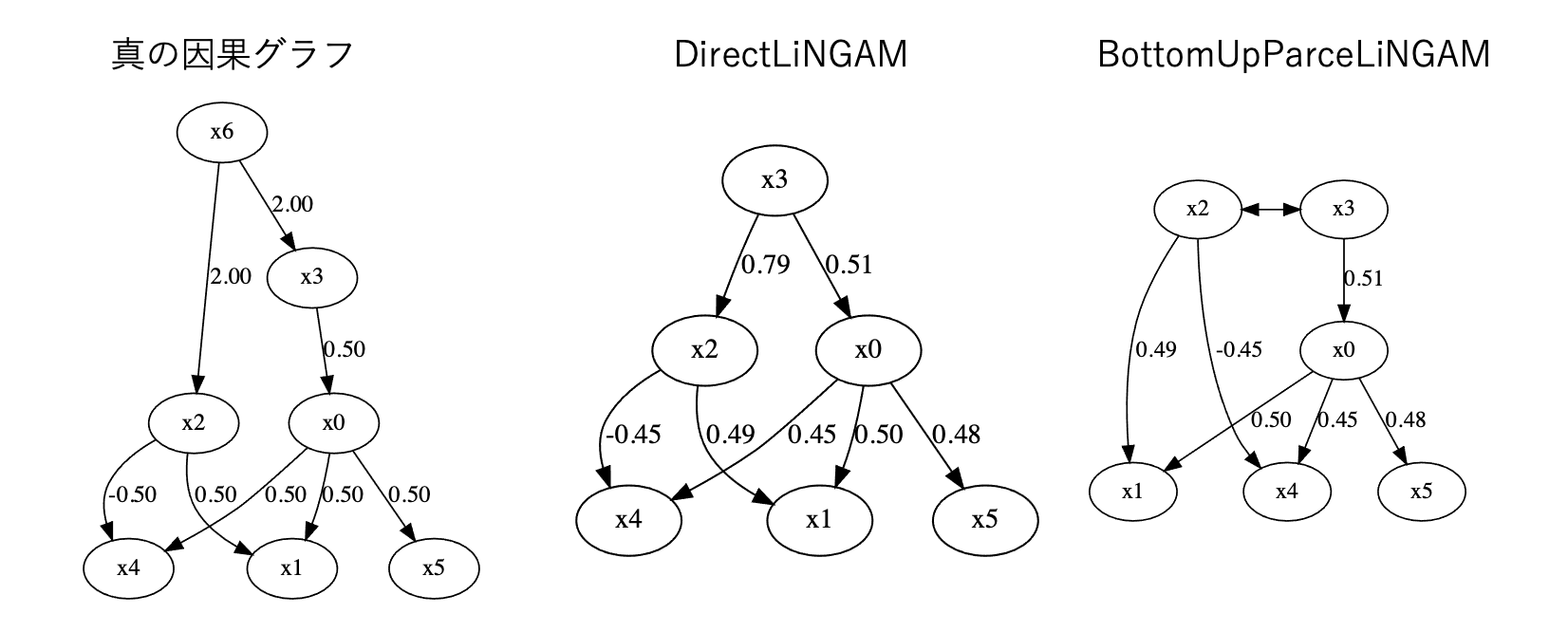
この$X_6$を抜いたデータに対して素のLiNGAM、BottomUpParceLiNGAMを実行した場合は上記のようになります。なお、実行は以下のコードで行います。
model = lingam.BottomUpParceLiNGAM()
model.fit(X) # fitするだけ
make_dot(model.adjacency_matrix_)
LiNGAMを利用した場合は$X_3$が$X_2$の親となってしまい、実際の因果関係とは変わってしまっています。BottomUpParceLiNGAMでは<->を使って未観測共通原因を持つ変数を表現することで正しい因果グラフが得られています。したがってLiNGAMを利用する場合と比べて未観測共通原因がある場合でも精度の高い推論ができていることがわかります。
CAM-UV
ここまでは線形の関係性を持つデータのみを扱ってきましたが、現実のデータは線形であるものだけではなく、非線形の関係性を持っている変数も存在します。特に自然科学の分野では自然の事象を非線形関数だったり微分方程式のようなもので表しています。このようなデータを扱う場合、今までの線形性を仮定している手法では正しい推定ができません。
CAM-UVは非線形の因果関係を持つデータに対して因果グラフを推定する手法です。加えて、未観測な変数があったとしてもそれに対応できる柔軟性も兼ね備えています。CAM-UVはデータに以下の仮定を置いています。
- 変数間の関係性は一般化加法モデル(GAM、非線形の回帰モデルの一つ)で表現できる
- 因果グラフは有効非巡回グラフ(DAG)で表現される
CAM-UVでは2種類の未観測変数を考慮することができます。
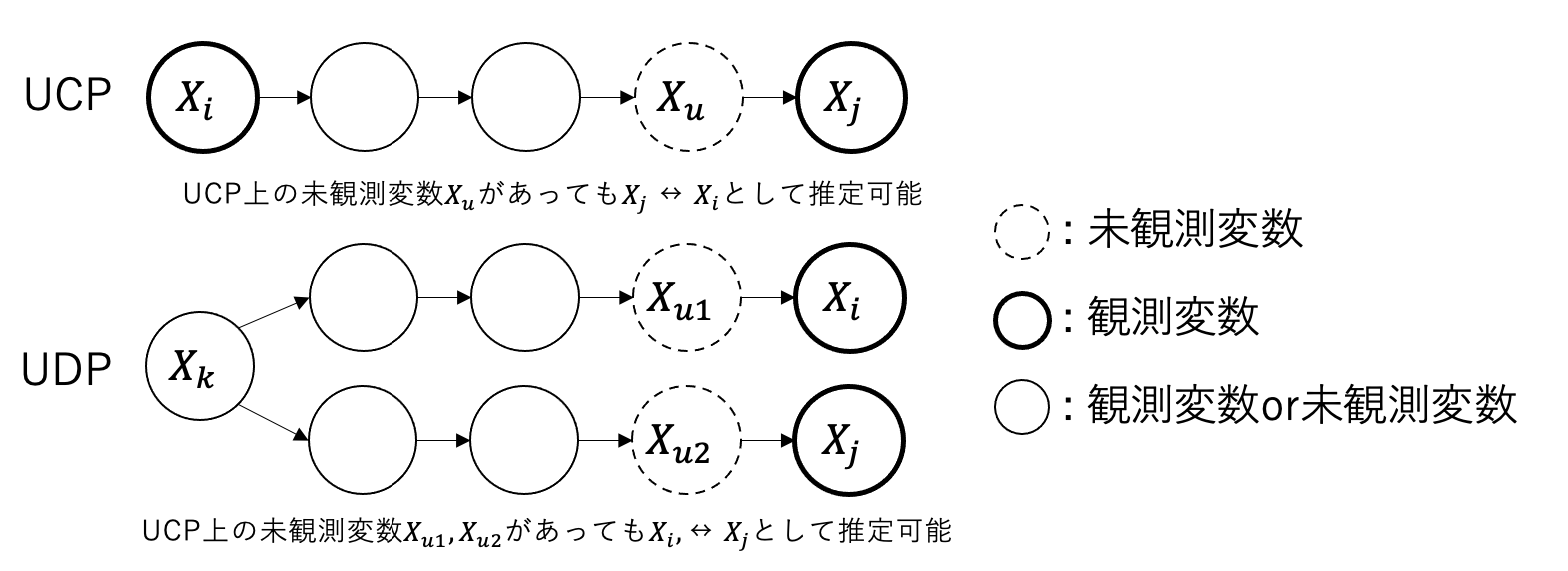
Unobserved Causal Path(UCP)とは、以下のようにある変数$X_i$からある変数$X_j$までの因果関係の中で途中に現れる未観測な変数が存在する場合のパスのことを言います。
Unobserved Backdoor Path(UBP)とは、2つの変数$X_i$、$X_j$に対してバックドアパスを開く(疑似相関を引き起こす)ような変数$X_k$があった場合、$X_k$から$X_i, X_j$の各変数までのパスの中に未観測な変数が存在するパスのことを言います。バックドアに関しては入門統計的因果推論が詳しいです。
上記の条件を満たすような未観測な変数があったとしてもCAM-UVは因果グラフを求めることができます。また、lingamライブラリではUCP、UDP上の変数に関してはいずれの場合も$X_i \leftrightarrow X_j$として表現されます。
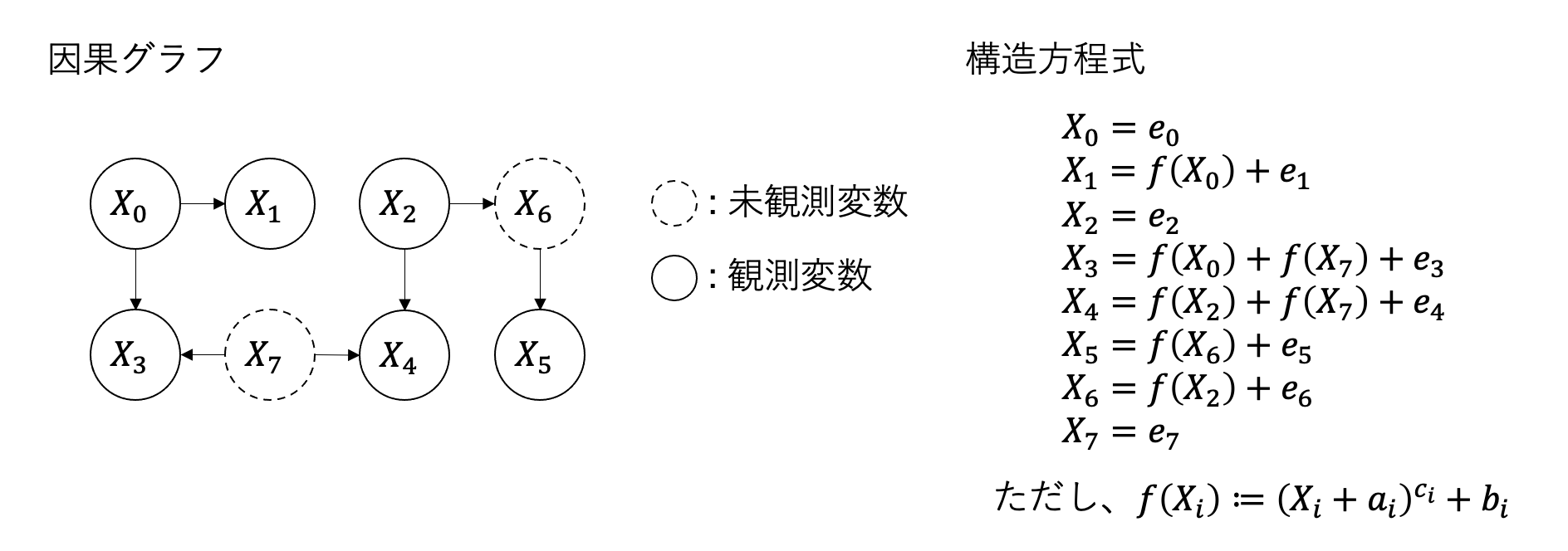
それではチュートリアルの例を見てみましょう。以下の因果グラフ、構造方程式からデータを生成します。未観測変数である$X_6$、$X_7$が含まれていることに注意してください。それぞれUCP上、UDP上の未観測変数となります。
生成するためのコードは以下です。
# チュートリアルのデータ生成を引用
def get_noise(n):
noise = ((np.random.rand(1, n)-0.5)*5).reshape(n)
mean = get_random_constant(0.0,2.0)
noise += mean
return noise
# 因果の関係性を表す非線形関数
# 今回は f(X) = (X + a)^c + b (a, b, cはそれぞれランダム変数)
def causal_func(cause):
a = get_random_constant(-5.0,5.0)
b = get_random_constant(-1.0,1.0)
c = int(random.uniform(2,3))
return ((cause+a)**(c))+b
def get_random_constant(s,b):
constant = random.uniform(-1.0, 1.0)
if constant>0:
constant = random.uniform(s, b)
else:
constant = random.uniform(-b, -s)
return constant
def create_data(n):
causal_pairs = [[0,1],[0,3],[2,4]]
intermediate_pairs = [[2,5]] # 2,5の間に未観測変数
confounder_pairs = [[3,4]] # 3,4には未観測共通原因
n_variables = 6
data = np.zeros((n, n_variables)) # observed data
confounders = np.zeros((n, len(confounder_pairs))) # data of unobserced common causes (x7)
# 各変数の加法ノイズ
for i in range(n_variables):
data[:,i] = get_noise(n)
for i in range(len(confounder_pairs)):
confounders[:,i] = get_noise(n)
confounders[:,i] = confounders[:,i] / np.std(confounders[:,i])
# 未観測共通原因からX3, X4への影響を追加
for i, cpair in enumerate(confounder_pairs):
cpair = list(cpair)
cpair.sort()
data[:,cpair[0]] += causal_func(confounders[:,i])
data[:,cpair[1]] += causal_func(confounders[:,i])
for i1 in range(n_variables)[0:n_variables]:
data[:,i1] = data[:,i1] / np.std(data[:,i1])
for i2 in range(n_variables)[i1+1:n_variables+1]:
# 観測変数の因果関係に沿って原因から結果へ加算
if [i1, i2] in causal_pairs:
data[:,i2] += causal_func(data[:,i1])
# X2, X5の間の未観測変数に対してX6の影響を加算
if [i1, i2] in intermediate_pairs:
interm = causal_func(data[:,i1])+get_noise(n)
interm = interm / np.std(interm)
data[:,i2] += causal_func(interm)
return data
sample_size = 2000
X = create_data(sample_size)
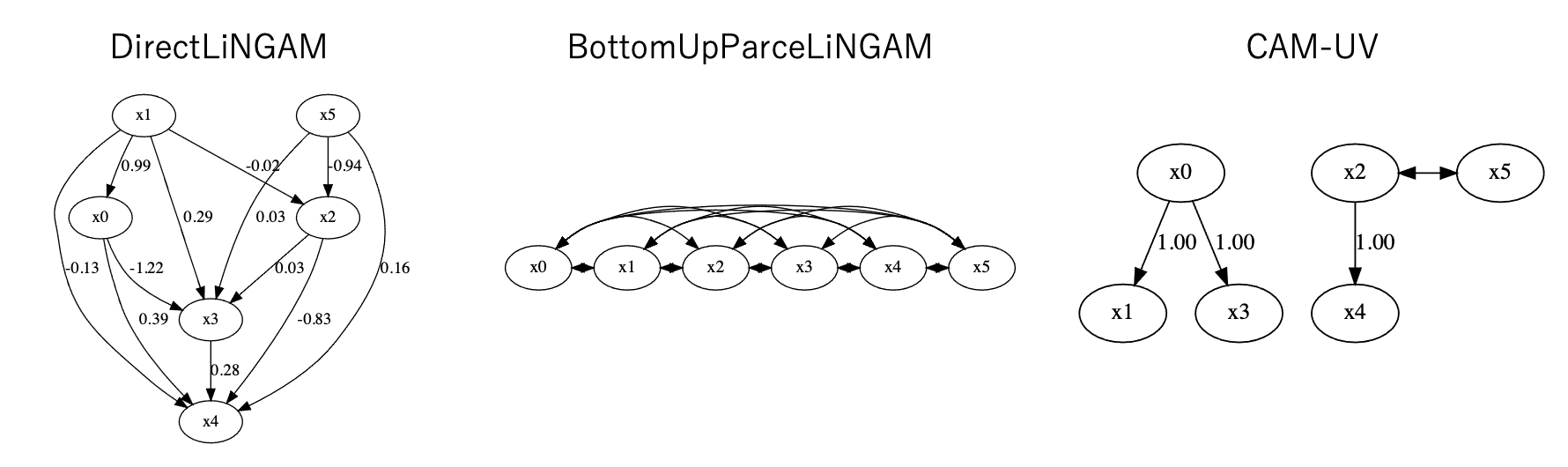
このデータから$X_6, X_7$を抜いたデータに対してLiNGAM、BottomUpParceLiNGAM、CAM-UVをそれぞれ実行して得られた結果は以下です。
LiNGAMは正解の因果グラフに比べてかなり変形したものになってしまいました。また、BottomUpParceLiNGAMは因果関係の発見に失敗しているようです。これらはまず非線形のデータに対して対応していないことと、未観測変数に対しても仮定を満たしていないことから精度の低い結果になったと思われます。
一方でCAM-UVはほとんど正解の因果グラフを当てられています。このようにCAM-UVは複雑な関係性を持つ因果グラフに対しても効果を発揮することができます。
これらの結果から、CAM-UVが最も良い手法なのでは?という読者の声も聞こえますが、一概にそうとも言えません。ここでは示していませんが、CAM-UVはGAMを利用しているためにLiNGAMと比べてかなり長い計算時間がかかります。また、非線形の因果関係は因果関係の強さという点では解釈が難しくなってしまうという欠点もあります。軽さを求めるか、正確性を求めるか、解釈性を求めるかなどのビジネス要件に応じて選択すべきです。
実データで試してみた
最後にこれらの手法を実データに適用してみて考察を行います。実データの場合Ground Truthがある場合はほとんどないので正当な評価が難しい(因果探索の研究の辛いところ)のですが、結果からある程度の考察を試みます。
今回はUCI repositoryの中からWine Qualityのデータに対して各手法を実行してみます。このオープンデータはポルトガル北部で生産された赤ワイン、白ワインの評価を集めたものです。特徴量としては酸味や糖度、塩化物、PHといった化学的に取得された11個の変数と人間がつけたスコア(quality)が10段階で評価されています。
今回は最終的な人間の評価であるqualityに対してどの変数が寄与しているのかを各手法で比べてみます。私は赤ワインよりも白ワインの方が好きなので、白ワインのデータを使います。全ての変数を利用するのは時間がかかるので、今回は5つの変数(酸味、残留糖度、アルコール度数、亜硫酸、評価)に絞って因果探索を行います。また、実行に時間がかかるので、500サンプルにサンプリングして実行します。
コードは以下です。
import lingam
import pandas as pd
from lingam.utils import make_dot
df = pd.read_csv('./data/winequality-white.csv', sep=';')
use_columns = ['fixed acidity', 'residual sugar', 'total sulfur dioxide', 'alcohol', 'quality'] # 今回は限定
use_df = df[use_columns]
# 正規化とサンプリング
norm_df = (use_df - use_df.mean(axis=0)) / use_df.std(axis=0)
norm_df = norm_df.sample(500)
# LiNGAM
model_lingam = lingam.DirectLiNGAM()
model_lingam.fit(norm_df)
# 因果グラフを表示
display(make_dot(model_lingam.adjacency_matrix_, labels=use_columns))
# BottomUpParceLiNGAM
model_bup = lingam.BottomUpParceLiNGAM()
model_bup.fit(norm_df)
display(make_dot(model_bup.adjacency_matrix_, labels=use_columns))
# CAM-UV
model_cam = lingam.CAMUV()
model_cam.fit(norm_df)
display(make_dot(model_cam._adjacency_matrix, labels=use_columns))
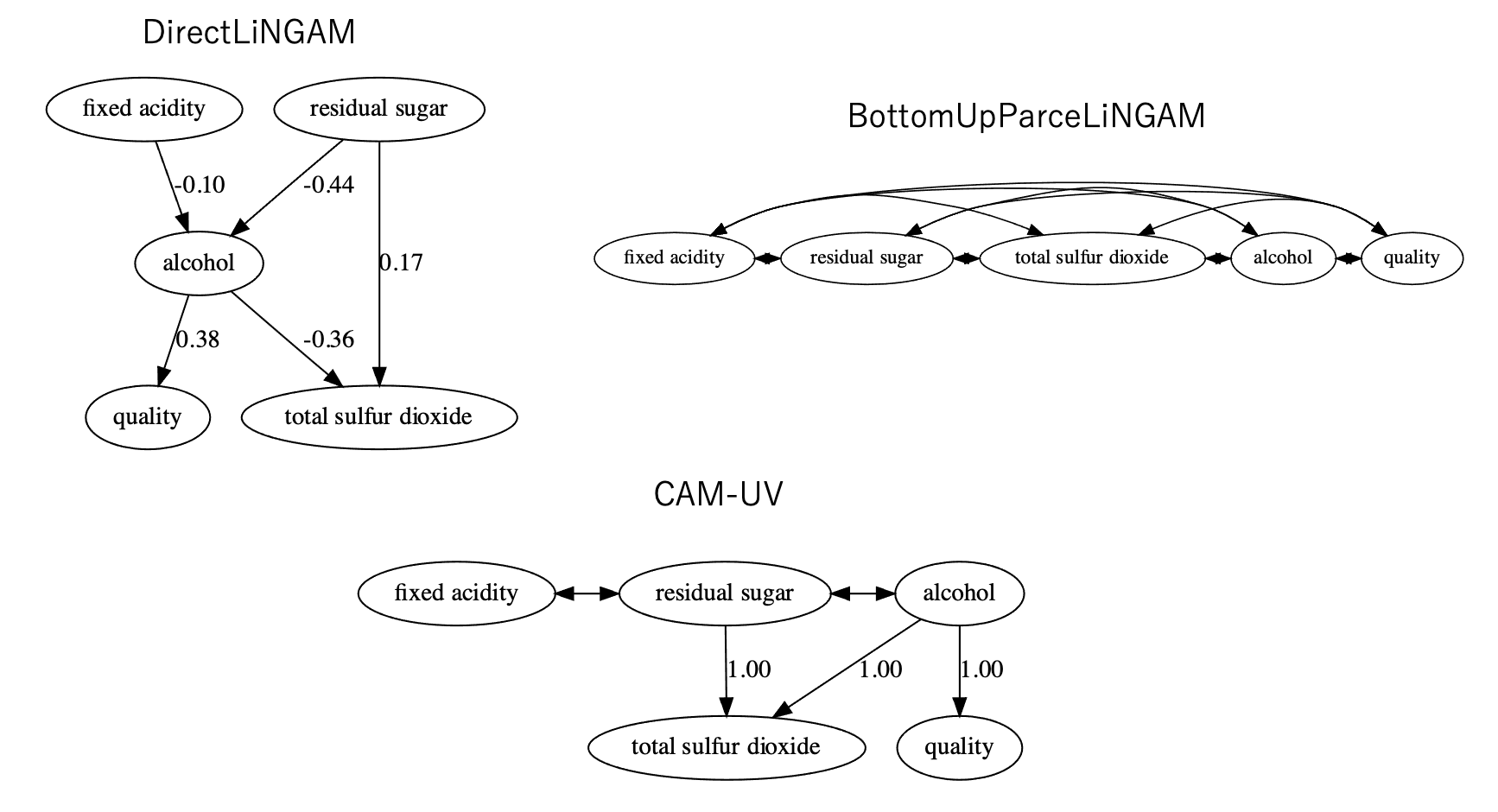
結果は以下の通りです。
LiNGAMとCAM-UVは似たような因果関係、BottomUpParceLiNGAMは仮定が重いせいもあってか、因果構造が推論できませんでした。結果の考察をしてみましょう。
結果としてはアルコール量が増えると全体の評価値が上がるという因果構造が推論できました。一方で、残留している糖が増えるとアルコールの量は少なくなってしまう関係性もLiNGAMから見てとれます。この関係性は発酵時の糖がアルコールに変化する過程を示しているようにも見えます。ワインの中に残留する糖が多いということは、それだけ糖からアルコールに転化する量が少なかったということになるので、負の因果関係を持っているのかもしれません。ただし、アルコール->糖という変化もありそうなので、一概には言えません。こういった係数による考察は線形で表されるLiNGAMの強みとも言えます。
また、LiNGAMは酸の濃度→アルコールという関係があるのに対して、CAM-UVではその線がなくなり、代わりに残留糖に対して両矢印が生えています。つまり、CAM-UVの方では酸の濃度と残留糖に対してUDP、UCPがあると考えられます。もしUDPであるとすれば、酸の濃度と残留糖には未観測共通原因が存在すると言えます。例えば、ブドウの品種は酸と糖度に関連する共通原因となりうるのでそれを表現している可能性もありますし、さらに土壌や場所なども関連するので、こういった変数を入れてみると面白いかもしれません。
今回は特にデータの仮定を調べずにまず手法を適用する方法を取りましたが、実際は変数の分布を調べてガウス分布かどうか確認したり、Bootstrap法で信頼度を測ったり、各因果関係の係数に対してp値を算出したりしてデータや因果関係をまず統計的に見ていくことが必要です。それを踏まえて良いモデルを選ぶことが重要です。
ちなみに今回の結果から言うとアルコール度数が高いワインの評価が高い、なのでアルコールを添加した(因果的には介入した)酒精強化ワインが最強なのではないかという結論を勝手に想像しました!
終わりに
今回は統計的因果探索手法の全体像と2つの手法について紹介しました。lingamライブラリは大変便利なので、もし因果関係を見てみたいという場合には真っ先に使ってみてください。それでは楽しい因果ライフを!
次のアドベントカレンダーの記事はMasaki Koshiさんです!
2024/12/1: 因果グラフの解釈が間違っていたので更新しました。
参考文献
- LiNGAMプロジェクト
- T. Tashiro, S. Shimizu, A. Hyvärinen, T. Washio. ParceLiNGAM: a causal ordering method robust against latent confounders. Neural computation, 26(1): 57-83, 2014.
- T. N. Maeda and S. Shimizu. Causal additive models with unobserved variables
- P. Cortez, A. Cerdeira, F. Almeida, T. Matos and J. Reis. Modeling wine preferences by data mining from physicochemical properties. In Decision Support Systems, Elsevier, 47(4):547-553, 2009.