回帰分析とは
簡単な例を用いて説明します!
あるお店で8月のアイスの売り上げについて分析することを考えます。
このとき、最高気温とアイスの売り上げの関係を表にまとめると以下のようになりました。

これをグラフ化すると以下のようになります。

最高気温が上がるにつれて、アイスの売り上げも良くなることが直感的にわかります。
さらに、この2変数の関係は直線的な関係(一次関数)になっていそうです。
そこで、最高気温とアイスの売り上げを直線的な関係(一次関数)で表してみます。
ある1日の最高気温を$x$,その日のアイスの売り上げを$y$と書くと、これらの関係は
y=ax+b \tag1
の形で表すことができます。しかし今、式$(1)$中の$a,b$は実際の数値がよくわからない変数です。もしも、これらの変数$a$,$b$を表のデータから推測できれば、今後の最高気温がわかると売り上げも式$(1)$の計算に従って推定することができます。
このように、表の数値データを使って関数$y=f(x)$を推定し、未知のデータ$x'$が与えられたときの予測結果$y'=f(x')$を出力する分析を回帰分析と言います。
実際の分析
では、実際に$a,b$をExcelで求めてみます。
Excelの「分析ツール」には回帰分析を行なってくれる機能が備わっています。
この機能を用いると以下のような出力がなされます。
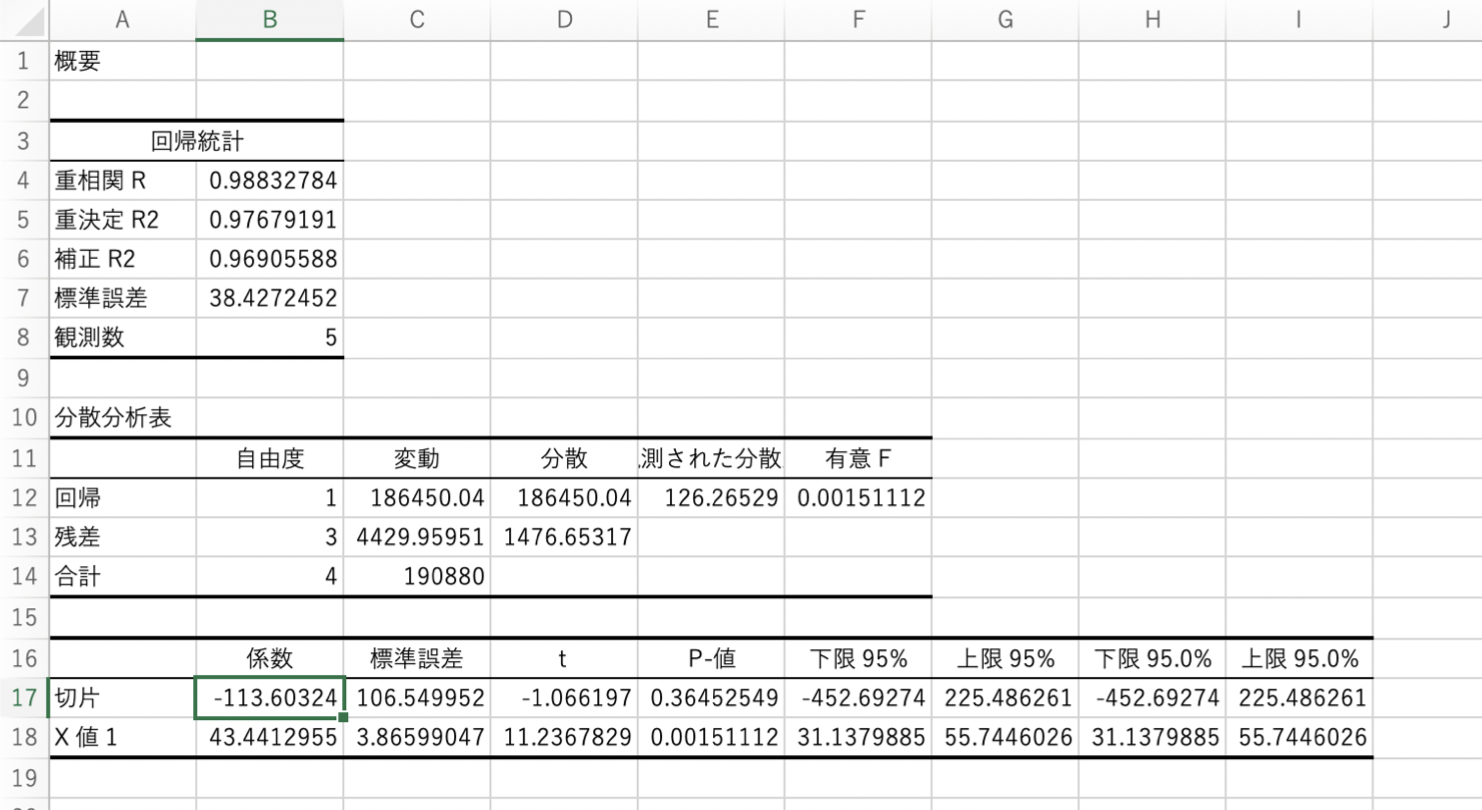
様々な数値がありますが、ここではB17セルとB18セルの値だけを見てみましょう。
B17の値が切片$b$、B18の値が傾き$a$です。つまり、今回の回帰直線は
y=43.4x-113.6 \tag2
ということになります!
1日の最高気温からアイスの売り上げを推定できる式ができました!
この直線をグラフにプロットすると以下のようになります。
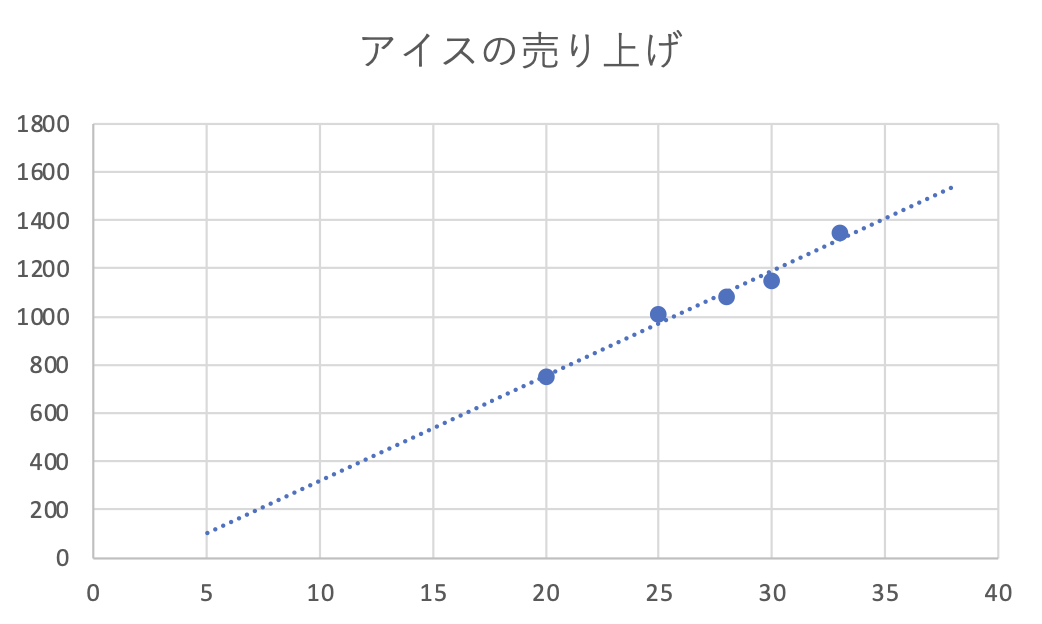
このように、もとのデータと近い位置に直線が通っていることがわかります。
もしも、最高気温38°Cの日のアイスの売り上げが知りたい場合は
43.4\times38-113.6=1535.6 \tag3
となるので、約1535本のアイスが売れると予測することができます。
単回帰の理論
得られたデータが$N$個あり、それらを$(x_i,y_i)$と書くことにします。$i=1,2,3,\dots,n$です。
このとき、単回帰モデルの式に$x_i$を代入したときの$y_i$の推定値$\hat{y_i}$は以下の式で書けます。
\hat{y_i}=ax_i+b \tag4
ここで、$y_i$と$\hat{y_i}$の意味の違いに注意してください。$y_i$は実際に観測されたデータで、$\hat{y_i}$は観測データ$x_i$を単回帰モデルに当てはめたときの推定値です。
単回帰モデルが実際のデータをより良く表すためには、$y_i$と$\hat{y_i}$の間の誤差が少なくなれば良いといえます。そこで、以下のような誤差関数$f$を考えます。
f(x_i,y_i)=\sum_{i=1}^{n}(y_i-\hat{y_i})^2=\sum_{i=1}^{n}(y_i-ax_i-b)^2 \tag5
この関数$f$で各誤差を二乗しているのは、誤差に正負があるためにそれらが打ち消されることを防ぐためです。
よってこの関数$f$の値が最も小さくなるように、$a,b$を定めれば良いということになります。
ここでは偏微分を用いて最適な回帰係数$a,b$を求める方法を軽く紹介します。
$a,b$を変数と見たとき、誤差関数の極値は、
\left\{
\begin{array}{ll}
\frac{\partial f}{\partial a} = 0\\
\frac{\partial f}{\partial b} = 0
\end{array}
\right.
\tag6
を満たします。そこで式$(5)$を式$(6)$に代入し計算を進めると、以下の連立方程式が導かれます。
\left\{
\begin{array}{ll}
\sum_{i=1}^{n} (y_i-ax_i-b)x_i = 0\\
\sum_{i=1}^{n} (y_i-ax_i-b) = 0
\end{array}
\right.
\tag7
連立方程式$(7)$を$a,b$について解くことで、
a = \frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sum_{i=1}^{n}(x_i-\bar{x})^2}
b = \bar{y}-a\bar{x}
と求まります。ここで$\bar{x},\bar{y}$はそれぞれ以下の定義です(標本平均と言います)。
\bar{x}=\frac{1}{N}\sum_{i=1}^{n}x_i \quad \bar{y}=\frac{1}{N}\sum_{i=1}^{n}y_i
このように、二乗誤差を最小化して回帰係数を求める手続きを最小二乗法といいます。
行列を用いた定式化
あらためて、単回帰の式は
\hat{y_i}=ax_i+b
ですが、これをデータ$i=1,2,\dots,n$について並べて、行列を作ってみます。
\begin{pmatrix}
\hat{y_1} \\
\vdots \\
\hat{y_n} \\
\end{pmatrix}
=
\begin{pmatrix}
ax_1+b \\
\vdots \\
ax_n+b \\
\end{pmatrix}
=
\begin{pmatrix}
x_1 & 1 \\
\vdots & \vdots \\
x_n & 1\\
\end{pmatrix}
\begin{pmatrix}
a\\
b\\
\end{pmatrix}
ここで以下のように定義します。
\boldsymbol{\hat{y}}=
\begin{pmatrix}
\hat{y_1} \\
\vdots \\
\hat{y_n} \\
\end{pmatrix}
\quad
\boldsymbol{X}=
\begin{pmatrix}
x_1 & 1 \\
\vdots & \vdots \\
x_n & 1\\
\end{pmatrix}
\quad
\boldsymbol{\beta}=
\begin{pmatrix}
a\\
b\\
\end{pmatrix}
このように書く利点は、本来$n$本ある方程式・2個ある変数がそれぞれ1つの方程式にまとめられることです。実際今定義した記号を用いれば、
\boldsymbol{\hat{y}}=\boldsymbol{X}\boldsymbol{\beta} \tag8
と、とてもシンプルな形になりました!
あとは、これを$\boldsymbol{\beta}$について最適化するだけです!
幾何学的に速攻で解く
またまたあらためて、単回帰の式を示します。
\hat{y_i}=ax_i+b
この式には未知変数が$a,b$と2つあります。
これが何を意味するのかというと、幾何学的には推定値$\hat{y_i}$は2次元平面上の1点を表すベクトルとして表せるということです。
一方、$y_i$はどうでしょうか。$y_i$が回帰直線上に乗らないことから分かるように、これは2次元平面の外にあります。これを図に書くと以下のようになります。
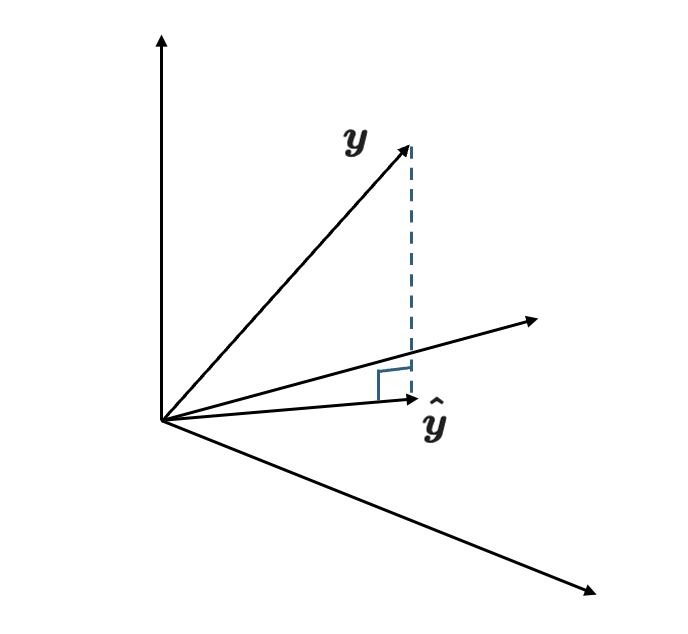
そして、最適な$\boldsymbol{\beta}$を求めるということは、この$\hat{y_i}$が$y_i$に最も近いようなベクトルにすれば良いということです。つまり式で言えば、
argmin_{\boldsymbol{\hat{\beta}}}\|\boldsymbol{y}-\boldsymbol{\hat{y}}\|^2 \tag9
であり、二乗誤差を最小化する最小二乗法での定式化と一致します。
では、式$(9)$を達成する$\boldsymbol{\hat{y}}$はどうなるでしょうか。
そのような$\boldsymbol{\hat{y}}$は、図の通り$\boldsymbol{y}$の2次元平面への射影となります。したがって、$\boldsymbol{y}-\boldsymbol{\hat{y}}$と$\boldsymbol{y}$は直交します。
以上より、
\boldsymbol{y}^T(\boldsymbol{y}-\boldsymbol{\hat{y}})=0\tag{10}
式$(10)$に式$(8)$を代入して解けば、
\boldsymbol{\hat{\beta}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\tag{11}
が得られます!
ただし、式$(11)$中の逆行列が存在しない場合があるので注意が必要です(=>正則化が必要になります)。