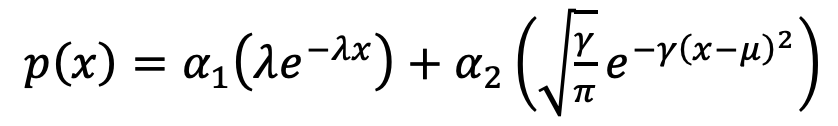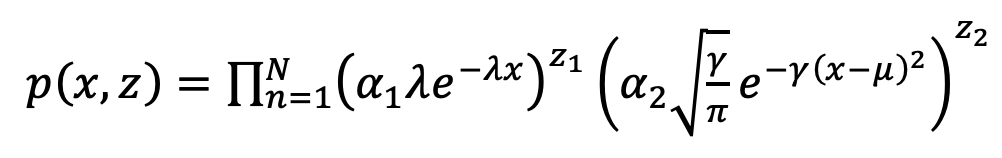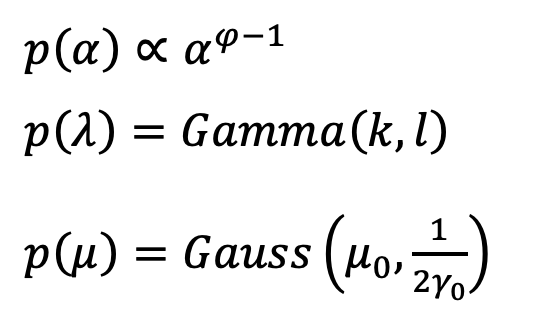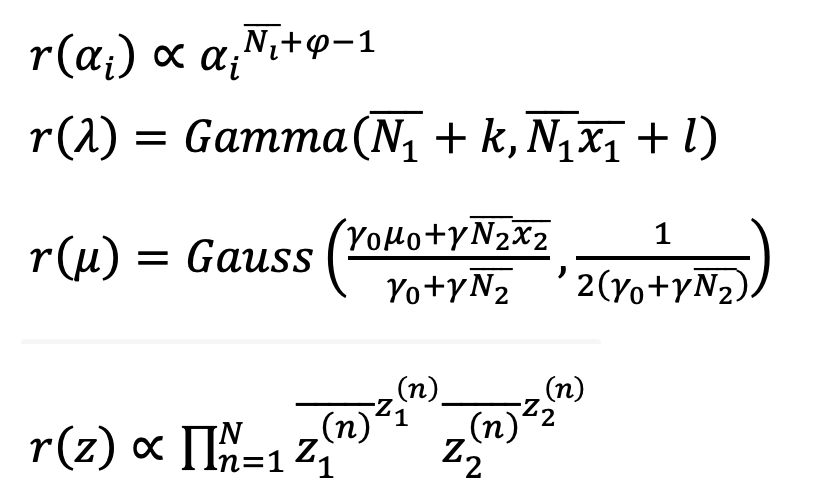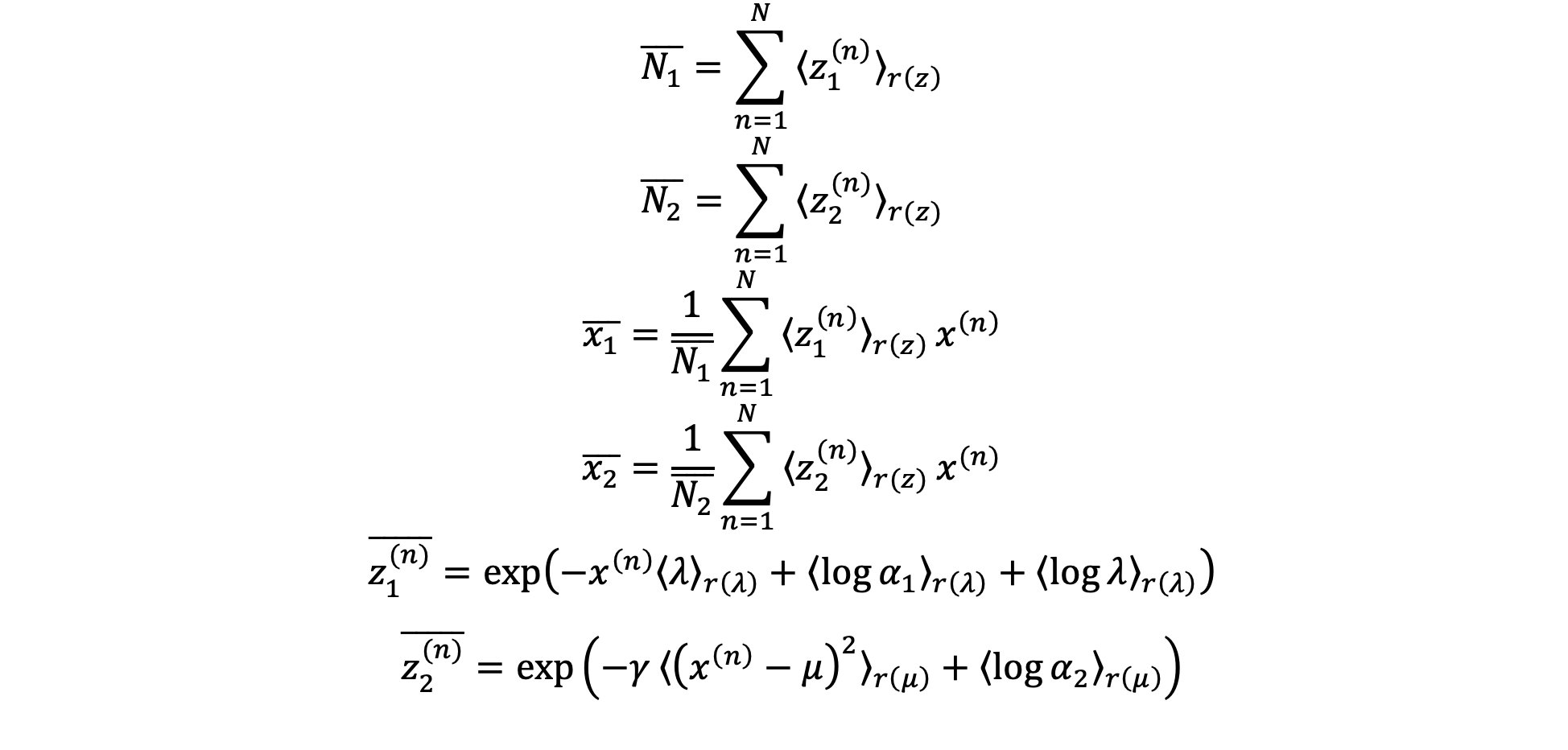ガウス分布と指数分布の混合分布
1次元のガウス分布と指数分布の混合分布は以下の式で表される
ここに潜在変数$z_i$を導入すると
と積の形でかけ、尤度計算がしやすい
混合分布の事後分布
事前分布を以下のように定める
このとき、変分ベイズの事後分布は
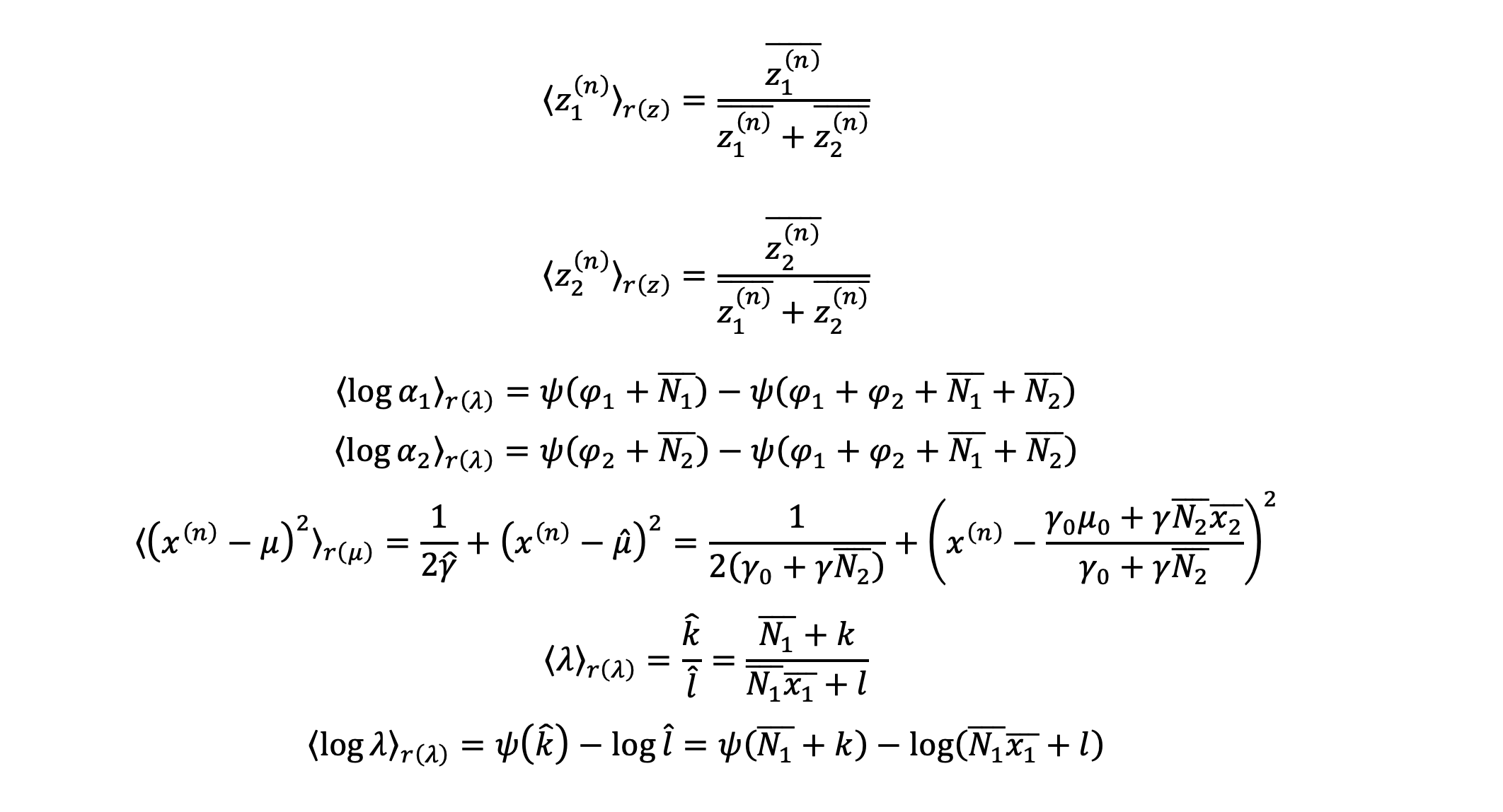
また、各パラメータについて、以下の式が成り立つ。
各期待値は以下のように表せる。
変分ベイズ学習を実践
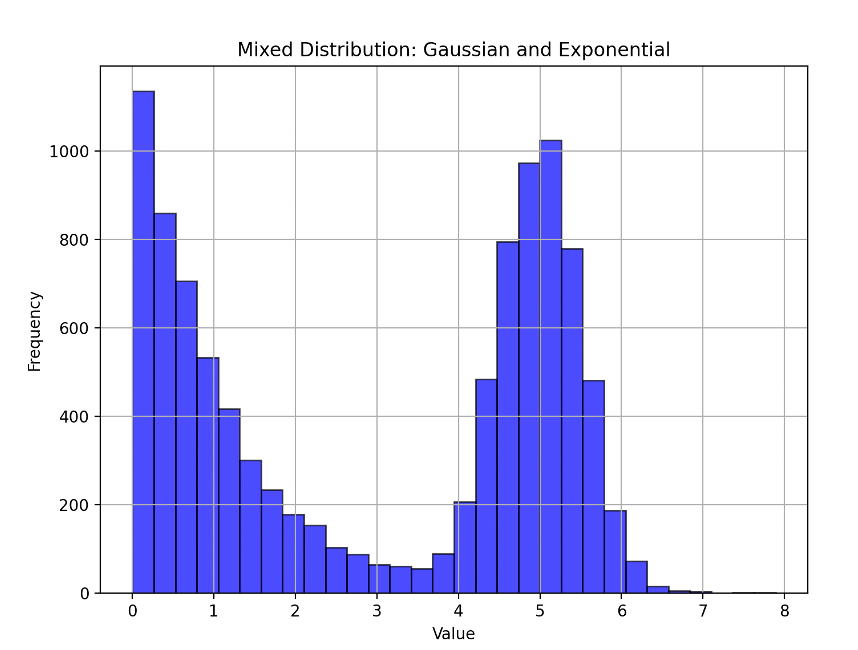
$λ=1$の指数分布と$μ=5$のガウス分布を1:1の割合で混合した分布をpythonで発生させる(ガウス分布の分散既知とする)。
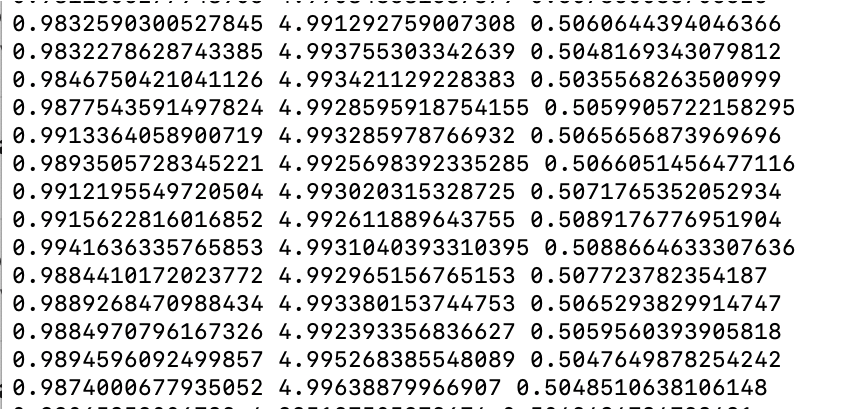
この分布を変分ベイズ推定すると以下のような結果が得られる。
左から順に
$λ$、 $μ$、指数分布からサンプリングされる割合
となっており分布のパラメータを学習できていることが窺える
プログラム
import numpy as np
import math
import matplotlib.pyplot as plt
import scipy.special as sp
def F_Ni(zi_rz):
s = 0
for z in zi_rz:
s += z
return s
def F_xi(Ni,zi_rz,x):
s = 0
for i in range(len(x)):
s += zi_rz[i]*x[i]
return s
def F_z1(x,E_lambda,E_log_alpha_1,E_log_lambda):
N = len(x)
res = [0 for i in range(N)]
for i in range(N):
res[i] = math.exp(-x[i]*E_lambda+E_log_alpha_1+E_log_lambda)
return res
def F_z2(gamma_const,E_mom2,E_log_alpha_2):
N = len(E_mom2)
res = [0 for i in range(N)]
for i in range(N):
res[i] = math.exp(-gamma_const*E_mom2[i]+E_log_alpha_2)
return res
def F_z1_rz(z1,z2):
N = len(z1)
res = [0 for i in range(N)]
for i in range(N):
res[i] = z1[i]/(z1[i]+z2[i])
return res
def F_z2_rz(z1,z2):
N = len(z1)
res = [0 for i in range(N)]
for i in range(N):
res[i] = z2[i]/(z1[i]+z2[i])
return res
def F_E_log_alpha_1(phai1_after_tmp,phai2_after_tmp,N1,N2):
return sp.digamma(phai1_after_tmp+N1)-sp.digamma(phai1_after_tmp+phai2_after_tmp+N1+N2)
def F_E_log_alpha_2(phai1_after_tmp,phai2_after_tmp,N1,N2):
return sp.digamma(phai2_after_tmp+N2)-sp.digamma(phai1_after_tmp+phai2_after_tmp+N1+N2)
def F_E_mom2(gamma_after,x,mu_after):
N = len(x)
res = [0 for i in range(N)]
for i in range(N):
res[i] = 1/(2*gamma_after) + (x[i]-mu_after)**2
return res
def F_E_lambda(k_after,l_after):
return k_after/l_after
def F_E_log_lambda(k_after,l_after):
return sp.digamma(k_after)-math.log(l_after)
#ベイズ更新
def F_k_after(N1,k):
return N1+k
def F_l_after(N1,x1,l):
return x1+l
def F_mu0_after(gamma0,mu0,gamma_const,N2,x2):
return (gamma0*mu0+gamma_const*x2)/(gamma0+gamma_const*N2)
def F_gamma0_after(gamma0,gamma_const,N2):
return gamma0+gamma_const*N2
def solver(batch,x,params,gamma_const):
#params = [k_after,l_after,mu0_after,gamma0_after]
k_after = params[0]
l_after = params[1]
mu0_after = params[2]
gamma0_after = params[3]
phai1_after = params[4]
phai2_after = params[5]
k_after_tmp = params[0]
l_after_tmp = params[1]
mu0_after_tmp = params[2]
gamma0_after_tmp = params[3]
phai1_after_tmp = params[4]
phai2_after_tmp = params[5]
E_lambda = 1
E_log_alpha_1 = -1
E_log_alpha_2 = -1
E_log_lambda = 0
E_lambda_before = 0
E_log_alpha_1_before = -1
E_log_alpha_2_before = -1
E_log_lambda_before = 0
z1 = [ 0 for i in range(batch)]
z2 = [ 0 for i in range(batch)]
E_mom2 = [ 1 for i in range(batch)]
E_mom2_before = [ 0 for i in range(batch)]
eps = 0.00001
f1 = True
f2 = True
f3 = True
f4 = True
f5 = True
while f1 or f2 or f3 or f4 or f5:
f5 = False
z1 = F_z1(x,E_lambda,E_log_alpha_1,E_log_lambda)
z2 = F_z2(gamma_const,E_mom2,E_log_alpha_2)
z1_rz = F_z1_rz(z1,z2)
z2_rz = F_z2_rz(z1,z2)
N1 = F_Ni(z1_rz)
N2 = F_Ni(z2_rz)
x1 = F_xi(N1,z1_rz,x)
x2 = F_xi(N2,z2_rz,x)
E_log_alpha_1 = F_E_log_alpha_1(phai1_after_tmp,phai2_after_tmp,N1,N2)
E_log_alpha_2 = F_E_log_alpha_2(phai1_after_tmp,phai2_after_tmp,N1,N2)
k_after_tmp = F_k_after(N1,k_after_tmp)
l_after_tmp = F_l_after(N1,x1,l_after_tmp)
mu0_after_tmp = F_mu0_after(gamma0_after_tmp,mu0_after_tmp,gamma_const,N2,x2)
gamma0_after_tmp = F_gamma0_after(gamma0_after_tmp,gamma_const,N2)
E_mom2 = F_E_mom2(gamma0_after_tmp,x,mu0_after_tmp)
#print(N2)
#input()
E_lambda = F_E_lambda(k_after_tmp,l_after_tmp)
E_log_lambda = F_E_log_lambda(k_after_tmp,l_after_tmp)
f1 = (abs(E_lambda - E_lambda_before) > eps)
f2 = (abs(E_log_alpha_1 - E_log_alpha_1_before) > eps)
f3 = (abs(E_log_alpha_2 - E_log_alpha_2_before) > eps)
f4 = (abs(E_log_lambda - E_log_lambda_before) > eps)
#print(f1,f4,f5)
for i in range(batch):
f5 += (abs(E_mom2[i] - E_mom2_before[i]) > eps)
E_lambda_before = E_lambda
E_log_alpha_1_before = E_log_alpha_1
E_log_alpha_2_before = E_log_alpha_2
E_log_lambda_before = E_log_lambda
for i in range(batch):
E_mom2_before[i] = E_mom2[i]
k_after = F_k_after(N1,k_after)
l_after = F_l_after(N1,x1,l_after)
mu0_after = F_mu0_after(gamma0_after,mu0_after,gamma_const,N2,x2)
gamma0_after = F_gamma0_after(gamma0_after,gamma_const,N2)
return [k_after,l_after,mu0_after,gamma0_after,N1+phai1_after,N2+phai2_after]
def execute_analysis(mixed_samples):
k_after = 1
l_after = 1
mu0_after = 0
gamma0_after = 1
gamma_const = 2
phai1 = 1
phai2 = 1
params = [k_after,l_after,mu0_after,gamma0_after,phai1,phai2]
batch = 10
x = [ 0 for i in range(batch)]
for i in range(int(len(mixed_samples)/batch)):
x = [mixed_samples[batch*i+j] for j in range(batch)]
params = solver(batch,x,params,gamma_const)
#params[0] /= 100
#params[1] /= 100
print(params[0]/params[1],params[2],(params[4]-1)/(params[4]+params[5]-2))
# パラメータ設定
mu = 5 # ガウス分布の平均
sigma = 0.5 # ガウス分布の標準偏差
lambda_exp = 1 # 指数分布のパラメータ (レート λ)
# ガウス分布と指数分布の混合割合 (0.5はそれぞれ半分ずつ)
mixing_ratio = 0.5
# 乱数の個数
num_samples = 10000
# どちらの分布からサンプルするかを決めるフラグを生成 (0: ガウス, 1: 指数)
flags = np.random.choice([0, 1], size=num_samples, p=[mixing_ratio, 1 - mixing_ratio])
# ガウス分布からのサンプル
gaussian_samples = np.random.normal(mu, sigma, num_samples)
# 指数分布からのサンプル
exponential_samples = np.random.exponential(1 / lambda_exp, num_samples)
# フラグに基づいて最終的なサンプルを決定
mixed_samples = np.where(flags == 0, gaussian_samples, exponential_samples)
# ヒストグラムを描画
plt.figure(figsize=(8, 6))
plt.hist(mixed_samples, bins=30, alpha=0.7, color='b', edgecolor='black')
plt.title('Mixed Distribution: Gaussian and Exponential')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.grid(True)
# グラフ表示
plt.show()
execute_analysis(mixed_samples)