仕事で数理計画(数理最適化)を触ることがちょくちょくある。
職場では、ライセンス費年間3ケタ万円とかのツール&ソルバを使えるが、自主学習用にはとてもじゃないが用意できないので、Googleのオープンソース数理最適化ツールが使えるか試してみる。
環境整備
インストール
公式ページに環境別のインストール方法が載っている。
今回は、会社の環境と同じくWindows + Python3.7を前提にする。
公式ページに注意書きがあるが、64bitアーキテクチャしかサポートしていないらしい。
Note: OR-Tools only supports the x86_64 (also known as amd64) architecture.
今どきは大抵問題ないだろうが、大企業とかだと組織運営的に環境移行が遅くて、まだ残っていることもありそうなので注意する。
前提で問題なければ、pipとかでインストールするだけ。
pip install ortools
公式ページでは、--userオプションついているがその辺はお好みで。
適当に問題解いてみる
まるっきり一緒ではないが、業務でやったスケジュール作成に近いものをやってみる。
1つのリソースに対して複数の仕事を時間を守りながら順番に割り付ける問題を想定。
一般的には1機械問題というらしい。
問題の概要
1つのリソースに対して、$N$個の仕事を割り付ける。仕事にはそれぞれ、"作業可能時間"が設定されていて、各仕事は作業の開始~終了を"作業可能時間"内に収めないといけない。
また、リソースにも使用時間の制限があり、仕事の割り当てはリソースの使用可能時間内にしなければならない。
なお、$N$個の仕事がすべて割り付けられれば、リソースの使用時間を最短にする必要はない。
代数定義
| 代数 | カテゴリ | 内容 |
|---|---|---|
| $N$ | 集合 | 割り付け対象にする仕事の集合 |
| $n$ | 添え字 | 集合$N$の添え字 |
| $n_1$ | 添え字 | 集合$N$の添え字.順序決め組合せ用 |
| $n_2$ | 添え字 | 集合$N$の添え字.順序決め組合せ用 |
| $s_n$ | 変数 | 仕事$n$の作業開始時刻 |
| $lim\_min$ | 定数 | リソースの使用可能時間の下限時刻 |
| $lim\_max$ | 定数 | リソースの使用可能時間の上限時刻 |
| $lim\_s_n$ | 定数 | 仕事$n$の作業可能時間の下限時刻 |
| $lim\_t_n$ | 定数 | 仕事$n$の作業可能時間の上限時刻 |
| $\nu_n$ | 定数 | 仕事$n$の作業時間 |
| $x_{n_1,n_2}$ | 変数 | 仕事$n_1$と$n_2$の順序設定フラグ |
| $M$ | 定数 | 適当な大きい値の実数 |
制約の定義
-
仕事$n$の作業開始時刻は、その仕事$n$に設定された作業可能時間及び、リソースの使用可能時間の下限時刻以降でなければならない。
$$
\begin{eqnarray}
s_n &\ge& lim\_s_n \qquad & \forall n \in N \\
s_n &\ge& lim\_min \qquad & \forall n \in N
\end{eqnarray}
$$ -
仕事$n$の作業完了時刻は、その仕事$n$に設定された作業可能時間及び、リソースの使用可能時間の上限時刻以前でなければならない。
$$
\begin{eqnarray}
lim\_t_n &\ge& s_n + \nu_n \qquad & \forall n \in N \\
lim\_max &\ge& s_n + \nu_n \qquad & \forall n \in N
\end{eqnarray}
$$ -
リソースに対して、同時に複数の仕事を割り当てることはできない。
$$
\begin{eqnarray}
\begin{array}{l}
s_{n_2} &\gt& s_{n_1} + \nu_{n_1} - M(1-x_{n_1,n_2}) \\
s_{n_1} &\gt& s_{n_2} + \nu_{n_2} - M \cdot x_{n_1,n_2}
\end{array}
\qquad n_1 \neq n_2, \forall n_1 \in N, \forall n_2 \in N
\end{eqnarray}
$$
目的関数の定義
制約を満たしている満足解を得られれば良いので、特に設定しない。
Pythonでの実装
モジュールのインポート
ortoolsをインポートする。今回はMIP(混合整数最適化問題)なので、公式ページのここを参考にする。
from ortools.linear_solver import pywraplp
あとは、今回の例題用にいくつかインポートする。時刻を足し引きするのでdatetime.timedeltaを、順序設定時に仕事の数から組合せを算出するのにitertools.combnationsを使う。
pandasは標準ライブラリではないが、仕事毎のパラメータ設定等の視認性と利便性で使っている。管理できればpandasを使わなくてもいい。
from datetime import timedelta as td
import pandas as pd
from itertools import combinations
ソルバのインスタンスを生成
これも、公式ページを参考に設定する。今回はMIP(混合整数最適化問題)なので、pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMINGであるが、問題によってソルバを切り替える形みたい。
solver = pywraplp.Solver("MIP", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
データを定義
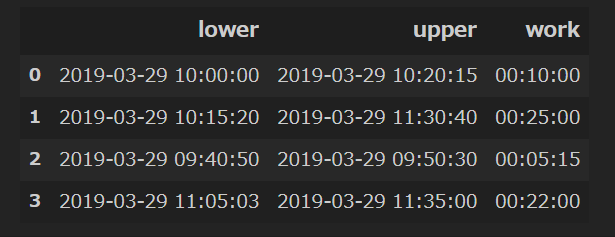
適当に4つの仕事を定義する。
作業可能時間(lower, upper)と作業に要する時間(work)を仕事毎に設定する、
実務だと仕事の要求に紐づいているのだろうが、今回は例題なので自分で適当に決めた。
jobs = pd.DataFrame(columns=["lower", "upper", "work"])
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:00:00"), pd.to_datetime("10:20:15"), td(minutes=10)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:15:20"), pd.to_datetime("11:30:40"), td(minutes=25)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("09:40:50"), pd.to_datetime("9:50:30"), td(minutes=5, seconds=15)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("11:05:03"), pd.to_datetime("11:35:00"), td(minutes=22)],
index=jobs.columns
), ignore_index=True
)
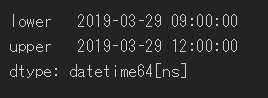
リソースの使用可能時間(lower, upper)を定義する。
これも適当に自分で決めた。実務だと始業~終業の時間とかになるはず。
resource = pd.Series({"lower": pd.to_datetime("9:00:00"), "upper": pd.to_datetime("12:00:00")})
問題の実装
- 下準備
問題上は時刻を基準値からの秒数で扱う必要があるので、時刻系をすべてfloatに変換する。
何らかでtimedeltaに変換してtotal_seconds()メソッドで秒数を取り出していく。
今回はpandasを使っているので、applymap()やmap()メソッドで一気に変換する。
def dt2f(x):
return (x - pd.to_datetime("0:0:0", format="%H:%M:%S")).total_seconds()
def td2f(x):
return x.total_seconds()
jobs[["lower", "upper"]] = jobs[["lower", "upper"]].applymap(dt2f)
jobs["work"] = jobs["work"].map(td2f)
resource = resource.map(dt2f)
- 各仕事の変数と制約を設定する。
各仕事の作業開始時刻を設定する変数sは、時刻秒数を連続的に推移させるので、連続数の変数インスタンスをsolver.NumVar()で作成する。
s[n] = solver.NumVar(resource["lower"], resource["upper"], "s{}".format(n))
solver.NumVar()には、第一引数に作成する変数の下限値、第二引数に上限値、第三引数に変数名を指定する。
今回は全仕事で共通の上下限値である、リソースの使用可能時間を設定したが、変数作成時点では上下限無限にして制約で後付けしてもいい。
各仕事sには、仕事毎の作業可能時間の上下限もあるので、solver.Constraint()で制約を作成して、SetCoefficient()メソッドで付加する。
constraints.append(solver.Constraint(v["lower"], v["upper"] - v["work"]))
constraints[-1].SetCoefficient(s[n], 1)
solver.Constraint()は、第一引数に制約式の可変範囲下限値、第二引数に上限値を指定する。
制約のインスタンスを作成した後、SetCoefficient()メソッドで対応する変数と係数を設定する。
SetCoefficient()メソッドは第一引数に対応する変数のインスタンス、第二引数にその変数にかかる係数を設定する。
このような制約を作ってから、変数と係数を設定する作りなので、事前に制約式を定数項と変数項でまとめておくとやりやすい。
ここまでの流れを一連で書くとこのようになる。
# 制約インスタンス用のリストを定義
constraints = list()
# 作業開始時刻の変数を定義
s = dict()
for n, v in jobs.iterrows():
# リソースの使用可能時間幅で変数を定義
s[n] = solver.NumVar(resource["lower"], resource["upper"], "s{}".format(n))
# 仕事毎の作業可能時間の制限を付加する
constraints.append(solver.Constraint(v["lower"], v["upper"] - v["work"]))
constraints[-1].SetCoefficient(s[n], 1)
- 順序設定の変数と制約を設定する。
作業開始時刻の変数sと同様に、順序設定の変数xとそれの制約を作成する。
制約中にsを使うので、sを設定後に設定する。
n1とn2の組合わせなので、itertools.combinations()で仕事jobsのイテレータから2つの組合わせを作成してイテレーションする。
for (n1, v1), (n2, v2) in combinations(jobs.iterrows(), 2):
xは仕事n1がn2の前に作業完了するか否かを1,0で表現するので、solver.IntVar()で整数変数のインスタンスとして作成する。
引数はsolver.NumVar()と同様。
x[(n1, n2)] = solver.IntVar(0, 1, "x[{},{}]".format(n1, n2))
順序に基づき後攻の作業開始時刻を、先行の作業完了時刻以降に制限する制約を作る。
順序の設定によって、2つの相反する制約を排他的に切り替えるため、"適当な大きい値の実数"Mを作成する。
「適当な大きい値ってどれくらい?」となるが、無効にする側の作業開始時刻をリソースの使用可能時間下限以下にすれば、実質無効化になるのでリソースの使用可能時間幅をMとすれば最悪値の時でも十分大きい値として機能する。
M = resource["upper"] - resource["lower"]
順序の制約を設定する。
基本的には作業開始時刻の変数sと同様だが、こちらは関連する変数が複数あるので、式を定数項と変数項に整理して、各変数の符号・係数を明確にした上で設定する。
$$
\begin{eqnarray}
s_{n_2} &\gt& s_{n_1} + \nu_{n_1} - M(1-x_{n_1,n_2}) \\
s_{n_2} - s_{n_1} - M \cdot x_{n_1,n_2} &\gt& \nu_{n_1} - M
\end{eqnarray}
$$
$$
\begin{eqnarray}
s_{n_1} &\gt& s_{n_2} + \nu_{n_2} - M \cdot x_{n_1,n_2} \\
s_{n_1} - s_{n_2} + M \cdot x_{n_1,n_2} &\gt& \nu_{n_2}
\end{eqnarray}
$$
constraints.append(solver.Constraint(v1["work"] - M, solver.infinity()))
constraints[-1].SetCoefficient(s[n2], 1)
constraints[-1].SetCoefficient(s[n1], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], -M)
constraints.append(solver.Constraint(v2["work"], solver.infinity()))
constraints[-1].SetCoefficient(s[n1], 1)
constraints[-1].SetCoefficient(s[n2], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], M)
ここまでの流れを一連で書くと以下のようになる。
# 適当な大きな実数を定義
M = resource["upper"] - resource["lower"]
# 順序設定フラグの変数を定義
x = dict()
for (n1, v1), (n2, v2) in combinations(jobs.iterrows(), 2):
# 順序設定変数を定義
x[(n1, n2)] = solver.IntVar(0, 1, "x[{},{}]".format(n1, n2))
# 順序に基づく作業開始時刻の設定制限を付加する
constraints.append(solver.Constraint(v1["work"] - M, solver.infinity()))
constraints[-1].SetCoefficient(s[n2], 1)
constraints[-1].SetCoefficient(s[n1], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], -M)
constraints.append(solver.Constraint(v2["work"], solver.infinity()))
constraints[-1].SetCoefficient(s[n1], 1)
constraints[-1].SetCoefficient(s[n2], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], M)
- 求解
今回、目的関数はないので、そのまま求解する。
solver.Solve()で計算が実行され、結果のステータスが戻り値で得られる。
ソルバのインスタンスにステータス判定用のプロパティを持っているみたいだが、公式ページ中でクラスのリファレンスなどを見つけられなかったので、とりあえずOPTIMALか否かで処理分けしてみる。
概要として、変数の数・制約の数および求解結果のコスト関数の値を表示している。
この辺は、公式ページに載っているサンプルそのまま。
result_status = solver.Solve()
if result_status == solver.OPTIMAL:
print("Number of variables = {}".format(solver.NumVariables()))
print("Number of constraints = {}".format(solver.NumConstraints()))
print("Optimal objective value = {}".format(solver.Objective().Value()))
print()
- 各仕事の作業開始時刻を取得
求解が終わった作業開始時刻を取り出す。後処理のためにpandas.DataFrameに保存する。
求解で決まっているのは作業開始時刻だけなので、作業完了時刻は作業開始時刻から各仕事の作業時間をオフセットして決定する。
sol = pd.DataFrame(index=jobs.index, columns=["start", "complete"])
for k, v in s.items():
sol.at[k, "start"] = v.solution_value()
sol.at[k, "complete"] = v.solution_value() + jobs.at[k, "work"]
求解結果だけだと、すべて起点からの秒数になっていて一目でわからないので、datatimeに変換しておく。
def f2dt(x):
return pd.to_datetime("0:0:0", format="%H:%M:%S") + td(seconds=x)
sol = sol.applymap(f2dt)
最後に、作業開始時刻をキーにソートする。
sol.sort_values("start", inplace=True)
- ここまでのすべてを一連にする。
from ortools.linear_solver import pywraplp
from datetime import timedelta as td
import pandas as pd
from itertools import combinations
solver = pywraplp.Solver("MIP", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# 仕事を定義
jobs = pd.DataFrame(columns=["lower", "upper", "work"])
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:00:00"), pd.to_datetime("10:20:15"), td(minutes=10)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:15:20"), pd.to_datetime("11:30:40"), td(minutes=25)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("09:40:50"), pd.to_datetime("9:50:30"), td(minutes=5, seconds=15)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("11:05:03"), pd.to_datetime("11:35:00"), td(minutes=22)],
index=jobs.columns
), ignore_index=True
)
print(jobs)
print()
resource = pd.Series({"lower": pd.to_datetime("9:00:00"), "upper": pd.to_datetime("12:00:00")})
print(resource)
print()
# 仕事の時刻系をfloatにする
def dt2f(x):
return (x - pd.to_datetime("0:0:0", format="%H:%M:%S")).total_seconds()
def td2f(x):
return x.total_seconds()
jobs[["lower", "upper"]] = jobs[["lower", "upper"]].applymap(dt2f)
jobs["work"] = jobs["work"].map(td2f)
resource = resource.map(dt2f)
# 制約インスタンス用のリストを定義
constraints = list()
# 作業開始時刻の変数を定義
s = dict()
for n, v in jobs.iterrows():
# リソースの使用可能時間幅で変数を定義
s[n] = solver.NumVar(resource["lower"], resource["upper"], "s{}".format(n))
# 仕事毎の作業可能時間の制限を付加する
constraints.append(solver.Constraint(v["lower"], v["upper"] - v["work"]))
constraints[-1].SetCoefficient(s[n], 1)
# 適当な大きな実数を定義
M = resource["upper"] - resource["lower"]
# 順序設定フラグの変数を定義
x = dict()
for (n1, v1), (n2, v2) in combinations(jobs.iterrows(), 2):
# 順序設定変数を定義
x[(n1, n2)] = solver.IntVar(0, 1, "x[{},{}]".format(n1, n2))
# 順序に基づく作業開始時刻の設定制限を付加する
constraints.append(solver.Constraint(v1["work"] - M, solver.infinity()))
constraints[-1].SetCoefficient(s[n2], 1)
constraints[-1].SetCoefficient(s[n1], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], -M)
constraints.append(solver.Constraint(v2["work"], solver.infinity()))
constraints[-1].SetCoefficient(s[n1], 1)
constraints[-1].SetCoefficient(s[n2], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], M)
# 求解
result_status = solver.Solve()
if result_status == solver.OPTIMAL:
print("Number of variables = {}".format(solver.NumVariables()))
print("Number of constraints = {}".format(solver.NumConstraints()))
print("Optimal objective value = {}".format(solver.Objective().Value()))
print()
# 求解結果の作業開始時刻を読み込み
sol = pd.DataFrame(index=jobs.index, columns=["start", "complete"])
for k, v in s.items():
sol.at[k, "start"] = v.solution_value()
sol.at[k, "complete"] = v.solution_value() + jobs.at[k, "work"]
# floatを時刻系に変換
def f2dt(x):
return pd.to_datetime("0:0:0", format="%H:%M:%S") + td(seconds=x)
sol = sol.applymap(f2dt)
# 作業開始順にソート
sol.sort_values("start", inplace=True)
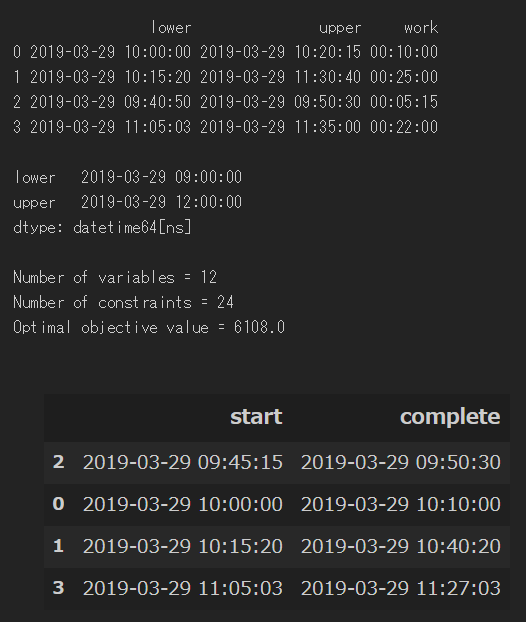
sol
ちゃんと制限を守った順序になっている。目的関数未設定なので、仕事同士の間隔が空いている。
目的関数の設定
今回の問題の趣旨ではないが、今後汎用的に使うなら目的関数の設定もできないといけないでしょう。
ということで、今回の問題で仕事の作業時間を最短にする目的を付加してみる。
補助変数の追加
各仕事中の作業開始時刻の最短値及び、作業完了時刻の最長値を補助変数として、$s\_min$・$t\_max$に設定する。
$$
\begin{eqnarray}
s\_min &\le& s_n \qquad &\forall n \in N \\
s_n + \nu_n &\le& t\_max \qquad &\forall n \in N
\end{eqnarray}
$$
コスト関数の作成
最長時刻と最短時刻の差分を最小化するようにコスト関数を定義する。
$$
Minimize \qquad t\_max - s\_min
$$
実装部の改造
補助変数を追加で作って、各仕事の作業開始時刻設定ループの中で制約を付加する。
# 補助変数を作成
s_min = solver.NumVar(resource["lower"], resource["upper"], "s_min")
t_max = solver.NumVar(resource["lower"], resource["upper"], "t_max")
# 制約インスタンス用のリストを定義
constraints = list()
# 作業開始時刻の変数を定義
s = dict()
for n, v in jobs.iterrows():
# リソースの使用可能時間幅で変数を定義
s[n] = solver.NumVar(resource["lower"], resource["upper"], "s{}".format(n))
# 仕事毎の作業可能時間の制限を付加する
constraints.append(solver.Constraint(v["lower"], v["upper"] - v["work"]))
constraints[-1].SetCoefficient(s[n], 1)
# 補助変数に対応する制約作成
constraints.append(solver.Constraint(0.0, solver.infinity()))
constraints[-1].SetCoefficient(s[n], 1)
constraints[-1].SetCoefficient(s_min, -1)
constraints.append(solver.Constraint(v["work"], solver.infinity()))
constraints[-1].SetCoefficient(t_max, 1)
constraints[-1].SetCoefficient(s[n], -1)
目的関数のインスタンスを作成して設定する。
基本的に制約式の設定の仕方と同じで、違いはインスタンスの生成時に指定するものがないことと、最大化問題か最小化問題かの設定があるくらい。
もし、最大化問題にしたい時はobjective.SetMaxmization()にすればいいが、各項の符号反転でも対応できるので覚えてなくてもよさそう。
objective = solver.Objective()
objective.SetCoefficient(t_max, 1)
objective.SetCoefficient(s_min, -1)
objective.SetMinimization()
以上を反映させたプログラムが下記。
from ortools.linear_solver import pywraplp
from datetime import timedelta as td
import pandas as pd
from itertools import combinations
solver = pywraplp.Solver("MIP", pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# 仕事を定義
jobs = pd.DataFrame(columns=["lower", "upper", "work"])
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:00:00"), pd.to_datetime("10:20:15"), td(minutes=10)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("10:15:20"), pd.to_datetime("11:30:40"), td(minutes=25)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("09:40:50"), pd.to_datetime("9:50:30"), td(minutes=5, seconds=15)],
index=jobs.columns
), ignore_index=True
)
jobs = jobs.append(
pd.Series(
[pd.to_datetime("11:05:03"), pd.to_datetime("11:35:00"), td(minutes=22)],
index=jobs.columns
), ignore_index=True
)
print(jobs)
print()
resource = pd.Series({"lower": pd.to_datetime("9:00:00"), "upper": pd.to_datetime("12:00:00")})
print(resource)
print()
# 仕事の時刻系をfloatにする
def dt2f(x):
return (x - pd.to_datetime("0:0:0", format="%H:%M:%S")).total_seconds()
def td2f(x):
return x.total_seconds()
jobs[["lower", "upper"]] = jobs[["lower", "upper"]].applymap(dt2f)
jobs["work"] = jobs["work"].map(td2f)
resource = resource.map(dt2f)
# 補助変数を作成
s_min = solver.NumVar(resource["lower"], resource["upper"], "s_min")
t_max = solver.NumVar(resource["lower"], resource["upper"], "t_max")
# 制約インスタンス用のリストを定義
constraints = list()
# 作業開始時刻の変数を定義
s = dict()
for n, v in jobs.iterrows():
# リソースの使用可能時間幅で変数を定義
s[n] = solver.NumVar(resource["lower"], resource["upper"], "s{}".format(n))
# 仕事毎の作業可能時間の制限を付加する
constraints.append(solver.Constraint(v["lower"], v["upper"] - v["work"]))
constraints[-1].SetCoefficient(s[n], 1)
# 補助変数に対応する制約作成
constraints.append(solver.Constraint(0.0, solver.infinity()))
constraints[-1].SetCoefficient(s[n], 1)
constraints[-1].SetCoefficient(s_min, -1)
constraints.append(solver.Constraint(v["work"], solver.infinity()))
constraints[-1].SetCoefficient(t_max, 1)
constraints[-1].SetCoefficient(s[n], -1)
# 適当な大きな実数を定義
M = resource["upper"] - resource["lower"]
# 順序設定フラグの変数を定義
x = dict()
for (n1, v1), (n2, v2) in combinations(jobs.iterrows(), 2):
# 順序設定変数を定義
x[(n1, n2)] = solver.IntVar(0, 1, "x[{},{}]".format(n1, n2))
# 順序に基づく作業開始時刻の設定制限を付加する
constraints.append(solver.Constraint(v1["work"] - M, solver.infinity()))
constraints[-1].SetCoefficient(s[n2], 1)
constraints[-1].SetCoefficient(s[n1], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], -M)
constraints.append(solver.Constraint(v2["work"], solver.infinity()))
constraints[-1].SetCoefficient(s[n1], 1)
constraints[-1].SetCoefficient(s[n2], -1)
constraints[-1].SetCoefficient(x[(n1, n2)], M)
# 目的関数の設定
objective = solver.Objective()
objective.SetCoefficient(t_max, 1)
objective.SetCoefficient(s_min, -1)
objective.SetMinimization()
# 求解
result_status = solver.Solve()
if result_status == solver.OPTIMAL:
print("Number of variables = {}".format(solver.NumVariables()))
print("Number of constraints = {}".format(solver.NumConstraints()))
print("Optimal objective value = {}".format(solver.Objective().Value()))
print()
# 求解結果の作業開始時刻を読み込み
sol = pd.DataFrame(index=jobs.index, columns=["start", "complete"])
for k, v in s.items():
sol.at[k, "start"] = v.solution_value()
sol.at[k, "complete"] = v.solution_value() + jobs.at[k, "work"]
# floatを時刻系に変換
def f2dt(x):
return pd.to_datetime("0:0:0", format="%H:%M:%S") + td(seconds=x)
sol = sol.applymap(f2dt)
# 作業開始順にソート
sol.sort_values("start", inplace=True)
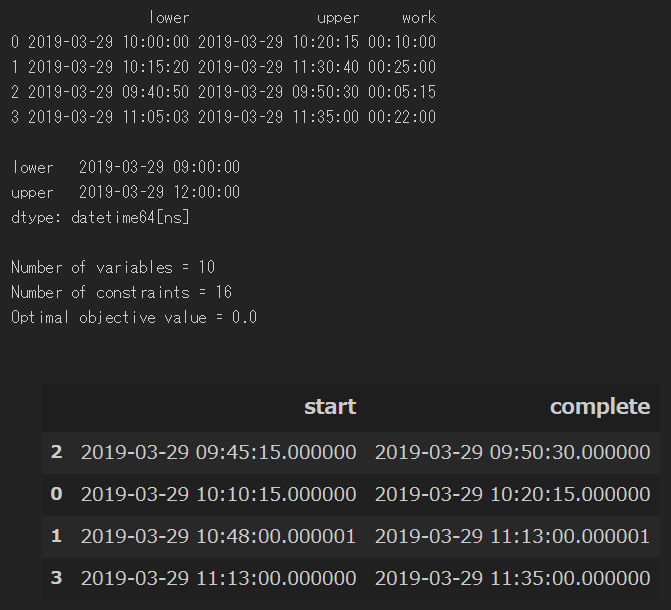
sol
例として設定したデータの値が微妙だったせいでわかりにくいが、リソースの所要時間は最小化されている。
最後に
大きい問題はやったことがないが、ちょっとした問題には十分使える。
デフォルトでつくソルバはCBC-Coinというオープンソースのものらしいので、PuLPとかほかのライブラリと同じような性能だと思われる。
変数や制約をインスタンスとして作成してそれぞれ設定するやり方は好みが分かれそうだが、個人的には結構好き。
今回はMIPを解いたが、いくつかヒューリスティックサーチのアルゴリズムも持っていたりするみたいなので、そのうち使ってみたい。
「逐次処理でもできるんだけど、面倒だから式起こしちゃえ!」みたいなものから徐々に使って行ってみようかなと。