ABC129で初めてC問題を解いた(python)

弱小Pythonistaなので、一度もAtCoderに出場したことはないのですが、
そろそろ戦わないとと奮起し、AtCoderに取り組んでみた。

A,B問題は簡単なのでどうでもいい
僕からするとC問題は難しい

そこでAtCoder129のC問題に取り組んでみた。

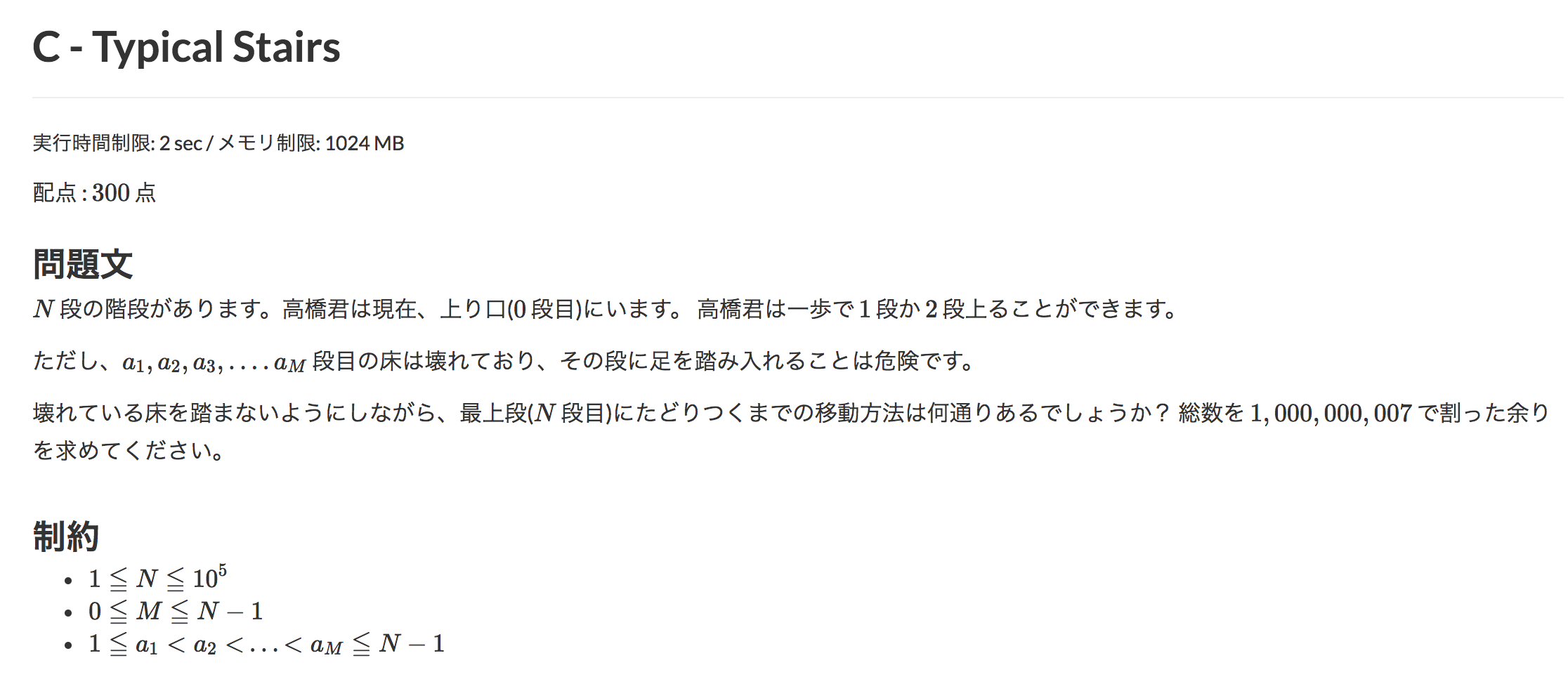
#AtCoder129のC問題

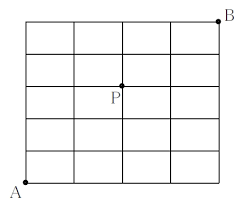
####なるほど、面白い。
僕の頭の中では数Aの範囲の最短経路問題が浮かんだ

こういうやつ、よく解きましたよね。
P地点を通って、AからBまで行くときの最短経路は何通りか、という問題。

AからPまでの行き方の総数と、PからBまでの行き方の総数を掛け算すれば求められる。
懐かしいですね〜

ここでABCの問題に戻ると
壊れた床同士の間にある床でそれぞれ何通り移動方法があるか求めて、
それらを掛け合わせれば良い。
簡単やん！と思ったが、

####移動方法は何通りだ？？
と我に返る。
いつだって僕の人生は行き当たりばったりで、一喜一憂を繰り返しているのだ。

そこで床の個数が1の場合、2の場合、、、と頭の中で計算をすると

| 続いている床の個数 | 移動方法の数 |
|:-----------------:|:------------------:|:------------------:|
| 1 | 1| This |
| 2 | 2 | column |
| 3 | 3 | will |
| 4 | 5 | be |
| 5 | 8 | center |
| : | :| aligned |

###フィボナッチ先生！！
フィボナッチ数列と言えば、

F0 = 0,
F1 = 1,
Fn + 2 = Fn + Fn + 1 (n ≧ 0)

皆さん大好きなこの漸化式。

自然界の至る所に見かけられますが、
有名なものだとひまわりの種の個数とか、オウムガイの螺旋構造とか、
黄金比にも行き着く、この素晴らしい数学の世界よ。

というわけで、もう頭の中では答えが完成。
あとはコードを書けばいいだけ。

ABC.py

#配列内の全ての数値の積を求める際に必要
from operator import mul
from functools import reduce
 
# リスト内包表記で入力を変数やリストに代入
n, m = [int(i) for i in input().split()]
arr = [int(input()) for i in range(m)]
 
#始点（0）と終点（n）をarrに追加するが、壊れた床間の差分をとる際にずれるので、視点は-1,終点は+1しておく
arr.append(n+1)
arr.insert(0, -1)
#壊れた床同士間にある床の数をリストに内包
div_arr = [arr[i+1]-arr[i]-1 for i in range(len(arr)-1)]

#フィボナッチ数列を定義
def Fib(n):
    a, b = 0, 1
    if n == 1:
        return a
    elif n == 2:
        return b
    else:
        for i in range(n-2):
            a, b = b, a + b
        return b
      
#div_arr内の全ての数をフィボナッチ数列の関数に入れ、それらを全て掛け合わせる
print(reduce(mul, [Fib(i+1) for i in div_arr])%1000000007)

以上、ABCのC問題の僕なりの解法でした。