Swin Transformerの実装を理解する

論文、コード、ライセンス

• Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, Baining Guo, Swin Transformer: Hierarchical Vision Transformer using Shifted Windows, arXiv:2103.14030, 2021
• コード(https://github.com/microsoft/Swin-Transformer)

掲載している画像は、引用元が本論文であり、本記事ではMITライセンスで公開されているコードを解説しています。ライセンス情報は以下の通りです。
Copyright (c) 2021 Microsoft Corporation.
The code snippets in this article are licensed under the MIT License.
See details at https://github.com/microsoft/Swin-Transformer/blob/main/LICENSE.

はじめに

論文では、Swin Transformerという新しいVision Transformerを提案しています。Vision Transformerは、自然言語処理で成功したTransformerを画像認識に適用した手法ですが、オリジナルのVision Transformerは、画像サイズが大きくなるほど計算複雑度が2乗に増大するという問題がありました。Swin Transformerは、この問題を解決するために、特徴マップを重なりのないウィンドウに分割し、各ウィンドウに対してself-attentionを計算するWindow-based Self-Attentionを採用しました。これにより、計算複雑度を線形に減らし、処理を高速化することができます。さらに、ウィンドウをずらしてアテンションを行うShifted Window-based Self-Attentionを組み込みむことで、隣接するウィンドウとの関連性を考慮した処理が可能になりました。また、Swin Transformerは、画像の細部から全体までの特徴を取得するために、パッチを結合して階層的に処理する構造を採用しています。これらの工夫により、画像分類、物体検出、セマンティックセグメンテーションの認識タスクにおいて、従来の手法よりも高い精度が得られています。
本記事では、Swin Transformerをどのようにコードで実装したかについて解説します。なお、Swin Transformerにはversion2も存在しますが、本記事ではversion1についてのみ取り上げます。

全体的なアーキテクチャ

Swin Transformerの全体的なアーキテクチャ(tiny version)を以下に示します。

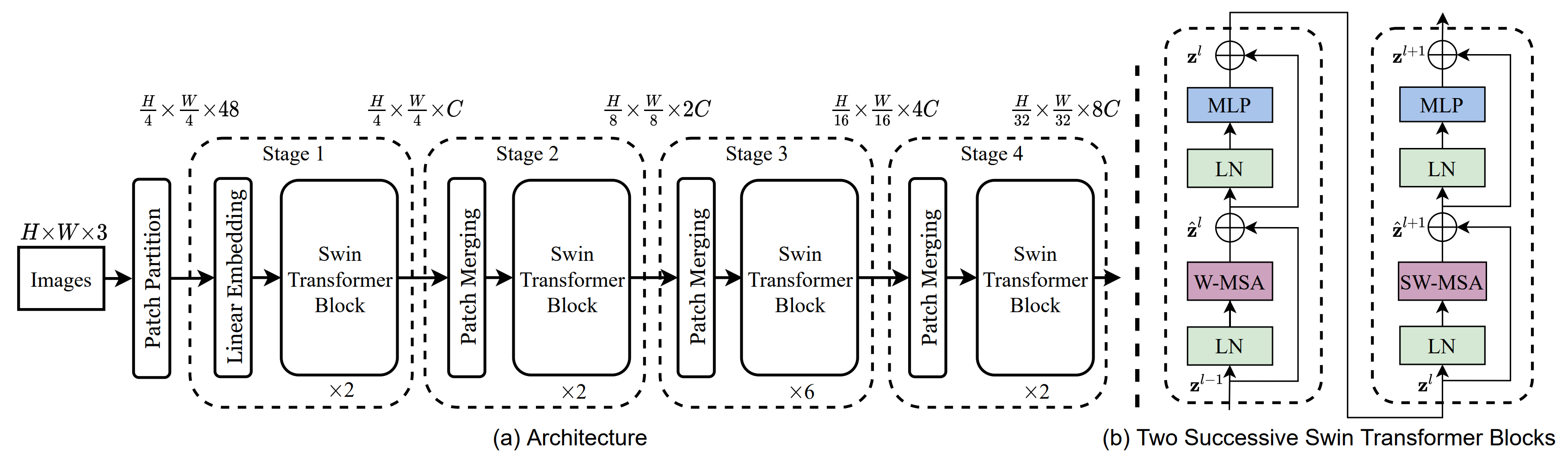
まず、Patch Partitionで、入力RGB画像を重ならないパッチに分割します。パッチサイズは$4\times 4$なので、各パッチのチャンネルの次元は$4\times 4\times 3=48$です。次に、Linear Embeddingを適用して、チャンネルの次元数を、任意の次元数Cに変換します。
Swin Transformer Blockでは、特徴マップをウィンドウに分割し、各ウィンドウで、Multi-head Self Attention(MSA)を適用します。MSAに適用するウィンドウの配置によって、Window-based MSA(W-MSA)とShifted W-MSA(SW-MSA)の2種類があります。(S)W-MSAの後は、分割されたウィンドウを元の特徴マップに戻し、残差結合、レイヤーノルム層(LN)、多層パーセプトロン(MLP)を適用します(上図(b))。Swin Transformer Blockは、入力と出力の次元を維持しながら、複数回実行されます。各実行で、W-MSAとSW-MSAを交互に呼び出します。上図(b)は2回実行したときの様子を示しています。
Patch Mergingは、複数のパッチを結合して、パッチ数を減らし、階層的な構造を作成します。結果として、解像度を半分、チャンネルを2倍にします。
Swin Transformerは、複数のSwin Transformer BlockとPatch Mergingを交互に繰り返し、画像の特徴を抽出します。

W-MSAとSW-MSA

Swin transformerでは、特徴マップをウィンドウ状に分割する方法として、2種類の方式を採用しています。

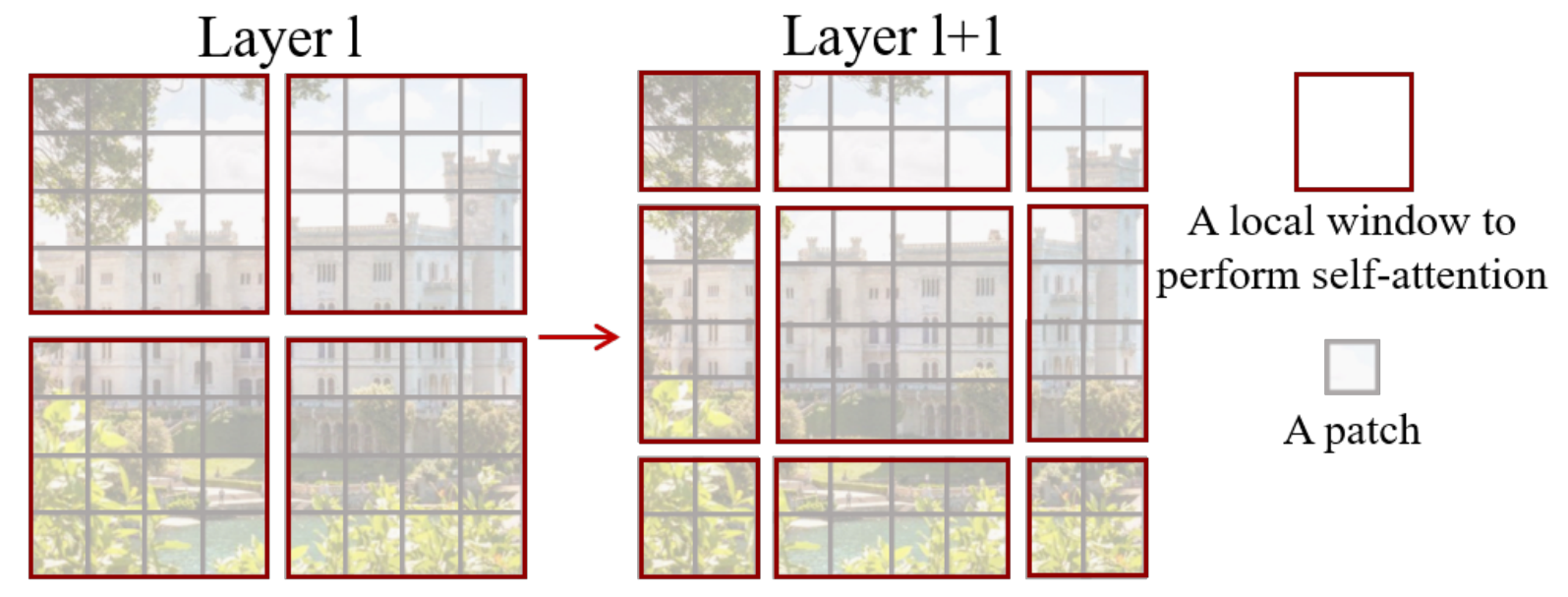
図の左側は、ウィンドウサイズ($M$)ごとに等間隔で分割する標準的な方法です。もうひとつは、ウィンドウサイズの半分$\lfloor M/2 \rfloor$だけシフトした位置から、ウィンドウサイズごとに分割するシフトした方法です。レイヤーごとに分割方式を交互に変えることで、ウィンドウ間での情報のやりとりが可能になります。ウィンドウを常に同じ方法で分割していると、そのウィンドウ内の情報しか得ることができませんが、ウィンドウをシフトすると、シフトしたウィンドウは、1つ前のレイヤーで分割された隣接のウィンドウと相互作用することができます。論文では、標準的な方法で分割してself-attentionを実行した方法をW-MSA、シフトを加えて分割した方法をSW-MSAと呼んでいます。
シフトさせた方法では、標準的な方法と比べて、ウィンドウ数が$\lceil h/M, w/M \rceil$から$\lceil h/M+1, w/M+1 \rceil$に増加します。ここで、$h$と$w$は特徴マップの縦と横のサイズを表します。また、一部のウィンドウは$M\times M$よりも小さくなります。小さなウィンドウと大きなウィンドウが混在すると、アルゴリズムの処理が複雑になります。単純な解決策としては、小さなウィンドウを$M\times M$をになるようにパディングしてやることです。そして、self-attentionを計算する際には、パディングされた部分はマスクして計算しないようにします。しかし、この方法では、ウィンドウ数が増加した分、計算時間も増加します。そのため、別の方法として、下図に示すように、上端と左側のウィンドウを下端と右側にもってくるように循環シフトを行います。

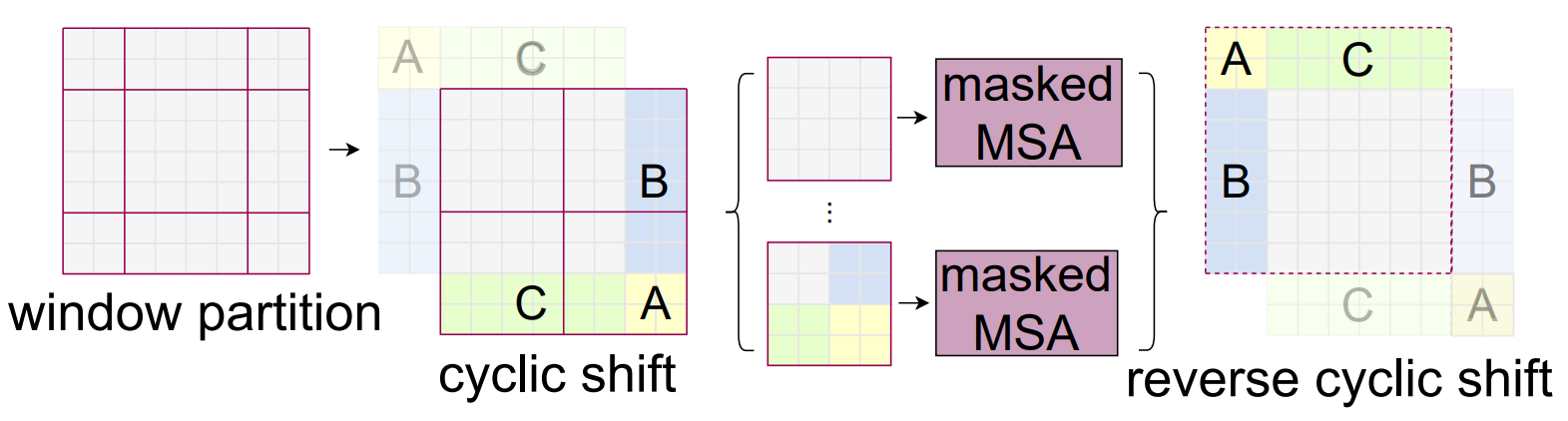
循環シフトを適用すると、シフトさせた位置は、元の位置と同じ位置に戻ります。そのため、標準的な分割方法でself-attentionを適用できます。しかし、上図(cyclic shift)に示すように、$M\times M$のウィンドウの中には、領域の異なるサブウィンドウが存在するため、self-attentionを実行するときはその部分を省いて計算する必要があります。例えば、右上の$M\times M$のウィンドウを見ると、縦長の異なる領域を持つサブウィンドウが2つ存在します。左側の縦長サブウィンドウは、右側の縦長サブウィンドウの情報を利用せずにself-attentionを実行する必要があります。そのため、計算領域を制限するためのマスクを導入します。マスクを導入することで、左側の縦長サブウィンドウは、左側の縦長サブウィンドウ内の情報のみを利用したself-attentionを実行できます。右側の縦長ウィンドウも同様です。また、左下と右下のウィンドウにも異なるサブウィンドウが存在しますが、ここでもマスクを利用して計算対象を制限します。self-attentionを実行した後は、サブウィンドウ領域を元の位置に戻すために逆循環シフトを行います(上図のreverse cyclic shift)。
W-MSAとSW-MSAは、以下で示すように、SwinTransformerBlockクラスで実装されています。SW-MSAは、torch.roll関数を使用して、(逆)循環シフトを行います。W-MSAとSW-MSAの違いは、このシフト処理とマスクの有無のみです。

class SwinTransformerBlock(nn.Module):
    ...
    def forward(self, x):
        ...
        # この時点で、xの形状は(B,H*W,C)=(バッチ数、特徴マップの高さ*横幅、チャンネル数)です
        # 残差結合用にxを保存します
        shortcut = x
        # nn.LayerNormを適用します
        x = self.norm1(x)
        x = x.view(B, H, W, C)

        # W-MSAまたはSW-MSAを実行します
        # C++/CUDAで書かれたウィンドウ分割/結合を行うメソッド呼び出しのコードは、省略します

        # SW-MSAの場合(self.shift_size>0)、循環シフトを適用します
        if self.shift_size > 0:
            shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
        else:
            shifted_x = x
        # HxWの特徴マップを、window_sizeの大きさのウィンドウに分割します
        # ウィンドウの数はnWで表され、バッチサイズと同じ軸に配置されます
        # 分割後のx_windowsの形状は、(nW*B, window_size, window_size, C)となります
        x_windows = window_partition(shifted_x, self.window_size)
        # ウィンドウベースのマルチヘッドアテンションを実行します
        # self.attnはWindowAttentionのforwardメソッドを呼び出します
        x_windows = x_windows.view(-1, self.window_size * self.window_size, C)
        attn_windows = self.attn(x_windows, mask=self.attn_mask)  # nW*B, window_size*window_size, C
        attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
        # nW個のウィンドウを結合して、HxWの特徴マップを作成します
        # 結合後のshifted_xの形状は、(B, H, W, C)となります
        shifted_x = window_reverse(attn_windows, self.window_size, H, W)
        # SW-MSAの場合、逆循環シフトを適用します
        if self.shift_size > 0:
            x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
        else:
            x = shifted_x

        x = x.view(B, H * W, C)
        # (S)W-MSAの後は、timm.models.layers.DropPathを使用して、ドロップアウトを適用します
        # その後、残差結合を行います
        x = shortcut + self.drop_path(x)
        # nn.LayerNormで正規化した後、多層パーセプトロンを適用します
        # その後、ドロップアウトを適用し、最後に残差結合します
        x = x + self.drop_path(self.mlp(self.norm2(x)))

        return x

# ウィンドウ分割
def window_partition(x, window_size):
    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
    return windows  # num_windows*B, window_size, window_size, C

# ウィンドウ結合
def window_reverse(windows, window_size, H, W):
    # windows: num_windows*B, window_size, window_size, C
    B = int(windows.shape[0] / (H * W / window_size / window_size))
    x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
    x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
    return x  # B, H, W, C

# ウィンドウベースのマルチヘッドアテンション
# Attention(Q, K, V) = softmax(Q * K^T / scale + bias) * V
# MultiHeadAttention(Q, K, V) = Concat(head_1, ..., head_n) * W_o
# ここで head_i = Attention(Q * W_i^Q, K * W_i^K, V * W_i^V) となります
class WindowAttention(nn.Module):
    ...
    def forward(self, x, mask=None):
        B_, N, C = x.shape
        # self.qkvは、入力次元Cから出力次元3Cに変換する全結合層です
        qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)  # 3, B_, nH, N, C'
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        # スケール変換を行い、アテンションスコアを獲得します
        q = q * self.scale
        attn = (q @ k.transpose(-2, -1))  # B_, nH, N, N

        # 相対位置バイアスを追加します (後述する)
        relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
            self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
        relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
        attn = attn + relative_position_bias.unsqueeze(0)

        # SW-MSAでは、softmaxを適用する前に、マスクを追加します
        # 一方、W-MSAでは、マスクを利用せず、そのままsoftmaxを適用します
        if mask is not None:
            nW = mask.shape[0]  # nWはウィンドウの数を表す
            attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
            attn = attn.view(-1, self.num_heads, N, N)
            attn = self.softmax(attn)
        else:
            attn = self.softmax(attn)
        # ドロップアウト層を適用します
        attn = self.attn_drop(attn)  # B_, nH, N, N

        # アテンションを計算します
        x = (attn @ v).transpose(1, 2).reshape(B_, N, C)  # B_, nH, N, C' -> B_, nH, C', N -> B_, N, C
        # 入力次元Cのベクトルを、同じく入力次元Cのベクトルに変換する全結合層を適用します
        x = self.proj(x)
        # ドロップアウト層を適用します
        x = self.proj_drop(x)
        return x

アテンション用のマスクは、以下の方法で作成されます。

# 循環シフトを適用してウィンドウ分割した領域は、ウィンドウ領域とサブウィンドウ領域に分けられます。
# 以下のimg_maskには、各領域を識別するための領域番号が割り当てられています
# 例えば、H, W, window_size, shift_size = 4, 4, 2, 1の場合、img_mask[0, :, :, 0]は次のようになります
#     tensor([[0., 0., 1., 2.],
#             [0., 0., 1., 2.],
#             [3., 3., 4., 5.],
#             [6., 6., 7., 8.]])
# アテンションはウィンドウ単位で行われるため、例えば、右上のウィンドウ(1と2)では、
# サブウィンドウ領域1は、サブウィンドウ領域2の情報を使用せずにアテンションを計算する必要があります
# 以降では、この右上のウィンドウ領域に注目して解説します
H, W = self.input_resolution
img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
h_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
w_slices = (slice(0, -self.window_size),
            slice(-self.window_size, -self.shift_size),
            slice(-self.shift_size, None))
cnt = 0
for h in h_slices:
    for w in w_slices:
        img_mask[:, h, w, :] = cnt
        cnt += 1

# img_maskをウィンドウごとに分割し、ウィンドウ数、縦のウィンドウサイズ、
# 横のウィンドウサイズ、チャンネル数(=1)の順に並んだ4次元配列mask_windowsを作成します
# 先程の例の場合、mask_windows[1]は右上のウィンドウを表します
# 具体的には、次のように領域番号が格納されます
#     mask_windows[1, :, :, 0] = tensor([[1., 2.],
#                                        [1., 2.]])
mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1
# 縦横のウィンドウの次元を1つに統合します
# チャンネル数は1なので、その次元は削除できます
# 結果として、mask_windows[1] = tensor([1., 2., 1., 2.])となります
mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
# 上記の分割処理(window_partition)と次元変換(view)は、(S)W-MSAのコードでも同様の処理が行われています
# 具体的には、以下の部分です
#     x_windows = window_partition(shifted_x, self.window_size)
#     x_windows = x_windows.view(-1, self.window_size * self.window_size, C)
# このため、x_windowsに対応する領域番号は、mask_windowsが格納しています
# この後、アテンションが実行されます
# まず、全結合層と次元変換を行います
#     qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
#     q, k, v = qkv[0], qkv[1], qkv[2]
# この処理はチャンネル方向に適用されるため、空間方向に関係するmask_windowsとは無関係です
# したがって、mask_windowsの変換は必要ありません
# 次は、qとkの転置による内積計算です
#     attn = (q @ k.transpose(-2, -1))
# qとkの形状は(B_, nH, N, C')=(バッチ数*ウィンドウ数, ヘッド数, ウィンドウサイズ*ウィンドウサイズ, チャンネル数)です
# N方向が空間位置を表すので、内積計算によってmask_windowsも変換する必要があります
# 先程の例で考えると、つまり、バッチ数=1、N=4、mask_windows[1]=tensor([1., 2., 1., 2.])の場合、
# 1番目のウィンドウのq[1,0]=[q1,q2,q3,q4]とk[1,0]=[k1,k2,k3,k4]の内積は次のようになります
#         k1       k2       k3       k4
#        [<q1,k1>  <q1,k2>  <q1,k3>  <q1,k4>]  q1
# attn = [<q2,k1>  <q2,k2>  <q2,k3>  <q2,k4>]  q2
#        [<q3,k1>  <q3,k2>  <q3,k3>  <q3,k4>]  q3
#        [<q4,k1>  <q4,k2>  <q4,k3>  <q4,k4>]  q4
# これと同様な操作を、mask_windowsにも適用します
# つまり、mask_windows[1]の1,2,1,2を縦と横に並べて、クロスさせたときに、各要素がどの領域に当たるかを考えます
# 例えば、左上の要素(attn[0,0])は、領域1と領域1の内積計算になるため、領域1の情報を表します(下図左側参照)
# しかし、その右隣の要素(attn[0,1])は、領域1の情報と領域2の情報を用いて内積計算をしています
# アテンションの計算では、異なる領域の情報を使用してはいけないため、attn[0,1]は計算対象から除外する必要があります
# このように、attnにはマスクする位置とマスクしない位置があります
# マスクしない位置を「o」で、マスクする位置を「x」で表すと、下図右側のようになります
#     1  2  1  2             1 2 1 2
#     |     |  |           1 o x o x
# 1 --1     |  |    --->   2 x o x o
# 2 --------x  |           1 o x o x
# 1            |           2 x o x o
# 2 -----------2
# このマスク判別をコードで表すと、以下のようになります
# attn_maskの要素が0ならマスクしないことを、それ以外の値ならマスクすることを表します
# (mask_windowsは領域番号を表していましたが、attn_maskはマスクの有無を表します)
attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
# マスクは、softmax(attn + attn_mask)の計算で使用されます
# この値をnew_attnとします
# マスクされた位置のnew_attnの値は、理想的には0にすることです
# これは、new_attnとvの内積を計算する際に、マスクに対応するvの要素を内積計算から除外できるからです
# マスクされた位置のnew_attnの値を0にするには、マスクされた位置のattn_maskを大きな負の値にすることです
# これは、softmax関数において、大きな負の値をexp関数に入力すると、その出力がほぼ0になるからです
# 以下のコードでは、マスクされた位置のattn_maskの値を-100、マスクしない位置のattn_maskを0に設定しています
attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

MSAとW-MSAの計算複雑度

特徴マップのサイズが$h\times w$で、各ウィンドウ内に$M\times M$個のパッチが含まれている場合、MSAとW-MSAの計算複雑度は次のように表されます。

\displaylines{
\Omega(MSA) = 4hwC^2 + 2(hw)^2 C \\
\Omega(W\hspace{-0.2cm}-\hspace{-0.2cm}MSA) = 4hwC^2 + 2M^2hwC
}

MSAの計算複雑度はパッチ数$hw$の2乗に比例します。一方、W-MSAでは$M$(デフォルト7)を固定したときパッチ数に比例します。このため、W-MSAはスケーラビリティが高いといえます。
なお、MSAとW-MSAの計算複雑度は以下の計算式から導かれたものと考えられます。

# 以下のコードで示すように、各ウィンドウのMSAの計算複雑度は、次のように表されます
# 計算複雑度 = qkvの全結合層による線形変換 + qとkの内積計算 + アテンションスコアとvの内積計算 + 最後の全結合層による線形変換
#            = 3*N*C^2 + C*N^2 + C*N^2 + N*C^2
#            = 4*N*C^2 + 2*C*N^2
# ここで、Nはウィンドウ内のパッチ数、Cはチャンネル数です
# W-MSAの場合、Nはウィンドウサイズ(M)の2乗であるため、全ウィンドウ(h/M * w/M)でのMSAの計算複雑度は、次のようになります
# 計算複雑度 = h/M * w/M * (4*M^2*C^2 + 2*C*M^4)
#            = 4*h*w*C^2 + 2*h*w*C*M^2
# また、通常のMSAの場合、Nはh*wであるため、計算複雑度は 4*h*w*C^2 + 2*C*(h*w)^2 となります

class WindowAttention(nn.Module):
    ...
    def forward(self, x, mask=None):
        # B_を1としたときの計算量を求めます
        # Cはself.num_headsで割り切れるとします
        B_, N, C = x.shape
        ...

        # xの形状が(B_,N,C)で、self.qkvがnn.Linear(C, 3C)で作成されているため、
        # self.qkv(x)の計算量は N * C * 3C となります
        qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        ...
        # qとkの形状が(B_,self.num_heads,N,C/self.num_heads)であるため、
        # qとk転置の内積計算量は self.num_heads * C/self.num_heads * N * N となります
        attn = (q @ k.transpose(-2, -1))
        ...
        # attnとvの形状がそれぞれ(B_,self.num_heads,N,N)と(B_,self.num_heads,N,C/self.num_heads)であるため、
        # attnとvの内積計算量は self.num_heads * N * N * C/self.num_heads となります
        x = (attn @ v).transpose(1, 2).reshape(B_, N, C)

        # xの形状が(B_,N,C)で、self.projがnn.Linear(C, C)で作成されているため、
        # self.proj(x)の計算量は N * C * C となります
        x = self.proj(x)
        ...

Relative Position Bias

アテンションの大きさは、$Q$と$K$の類似度によって大きく影響を受けますが、$Q$と$K$の位置関係もアテンションの大きさに影響を与える可能性があります。例えば、$Q$と$K$が近い位置にある場合、それらの間には強い関連性があるため、アテンションの大きさも大きくなると考えられます。そこで、$Q$と$K$の位置関係を考慮したバイアスを導入することが提案されています。

\displaylines{
\mathrm{Attention}(Q,K,V) = \mathrm{SoftMax}(QK^T/\sqrt{d}+B)V
}

ここで、$Q,K,V \in \mathbb{R}^{M^2\times d}$はquery、key、valueの行列です。$d$はquery/keyの次元数です。$M^2$はウィンドウ内のパッチ数です。$B \in \mathbb{R}^{M^2\times M^2}$はバイアスです。
ウィンドウのサイズは$M$なので、$Q$と$K$の位置はそれぞれ$M^2$通り存在します。そのため、単純な方法では、$Q$と$K$の各組み合わせに対応する$M^2\times M^2$次元のバイアスを訓練します。しかし、この方法では、パラメータの数が膨大になるという問題があります。そこで、より本質的な方法として、$Q$と$K$の相対的な位置関係を考慮したRelative Position Biasを導入します。Relative Position Biasは、$Q$と$K$の横方向の相対位置($-M+1$から$M-1$までの$2M+1$通り)と縦方向の相対位置($-M+1$から$M-1$までの$2M+1$通り)の組み合わせで表されます。例えば、$Q$と$K$がウィンドウの左端と右端にある場合、横方向の相対位置は$M-1$となります。逆に、$Q$と$K$がウィンドウの右端と左端にある場合、相対位置は$-M+1$となります。そのため、Relative Position Biasの次元は${(2M+1)\times (2M+1)}$となります。$M$が大きくなるほど、単純な方法よりもパラメータ量を節約できます。そこで、$(2M-1)\times (2M-1)$の小さなバイアス行列$\hat{B}$を訓練させ、$B$の値は$\hat{B}$から与えることにします。
実装では、$B$の各要素が$\hat{B}$のどの要素を使用するかを、相対位置インデックスで指定します。そのため、$B$と同じ大きさの行列を用意し、各要素に相対位置インデックスを格納します。このインデックスを使用して、バイアス値を格納しているテーブルからバイアス値を取得します。以下は、相対位置インデックスを求めるコードの解説です。

# ウィンドウサイズが(2,2)の場合を考えます
# つまり、self.window_size=(2,2)=(Wh,Ww)です
# このとき、最後に計算される相対位置インデックスを示す行列(relative_position_index)は以下のようになります
# tensor([[4, 3, 1, 0],
#         [5, 4, 2, 1],
#         [7, 6, 4, 3],
#         [8, 7, 5, 4]])
# 行列の大きさは(Wh*Ww,Wh*Ww)です
# 右上が最小値の0で、左下に向かうほど、値は右下方向から見ると大きくなります
# 対角方向には最大値と最小値の中間値である4が、左下には最大値の8=(2*Wh-1)*(2*Ww-1)-1が格納します
# 原点が右上となる相対位置の値が得られています
# このような特徴は、ウィンドウサイズを変えても変わりません
#
# この相対位置インデックスは、次の部分で使用されています
#     attn = q @ k^T + rpb_table[rp_index.view(-1)].view(...).permute(...).contiguous().unsqueeze(0)
# q@k^Tはqとk転置の内積計算、rpb_tableは相対位置バイアスを格納したテーブル、rp_indexは相対位置インデックスを表します
# rpb_tableの形状は((2*Wh-1)*(2*Ww-1)-1,num_heads)です
# したがって、インデックスは0から(2*Wh-1)*(2*Ww-1)-1までの整数値を使用します
# また、この範囲のすべての整数値を使用する必要があります
# 以下のコードでは、rp_indexがこの条件を満たすことと、右上を原点とする相対位置が得られることを解説します

# 指定した範囲の整数値の配列を生成する
coords_h = torch.arange(self.window_size[0])  # 形状は Wh
coords_w = torch.arange(self.window_size[1])  # 形状は Ww
# tensor([0, 1])
# tensor([0, 1])

# torch.meshgridによって縦方向と横方向の座標を示すテンソルが得られます
# torch.tensorで1つのテンソルに結合します
# coords[0]は上から順に値が大きくなり、coords[1]は左から順に値が大きくなります
coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
# tensor([[[0, 0],
#          [1, 1]],
#
#         [[0, 1],
#          [0, 1]]])

# coordsの1番目の軸を平坦化します
coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
# tensor([[0, 0, 1, 1],
#         [0, 1, 0, 1]])

# relative_coords[0]とrelative_coords[1]の行列を、ウィンドウサイズ(=2x2)ごとに分割すると、
# relative_coords[0]の場合、各ウィンドウ内の値はすべて同じ値になり、ウィンドウ全体としては左下に向かうほど値が大きくなります
# relative_coords[1]の場合、各ウィンドウ内の値は左下に向かうほど大きくなります
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
# tensor([[[ 0,  0, -1, -1],
#          [ 0,  0, -1, -1],
#          [ 1,  1,  0,  0],
#          [ 1,  1,  0,  0]],
#
#         [[ 0, -1,  0, -1],
#          [ 1,  0,  1,  0],
#          [ 0, -1,  0, -1],
#          [ 1,  0,  1,  0]]])

# 以下のコードは次のコードと同じです
#     relative_coords[0] += window_size[0] - 1
#     relative_coords[1] += window_size[1] - 1
#     relative_coords[0] *= 2 * window_size[1] - 1
#     relative_position_index = relative_coords.sum(0)
# relative_coords[0]は足し算と掛け算を、relative_coords[1]は足し算をします
# 最後に、relative_coords[0]とrelative_coords[1]を合算します
# 結果は次の通りです
# tensor([[[1, 1, 0, 0],          tensor([[[3, 3, 0, 0],
#          [1, 1, 0, 0],    mul            [3, 3, 0, 0],
#          [2, 2, 1, 1],    --->           [6, 6, 3, 3],         tensor([[4, 3, 1, 0],
#          [2, 2, 1, 1]],                  [6, 6, 3, 3]]   sum           [5, 4, 2, 1],
#                                                          --->          [7, 6, 4, 3],
#         [[1, 0, 1, 0],                  [[1, 0, 1, 0],                 [8, 7, 5, 4]])
#          [2, 1, 2, 1],                   [2, 1, 2, 1],
#          [1, 0, 1, 0],                   [1, 0, 1, 0],
#          [2, 1, 2, 1]]])                 [2, 1, 2, 1]]])
# 足し算後、relative_coords[0]は0から2*Wh-2までの、relative_coords[1]は0から2*Ww-2までの整数値を持ちます
# 掛け算後、relative_coords[0]の値は0,2*Ww-1,...,(2*Wh-2)*(2*Ww-1)の範囲になります
# したがって、合算後は、右上隅のウィンドウ付近を見ると、次のようになります
# [ ... 2*Ww-1 | Ww-1   Ww-2   ... 0      ]
# [ ... 2*Ww   | Ww     Ww-1   ... 1      ]
# [ ...        |               ...        ]
# [ ... 3*Ww-2 | 2*Ww-2 2*Ww-3 ... Ww-1   ]
# [------------+--------------------------]
# [ ... 4*Ww-2 | 3*Ww-2 3*Ww-3 ... 2*Ww-1 ]
# [ ...        |               ...        ]
# ここで、縦線(|)と横線(-)はウィンドウの境界を表します
# 右上のウィンドウには、0から2*Ww-2までの整数値が連続して格納されます
# その隣のウィドウには、その続きの2*Ww-1から4*Ww-1までの整数値が連続して格納されます
# これを繰り返すと、ウィンドウ全体には、0から(2*Wh-1)*(2*Ww-1)-1までの整数値が連続して格納されます
# したがって、relative_position_indexは、指定範囲の整数値をすべて使用します
# また、ウィンドウ内部の値は、左側または下側に進むと、1ずつ増加します
# ウィンドウの境界を超えると、値はWwに応じてさらに大きくなります
# そのため、ウィンドウ全体に対しても、左下に向かうほど右下方向から見て値が大きくなります
# したがって、relative_position_indexは、右上を原点とする相対位置を表します
relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww

MLP

MLPは、入力層と出力層の間に2層の全結合層を配置し、その間に非線形活性化関数のGELUを適用します。以下は実装です。

class Mlp(nn.Module):
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        ...
        # 入力層と出力層のユニット数は等しいです(in_features=out_features)
        # デフォルトでは、中間層のユニット数は入力層のユニット数の4倍です(hidden_features=4*in_features)
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x

Patch Embedding

Patch Embeddingは、入力画像を重なりのないパッチに分割するPatch Partitionと、チャンネル数を任意の次元(C)に埋め込むLinear Embeddingを組み合わせたものです。これをnn.Conv2dを用いて実装します。nn.Conv2dのカーネルサイズとストライド幅をパッチサイズに設定することで、重なりのないパッチに分割することができます。また、出力チャンネル数をCに設定することで、チャンネル数も変換できます。以下は実装です。

class PatchEmbed(nn.Module):

    def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
        ...
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
        ...

    def forward(self, x):
        ...
        # xの形状は(B,in_chans,H,W)から(B,H/p*W/p,C)に変換されます
        # HとWは入力画像の縦と横のサイズ、pはパッチサイズ、Cはチャンネル数です
        x = self.proj(x).flatten(2).transpose(1, 2)
        # デフォルトではnn.LayerNormを適用します
        if self.norm is not None:
            x = self.norm(x)
        return x

Patch Merging

Patch Mergingは、$2\times 2$の隣接するパッチを連結することで、パッチ数を1/4に減らし、チャンネル数を4倍にします。その後、全結合層によってチャンネル数を半分に減らします。以下は実装です。

class PatchMerging(nn.Module):

    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        ...
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        ...
        # パッチを連結します
        # この時点でのxの形状は(B,H,W,C)です
        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C

        # nn.LayerNormを適用します
        x = self.norm(x)
        # 全結合層により、チャンネルの次元を4Cから2Cに変換します
        x = self.reduction(x)

        return x

BasicLayerとSwinTransformer

BasicLayerは、SwinTransformerBlockを複数回実行した後、PatchMergingを実行します。ただし、最後のレイヤーではPatchMergingは行われません。
SwinTransformerのエントリーポイントでは、まず入力画像をPatchEmbedでパッチ化します。その後、BasicLayerをデフォルトでは4回繰り返して、画像の特徴を抽出します。最後に、クラス分類を行います。

class BasicLayer(nn.Module):

    def __init__(...):
        ...
        self.blocks = nn.ModuleList([
            SwinTransformerBlock(...
                                 # SwinTransformerBlockを呼び出すごとに分割方式を交互に変えます
                                 # shift_size=0の場合は標準的な分割方法、それ以外の場合はシフトした分割方法を採用します
                                 shift_size=0 if (i % 2 == 0) else window_size // 2,
                                 ...)
            for i in range(depth)])
        ...

    def forward(self, x):
        # SwinTransformerBlockを適用します
        for blk in self.blocks:
            if self.use_checkpoint:
                # torch.utils.checkpointモジュールのcheckpoint関数を実行します
                # メモリを節約するために、計算グラフを保存せず、逆伝播時に再計算します
                x = checkpoint.checkpoint(blk, x)
            else:
                x = blk(x)
        # PatchMergingを適用します
        if self.downsample is not None:
            x = self.downsample(x)
        return x


class SwinTransformer(nn.Module):
    ...
    def forward_features(self, x):
        # PatchEmbedを適用します
        x = self.patch_embed(x)
        # デフォルトでは絶対位置埋め込みを使用しません
        # これは、論文によると、絶対位置埋め込みと相対位置バイアスを同時に使用すると、
        # 精度が低下するという実験結果に基づいていると思われます
        if self.ape:
            x = x + self.absolute_pos_embed
        # Dropoutを適用します
        x = self.pos_drop(x)

        # BasicLayerを適用します(デフォルトは4回実行します)
        for layer in self.layers:
            x = layer(x)

        # nn.LayerNormを適用します
        x = self.norm(x)  # B L C
        # nn.AdaptiveAvgPool1d(1)を適用して空間次元を1にします
        x = self.avgpool(x.transpose(1, 2))  # B C 1
        x = torch.flatten(x, 1)  # B C
        return x

    def forward(self, x):
        x = self.forward_features(x)
        # 全結合層を適用して、(B,C)から(B,クラス数)に変換します
        x = self.head(x)
        return x

おわりに

Swin Transformerは、局所的なウィンドウ内でself-attentionを用いることで、計算量を線形に抑えながら、階層的な構造を採用した新しいVision Transformerです。本記事では、Swin Transformerの手法と実装について解説しました。特に、マスクの生成方法と相対位置インデックスを求めるコードは、理解に時間を要したため、コメントを多めに残しました。この記事が誰かの助けになれば幸いです。