初めまして。落語でいうところの「トリ」を務めさせて頂くポンコツLisperです。
この投稿の狙い
繰り返しは人の技、再帰は神の技。というツイートを最近ツイッターで見かけました。
成程、なかなかいい得て妙、という気がします。Lisperならおおむね同感なのではないでしょうか?
ですがその神業の再帰に頼り切ってコードを書いて、それでうまくいったからあとは野となれ山と
なれ、というのはどうでしょう?
再帰を現実のものとするLisp処理系の内側で、何が起こっているのかについて展望を持っておくのも、
Lisperとしてのスキルアップに必要なことの一つだと思います。
今を去ること三十余年、私は人工知能の研究を目指してLisp処理系を探し始めました。貧乏学生の
分際でも手に入る処理系です。ですが現実は厳しかったです。Lispマシンは当時としては理想
でしたが、高価すぎて到底手の出るものではありません。それどころか16ビットPCさえ買うお金が
ないのです。苦し紛れに8ビットPCを手に入れてみましたが、これで動かせるLisp処理系は子供騙し
でさえありません。やむを得ず自分の手で処理系を作ることとしました。
これは、その過程で私が出会った「逆転ポインタ法」なるテクニックを紹介し、再帰とは何かを
考察するレポートです。
MPLispとその背景
私が作った処理系は、最初のウォーミングアップとして大学のメインフレームでHLisp(日立Lisp)
上に書いたMPLisp ver1.1と、Z80アセンブラを意識してBasic上に書いたver2.2で、Most Primtive Lisp
の意味です。その開発は成功裏に終了し、文字通りPrimitiveながらも循環リストに耐えるprintと
同じくガーベジコレクタ(以下単にGC)、そしてマクロ機能のカーネル部を組み込んだインタプリタが
実現しました。生意気にもフォールトトレラントを自認する出来栄えとなっています。
然し開発は一本道ではありませんでした。何しろ兎に角メインメモリが64KBしかありません。
しかもそのうち36KBをBasicインタプリタが分捕ってしまうのです。
スピードも、3.58MHzの8bitPCで二重インタプリタ(BasicインタプリタがMPLispインタプリタの
コードを実行する)ともなると気が遠くなるほど遅くなります。
今のPCでは、スピードもGHz単位ですし、メモリもGB単位となっています。TB単位のHDDまでもが
完備されています。そんなヂヂイの大昔の話をされても何の参考にもならないと仰る方も多いかも
しれません。ですがこれだけ恵まれた環境でも、尚もメモリ不足や実行速度の遅さに手を焼いている
プログラマは少なくない筈です。そこでこのような昔話を蒸し返して今のLisper諸兄に何らかの
ヒントになるものがあるのではないかと思い立ったわけです。
GCの実際
ご存知の通り、Lisp処理系はconsで利用したセルをそのまま野ざらしにしてしまいますのでいずれ
尽きてしまいます。そこで現存するセルのうち利用中のものと役目を終えてしまったものをより
分けて、役目を終えたものをかき集めてフリーリストに戻す仕組みが必要になります。これを行う
のがご存知の通りガーベジコレクタです。
GCは、使用中のセルを検出して回収の対象から外すmarkingのステップと、検出されなかったセルを
かき集めるcollectionのステップによって成り立っています。この内collectionのステップは単純な
繰り返しによって実行されるものが多いので、セルを実現するデータ構造さえ設計すればほぼ自動的
に決まる場合が多いです。(そうでない構造の処理系もあります。例えば線形化圧縮ガーベジ
コレクタを採用している処理系などです。)そこでmarkingをいかに行うかが一つの焦点となって
きます。
GCの現実
使用中のセルが多くなると、その数に比例してmarkingに時間がかかります。と同時に回収される
セルの数が減ります。回収されるセルが少なくなるとGCの行われる頻度が高くなります。こうして
実行時間に占めるGCの比重が大きくなっていきます。悪いことに、markingを再帰によって書いて
あると、GCがたくさんのスタック(それも使用中のセルの数にほぼ比例した数だけ)を消費する
ので、スタックオーバーフローを起こしやすくなります。もっと悪いことに、複雑なプロぎラムを
実行する時にはスタックの消費量も使用中のセルの数も増えてしまいます。こうしてLispプログラム
は複雑になればなるほどメモリの使用量が増えて、実行時間も加速度的に(というかもっと深刻に)
増大していきます。
もしGCの最中にスタックオーバーフローを起こすと致命的なエラーとなり、実行の継続は不可能と
なります。MPLispの時代に有名だったUTILispはこれによって処理系自体がアボートする設計に
なっていました。これを回避するためにより多くのメモリを使うように変更すると、実行速度が犠牲
になります。このような矛盾を回避しようと考案されたのが逆転ポインタ法です。
残念なことに、私が最初に逆転ポインタ法に出会った本は、度重なる引っ越しによって、どこに
しまったか判らなくなってしまい、著者のお名前も本のタイトルも思い出せなくなってしまい
ました。更に、MPLispのソースリストさえ行方不明になってしまって、当時実装したコードを思い
出させるものは拙い記憶だけとなってしまいました。この記事のもう少し後のほうに逆転ポインタ法
のコードを掲載しますが、これはその拙い記憶を辿って再現したものです。
逆転ポインタ法とは
二進木構造を現実のものにするセル領域に於いて、リストは再帰的な表現によって実現されて
います。その構造を辿ってmarkingしていくコードを実装するには、再帰を使ってコーディングす
るのが自然な方法です。ですが、再帰を使ってコードを書くと、制御の流れを決定するために
戻り先をスタックに積む必要があります。また作業用変数の値を、呼び出す側から戻った時に呼び
出した側のものに復元してやるためにも、この値をスタックに積む必要があります。
ここで、今markingしている最中の二進木構造の中に、作業用変数の値をスタックに代わって、
格納しておくスキマがあるのです。実は、今markingしているセルの(car、cdrの各)ポインタ
を、指しているほうから、指されている根元を向かせるように使えば、
セルのアドレス(正確にはポインタ)をスタックに積む必要がなくなるのです。
ここで、私は大変なバカ頭なので、書いていて何が何だか解らなくなって来ました。そこで図解を
ご覧ください。(ここで、私は最近手が不自由になってしまって鉛筆が持てないもんですから
ひどい図になってしまいました。我慢してください。)
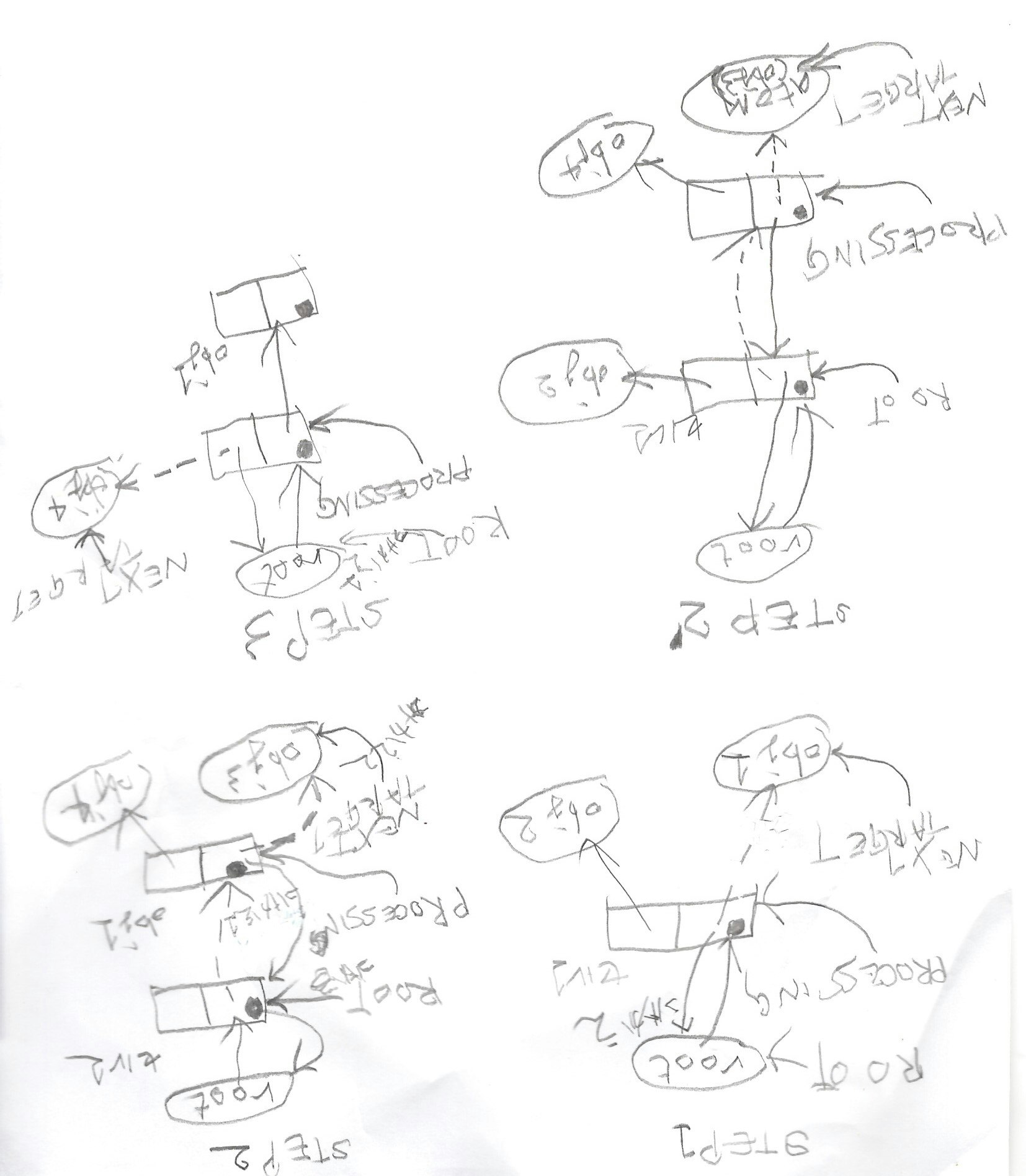
図1に於いて、ROOT、PROCESSING、NEXTTARGETというのは(多分汎用レジスタに
割り当てられる)作業用変数で、ポインタです。この三つは、Z80の汎用レジスタ(?)である
HL、DE、BCの各レジスタに割り当てられるつもりでした。
さて図1のステップ1に於いて、rootと書かれたオブジェクト(セルとは限りません)は今marking
の対象となったセル (Bセル1)を指すポインタで、ROOTがrootを指しています。ドミノの
ようなものはセル(セル1)に於いて、左半分はcar部分で右半分はcdr部分です。このセル(セル1)を今PROCESSINGが指しています。ここで今このセル(セル1)をマーク(黒丸)して、次にこのセルのcar部分が指すobject(obj1)(それは往々にしてセルです。セルの場合これを新たな起点にしてmarkingを行う必要があります。手順は深さ優先探索となります)をマークします。この時、ROOTにPROCESSINGの値を(ROOTがセル1を向く)、PROCESSINGの指すセル(セル1)のcar部分にROOTの値を(ステップ1-1の「つけかえ」)、PROCESSINGにNEXTTARGET、9PPの値(obj3のアドレス)を、そして(もし次のターゲット(obj1)がセルなら)NEXTTARGETの指すセル(obj3)car部分の値(obj3のアドレス)をNEXTTARGETに代入することになります(ステップ2)。(セルでなければ、PROCESSINGの指すオブジェクト(obj1)を単にmarkします:ステップ2’)そしてPROCESSINGとROOTの値を元に戻して(PROCESSINGにROOTの値を(PROCESSINGがobj1を向く)、NEXTTARGETにPROCESSINGの指すcar部分の値(obj3のアドレス)をcdr部分の指すobject(OBJ2)を同様にマークする
(ステップ3)、という流れになります。NEXTTARGETの指すセル(その時にはPROCESSINGが
指しています)をmarkする、つまり再帰のネスティングレベルの一つ増えた処理、を行うときに
ROOTとPROCESSINGの値をスタックに積んでおかなくては処理を終えて引き返してくるときに
戻りようがなくなってしまいます。この時スタックを使う代わりにROOTの値をPROCESSINGの指す
car部分(或いはcdr部分)に代入しておくのです。このステップで、ポインタが逆向きの矢印に
なってしまうために逆転ポインタ法の名前がつけられたのです。戻るときには、ROOTの値から
PROCESSINGの値を復元し、その後PROCESSINGの指すcar(或いはcdr)からROOTの値を復元する
ことになります。これによってソROOTとPROCESSINGをスタックに積む必要がなくなります。
そして、肝心なことですが、NEXTTARGETの値から(復元された)PROCESSINGの指すcar(或いは
cdr)部分を復元します。NEXTTARGETを復元する必要はありません。
以上が逆転ポインタ法の本質的な部分です。元の本ではもっとずっと簡潔な日本語で書かれていた
ため、文章としては勿論遥かに優れていましたが、当時の私には大変難解でした。しかもコードは
何一つ載っていなかったため、コーディングに於いては大変な困難を伴いました。やはりバカ頭
なんですね。オマケにLisperとしては全くのポンコツです。
さて、これだけでは完全なスタック無しにはなりません。再帰的に呼び出すときに、戻り先を
スタックに積むようにしてしまっては頭隠して何とやらです。つまり、恐ろしいことにgosub文を
使ってはいけないのです。故にgoto文でrecursionを実装しなければならないのです。return文も
goto文にする必要があります。ですが、ここでちょっと寄り道をしなければなりません。入門し
たてのLisperにはもうちょっと初歩的な解説が必要であることに気づいたのです。
GCの基礎
ここでは、Lisp処理系における基礎的なデータ構造とGCにおけるデータ操作の基本について書き
ます。独自の処理系をご自分でこれから実装したいという方だけ軽く目を通しておいてください。
フリーリスト
Lisp処理系がスタートアップするとき、主記憶の構造を作る処理が必要になります。その一つに
フリーリストがあります。スタートアップ時、セル領域にはまだ使われていないセルがぎっしり
並んでいます。そのcar部分は何であってもいいのですが、cdr部分は次の未使用セルを指して
いる必要があります。末尾のセルのcdr部はnilを指している必要があります。そして、主記憶上の
固定されたアドレスに、freeというポインタを置いておいて、先頭の未使用セルを指させておき
ます。この、freeから辿って行って末尾のnilを見つけるまで辿ることのできるリストをフリーリスト
といいます。これがないとconsは新しいセルを供給できません。セルを消費するたび、freeの指して
いるセルを消費して、freeの値をfreeの指すcdrの値を以て置き換えていきます。freeがnilを指して
いたら直ちにGCを起動します。GCとは、このフリーリストを作り直す操作にほかなりません。
シンボル領域
ここで「領域」という言葉を使うと誤解を生むかもしれません。メモリを予め区切っておくような
データ構造でなくても処理系は実装できるからです。因みにMPLispは細かく区切っていました。
シンボルにはいくつかの属性がつきものです。どのシンボルにも必ずひとつ与えられている属性と
して、印字名があります。ほかに、関数としての定義、変数としての値、PLISTなどが挙げられ
ますが、印字名以外は必ずしも全てのシンボルに与えられているとは限りません。そのような属性を
表すデータ構造をどのように実現、実装するかは、どんな属性を持たせるかと並んで、処理系制作者
の腕の見せ所といえるでしょう。シンボルごとに決まったエリアを設けるとか、ポインタだけ置い
ておいて実体はほかに置いておくとか、別にテーブルを置いておくとかいろいろなアイデアが
あります。処理系を作られる方はここで大いに悩んでください。この部分の設計が、そのシステムが
どんな問題に向いているかを決定してしまいます。
その他のオブジェクトの実装
このほかのデータ構造として挙げられるのは数値アトム、ストリング、ベクター、ストリームなどが
あるでしょうか。Lispはどんな構造のデータでも受け入れることのできるような強力で柔軟なデータ
構造を持っています。実際、例えばベクタがなくてもリストとして実現することができます。n進木
もリストに翻訳できます。シンボルに属性を与えるやり方として、LispではPLISTという方法があり
ます。ですが元々のデータ構造が問題に適したものであるかどうかはプログラムの(スピードに
於いてもメモリ使用量の面でも)効率に於いて極めて大きな影響を持ちます。なんでもリストに翻訳
して実装しなければならないようなデータ構造で効率が上がるとは言えません。今日非常にたくさん
のプログラミング言語が提案されて続々と増えている現状は、プログラミング言語に向き不向きが
あって問題に適しているかどうかが大きな要素であることを物語っているのではないでしょうか?
例えば、深層学習が脚光を浴びてきてPythonが隆盛になってきたように、新たな問題が登場する
たびに新たなプログラミング言語が求められます。次の世代に誇れるような立派なプログラミング
言語を開発して頂けたら望外の喜びです。
GCのためのデータ構造
もうお気づきでしょうが、GCの実装には、セルごとに、そのセルが使用中であることを示す1ビット
の記憶場所が必要になります。このビットは通常はオフになっていて、markingの時に、もし使用中
セルであればオンに、そうでなければオフのままでcollectionに移行して、回収すべきセルであるか
どうかを決定するのに参照され、再びオフにされます。ここで実は、逆転ポインタ法を実装する
ためには、セル毎にもう1ビットづつ記憶場所を用意する必要があります。それは、今実行中の
markingのフェイズがcarだったのかcdrだったのかによってrecursionから帰る帰り先を決定しな
ければならないからです。その時にこの1ビットの情報が不可欠になります。通常の再帰では、戻り
先の情報はスタックに積まれています。それを制限しているので、セルの中の1ビットをこれに割り
当てる必要が出てくるのです。ですが、セルの中に1ビットを忍び込ませるのと、スタックにいち
いち1ワードずつpushするのと、どちらがメモリを節約できるか、どちらが実行速度が上がるか、
という問題になります。MPLispの頃はメモリの節約が至上命題でした。今日では多分実行速度が
至上命題になるでしょう。逆転ポインタ法と再帰によるmarkingとどちらが早いかの判断は処理系
製作者の手に委ねられています。賢明な判断をお願い致します。私の考えでは、markingには逆転
ポインタ法を、collectionには線形化圧縮ガーベジコレクタを導入するのが実行速度を稼ぐのに有利
だと思っています。ですが私にはまだ線形化圧縮ガーベジコレクタを実装した経験がありません。
これを導入するためにはデータ構造を根本的に変更する必要が出てきます。処理系製作者の腕の
見せ所でしょう。
GCの処理の流れ
MPLispの制作にあたって、私はただ一点だけ恩師に教えを乞う必要がありました。それは、先ほど
rootと表現していた、markingの起点をどこにするか、という点です。先生は私が独力で開発しよう
としているのを買ってくださったのか、わざと、専門用語を使うことを避けて、しかも具体的な処理
の流れに言及せず、すぐ横にあった黒板も使用せずに説明してくださいました。そして「使用中の
データを捉えているデータ構造の起点がいくつもあるだろうから、それらをすべてを起点にして
データ構造を芋づる式に追いかけていけばmarkingが可能なはずだよ」と教えてくださいました。
私の誤解は、この起点がただの一か所であるという思い込みから起こったものでした。起点は
たくさんあります。スタックの各要素とか、シンボルの中で値や関数定義などを捉えている起点
からもセル領域にポインタが伸びています。これらすべてを起点にmarkingして必要なデータを捕捉
していきます。これには再帰と繰り返しの両方を使い分けて網羅する必要があります。使用中の
データのセルを誤って資源回収することのないようにコーディングする必要があります。
この辺りは結構細かい配慮が必要な部分ですので、慎重に事を進めてください。
GCの実装
ここで、コードじみたものを示してみますが、この記法は、M 式もどきで、M式とPL/IとBasic
その他諸々が混ざってしまっています。ご了承ください。
atom[tree]とあるのは、ポインタtreeの指すオブジェクトがatomであることを判断する述語です。
markedp[tree]とあるのはポインタtreeの指すセルがmarkされていることをテストする述語です。
mark-a-cell[tree]とあるのはtreeの指すセルにマークを付ける擬関数です。
mark-an-atom[tree]も同様、atomをmarkします。(symbolをmarkするのか?と思う方も
いらっしゃるでしょう。実はsymbolもmarkしなければならない場合があるのです。特に数値アトムは
markする必要があります。)
mark-a-tree<==λ[[tree];[atom[tree] ->mark-an-atom[tree];
markedp[tree]->nil;
t ->progn[mark-a-cell[tree];
mark-a-tree[car[tree]];
mark-a-tree[cdr[tree]]
] ] ].
これは逆転ポインタ法ではなく、recursionでGCのアルゴリズムを表現したものです。
このように書くと、情けないくらい簡単です。Lisperたる諸兄がこれを読みこなすのは容易い
でしょう。これを基に、制御の流れ(帰り先)だけをスタックに積んで変数の値を復元する操作を
逆転ポインタ法で実現すると、煩雑で手続き的な汚らしいコードになります。
なんだか記法がますますおかしくなっていますが、ご了承ください。
:=は代入を表します。Pascalでの記法です。car[PROCESSING]はポインタPROCESSINGの指す
セルのcar部分を表します。cdrも同様です。MPLispではセルを2つの配列car(x)、cdr(x)で
実装していました。その名残です。また、M式に於いて引数を区切るために使われる「;」と
コメントの始まりを示す(S式の)「;」 がごっちゃに使われていますので混同しないように
してください。progn[form1,form2,...,formn]はform1からformnをこの順で実行すること
を示します。(現代のLispでは明示的には書かれません。)
;逆転ポインタ法:制御の流れの決定にだけスタックを利用して実装。
defglobal[ROOT;PROCESSING;NEXTTARGET]
;
;ROOTがmarkすべき二進木を指しているobject(root)を指していて、
; PROCESSINGがmarkすべき二進木を指しているものとする。
;
mark-a-tree<==λ[[];
[atom[PROCESSING] ->mark-an-atom[PROCESSING];
markedp[PROCESSING]
->nil; ;PROCESSINGの指すcellがマーク済みなら
; 何もしない。
t ->progn[ ;
mark-a-cell[PROCESSING]; ;
NEXTTARGET:=car[PROCESSING]; ;次のネスティングレベルで、
; PROCESSINGの指すcellのcarの指す
; cellをmarkずる準備。
ROOT:=PROCESSING; ;次のネスティングレベルでは
; PROCESSINGの指すcellが
; (新たな)rootとなる。
car[PROCESSING]:=ROOT; ;ポインタをひっくり返しておく。
; 即ち、PROCESSINGのさすcellのcarに
; (元の)rootを指させる。
PROCESSING:=NEXTTARGET; ;次のネスティングレベルでは
; PROCESSINGの指すcellの
; carのさすcellが
; (新たな)markの対象になる。
mark-a-tree[]; ;戻り先だけstackに積んでrecursion。
NEXTTARGET:=PROCESSING; ;ひっくり返したcarを復元する準備。
PROCESSING:=ROOT; ;汎用レジスタPROCESSINGの復元。
ROOT:=car[PROCESSING]; ;ひっくり返したcarから汎用レジスタROOTの
; 復元:ROOTは一旦rootを向く。
car[PROCESSING]:=NEXTTARGET; ;ひっくり返したcarの復元。
NEXTTARGET:=cdr[PROCESSING]; ;次のネスティングレベルで、
; PROCESSINGの指すcellの
; cdrの指すcellをmarkする準備。
ROOT:=PROCESSING; ;次のネスティングレベルでは
; PROCESSINGの指すcellが
; (新たな)rootとなる。
cdr[PROCESSING]:=ROOT; ;ポインタをひっくり返しておく。
; 即ち、PROCESSINGの指すcellのcdrに
; (元の)rootを指させる。
PROCESSING:=NEXTTARGET; ;次のネスティングレベルでは
; PROCESSINGの指すcellのcdrの指す
; cellが(新たな)markの対象になる。
mark-a-tree[]; ;戻り先だけstackに積んでrecursion。
NEXTTARGET:=PROCESSING; ;ひっくり返したcdrを復元する準備。
PROCESSING:=ROOT; ;汎用レジスタPROCESSINGの復元。
ROOT:=cdr[POCESSING]; ;ひっくり返したcdrから
; 汎用レジスタROOTの復元
; これでROOTは再びrootを向く。
cdr[PROCESSING]:=NEXTTARGET; ;ひっくり返したcdrの復元。
;NEXTTARGETを復元する必要はない。
]
] ].
このコードに於いて、いくつか注意点を挙げておきます。
1.このコードをデバッグするための時間は残されていませんでした。時間の使い方が下手だったためです。
それ故、このコードにはバグがたくさん含まれていることがほぼ確実です。
特に、コード中に書いたコメントと図解の同期が取れていない部分がかなりあるようですが、
修正する時間がありません。その点を考慮に入れてご利用ください。
2.このコードをどのように利用されても構いません。転載、引用、改変も自由です。
このコードを何らかのプログラミング言語に移植して利用することも制限いたしません。
ただ、私自身がこのコードの著作権を放棄するわけではありません。
また、このコードを利用して何らかの不具合や不利益が発生しても、私は一切の責任を負いません。
あくまで自己責任100%でお願いいたします。
3.このコード、およびこの記事についてご批判、お𠮟り、感想等どしどしお寄せください。
リプライ大歓迎です。寄せてくださったら泣いて喜びます。
このコードは、まだスタックを一部に用いているのですが、まったく用いないで書くと
次にようになります。
;逆転ポインタ法:スタックを用いていない。
defglobal[ROOT;PROCESSING;NEXTTARGET;GRANDROOT]
;
;ROOTがmarkすべき二進木を指しているobject(root)を指していて、
; PROCESSINGがmarkすべき二進木を指しているものとする。
;GRANDROOTはmarkingの元々の起点を示したままである。
;
mark-a-tree<==λ[[];
label[0];
[atom[PROCESSING] ->mark-an-atom[PROCESSING];
markedp[PROCESSING]
->nil; ;PROCESSINGの指すcellがマーク済みなら
; 何もしない。
t ->progn[ ;
mark-a-cell[PROCESSING]; ;(図ステップ1)
NEXTTARGET:=car[PROCESSING]; ;次のネスティングレベルで、
; PROCESSINGの指すcell
; (図ステップ1のセル1)
; のcarの指すcell(obj1)を
; markずる準備。
car[PROCESSING]:=ROOT; ;ポインタをひっくり返しておく。(図ステップ2)
; 即ち、PROCESSINGのさすcellのcarに
; (元の)rootを指させる。
; (図ステップ2つけかえ1)
PROCESSING:=NEXTTARGET; ;次のネスティングレベルでは
; NEXTTARGET(図ステップ2)
; のさすcell(obj3)が
; (新たな)markの対象になる。
; (図ステップ2つけかえ2)
a_or_d[PROCESSING]:=true; ;a_or_dは、carをmarkしている時はtrue、
; cdrをmarkしている時はfalseで、
; cdr部分に付随した1bitのフラグ。
goto[0]; ;recursion的な意味合いのgoto文
label[1]; ;recursionから戻ってくるポイント1
NEXTTARGET:=PROCESSING; ;ひっくり返したcarを復元する準備。
PROCESSING:=ROOT; ;汎用レジスタPROCESSINGの復元。
ROOT:=car[PROCESSING]; ;ひっくり返したcarから
; 汎用レジスタROOTの復元
; (図ステップ3つけかえ1)
; ROOTは一旦rootを向く。
car[PROCESSING]:=NEXTTARGET; ;ひっくり返したcarの復元。
;ここから先は、cdr部分の為のコードであり、car部分の為のコードとそっくりですので注釈は簡略化いたします。
NEXTTARGET:=cdr[PROCESSING]; ;次のネスティングレベルで、
; PROCESSINGの指すcell(セル1)の
; cdrの指すcell(obj2)をmarkする準備。
cdr[PROCESSING]:=ROOT; ;ポインタをひっくり返しておく。
; 即ち、PROCESSINGの指すcellのcdrに
; (元の)rootを指させる。
PROCESSING:=NEXTTARGET; ;次のネスティングレベルでは
; NEXTTARGETの指すcell(obj2)
; が(新たな)markの対象になる。
goto[0]; ;recursion的な意味合いのgoto文
label[2] ;recursionから戻ってくるポイント2。
NEXTTARGET:=PROCESSING; ;ひっくり返したcdrを復元する準備
PROCESSING:=ROOT; ;汎用レジスタPROCESSINGの復元。
ROOT:=cdr[PROCESSING]; ;ひっくり返したcdrから
; 汎用レジスタROOTの復元
; これでROOTは再びrootを向く。
cdr[PROCESSING]:=NEXTTARGET; ;ひっくり返したcdrの復元。
;NEXTTARGETを復元する必要はない。
[a_or_d[processing]->goto[1]; ;return文の代わりにgoto。
; cdr部のmarkに移る。
t->[equal[PROCESSING;
GRANDROOT]->GOTO[3];;このGRANDROOTでのmarkingを終える為に3に飛ぶ。
t-> goto[2] ;cdr部分のmarkを終える為にrecursionから2に戻る
]
label[3] ;このGRANDROOTでのmarking全て終わり。
]
] ].
このコードに於いても1.2.3.の注意点は同じです。
goto文を用いるために、progが明示的に出てきます。それ以外にはprog形式の意味は
ありません。
markingのフェイズを判定するために、a_or_d[PROCESSING]という、cdr部分に付随した
1ビットの変数を用いています。これにtrueかfalseを代入しておいてフェイズを判定する、
という言う次第です。これともう一つ、GRANDROOTという、markingの起点を示す
ポインタを用いています。これは多分メモリ上の一定のアドレスに置かれるべき変数で、
その起点についてのmarkingを終えたかどうかの判定に用いられます。
GRANDROOTはa_or_d[PROCESSING]と違ってシステムの中でただ一つです。
このa_or_dとGRANDROOTを導入したことによって帰り先をスタックに積まずに
recursionから戻ることができるのです。
或いは、スタックを使わずに済むようにするだけの為にコードを複雑にしすぎたかもしれません。
もしメモリの節約がスピードの向上に役立たないようであれば、強引に逆転ポインタ法を
導入する今日的な意義はなくなってしまうでしょう。スタック領域を十分にとってスタック
オーバーフローを防げるようなアプリケーションであればいじましくスタックを節約する
意義はないからです。しかも64ビットCPUの導入によって、スタック操作に必要な時間も
少なくて済むようになっているかもしれません。
今回コードを再現する試みによってようやく気付いたことなのですが、私は「逆転ポインタ法
さえ導入すれば循環リストに攪乱されずに動作するGCが実現する」と思い込んでいました。
実際はrecursionで書いても循環リストに攪乱されないGCが書けるし、逆転ポインタ法を導入
しても循環リスト問題が自動的に解決するものではないことがわかりました。
また、諸兄に残された課題はまだあります。それはequalとprintです。ここではその実装に
触れるつもりはありませんが、循環リストによって攪乱されてしまうのがGCのほかにequalと
printです。システムによってはほかにも(copyなど)あるかもしれません。循環リストに攪乱されない
GC、print、equalをぜひ実装してみてください。
結び:スタック無し再帰について
私がMPLispを作ったころ、前述したようにメモリの節約は重大な問題でした。そこで開発
したのが「スタック無し再帰」です。その意義は今日失われてしまったかもしれませんが、
Lisp処理系が再帰を内部でどうやって実現しているか、について考察する教材としての
意義は失われていないと思っています。ここで具体的な実装法について述べる時間はもう
ありませんが、有名なハノイの塔の問題はかなり簡単にスタック無し再帰を実現できる
練習問題ですので、再帰を実現する方法がイマイチ解らないと仰る方は解いてみてください。
私がここで具体的な話をウダウダ書くより実験してみるほうがはるかに早く身に付きます。
念のために、この記事の末尾にヒントを載せておきます。自信のない方だけ参照してください。
中西先生の本に載っている「アッカーマン関数」は、再帰に頼っている限り現実的な時間内に
解く見込みのまったくない問題です。私はこれをスタック無し再帰に書き直してFORTRANで
実行してみたことがあります。結果は無残なものでした。メインフレームを1時間も独占して
稼働させてもAck(4,3)が求まらないのです。しかしテーブルを作りながら解いていけば手計算
で求められることがわかりました。コンピュータでも、テーブルルックアップによって瞬時に
解くことができますので、ご興味のある方はやってみてください。recursionを諦めれば実行
速度を飛躍的に高められるといういい例です。因みに、私はアッカーマン関数の一般項を求めて、
数学的帰納法でそれを証明することにも成功しました。なお、メインフレームを1時間独占して
その間に得られたトータルCPUタイムは約20分でした。OSが残りの40分間何をやっていたのかは
謎です。メインフレームというのは大勢でいっぺんに利用することには強くても、PCのように
一人で独占して使うことには不向きなのかもしれませんね。
付録・ハノイの塔をスタック無し再帰で書くためのヒント
穴の開いた円盤がn枚あります。一番小さい円盤が1番です。円盤を挿して置いておくことの
できる場所A,B,Cがあります。Bを使って円盤をAからCに移せ、という例の問題です。
recursionを使えばすぐに解けますね。ここで、「recursionのネスティングレベルが高まるとき、
そして下がるとき、に円盤の番号は1づつデクリメント/インクリメントされます。
そしてA,B,Cが一定の方法でシャッフルされます。この間、失われる情報はありません。」これがヒントです。
参考文献
1.Lisp入門 第2版 中西 正和 著 近代科学社
2.はじめてのLisp関数型プログラミング 五味 弘 著 技術評論社
3.M言語:Lispの源流を訪ねて 笹川 賢一 著 Kindle版 Amazon.co.jp