【競技プログラミング】中国人郵便配達問題をやってみた【組合せ最適化】

1.初めに

・アルゴリズムを学ぶために、競技プログラミングを始めました。
・AOJのコースをやっていくので、その備忘録を残します。

・前回は巡回セールスマン問題を解いたので、今回は「中国人郵便配達問題」を解いていきます。

2.中国人郵便配達問題

2.1問題

重み付き無向グラフ $G(V,E)$ について、以下の条件を満たす最短経路の距離を求めて下さい：

• ある頂点から出発し、出発点へ戻る閉路である。
• 各辺をちょうど１度通る。

入力

$|V|$ , $|E|$ はそれぞれグラフ $G$ の頂点の数と辺の数を示す。グラフ $G$ の頂点にはそれぞれ $0, 1, ..., |V|-1$ の番号が付けられている。

$s_i$, $t_i$ はグラフ $G$ の $i$ 番目の辺が結ぶ２つの頂点を表す（無向）。$d_i$ は $s_i$ と $t_i$ の間の距離　（$i$ 番目の辺の重み）である。グラフ $G$ には多重辺が含まれる場合がある。

出力

最短経路の距離を1行に出力する。

制約

• $2 ≤ |V| ≤ 15$
• $0 ≤ |E| ≤ 1,000$
• $0 ≤ d_i ≤ 1,000$
• $s_i ≠ t_i$
• グラフ$G$ は連結である

3. 問題の考え方

・中国人郵便配達問題は、無効グラフの図が「一筆書きで描ける場合」と「一筆書きで描けない場合」で解法が変わります。

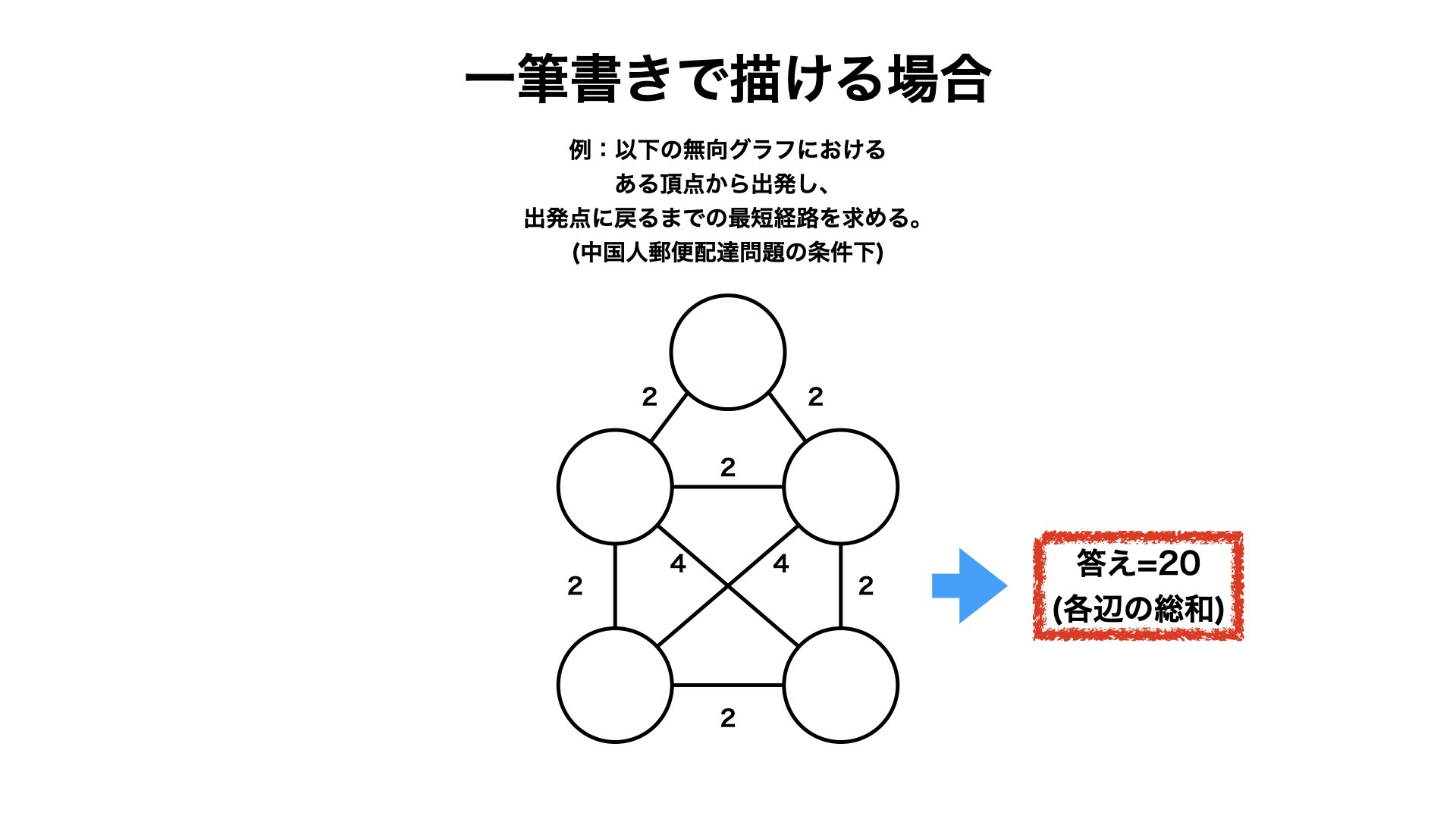
3.1. 一筆書きで描ける場合

・一筆書きで描ける場合は「各辺の総和」が答えとなります。(各辺をちょうど一度通るという条件より)

・下の入力例で考えてみます。

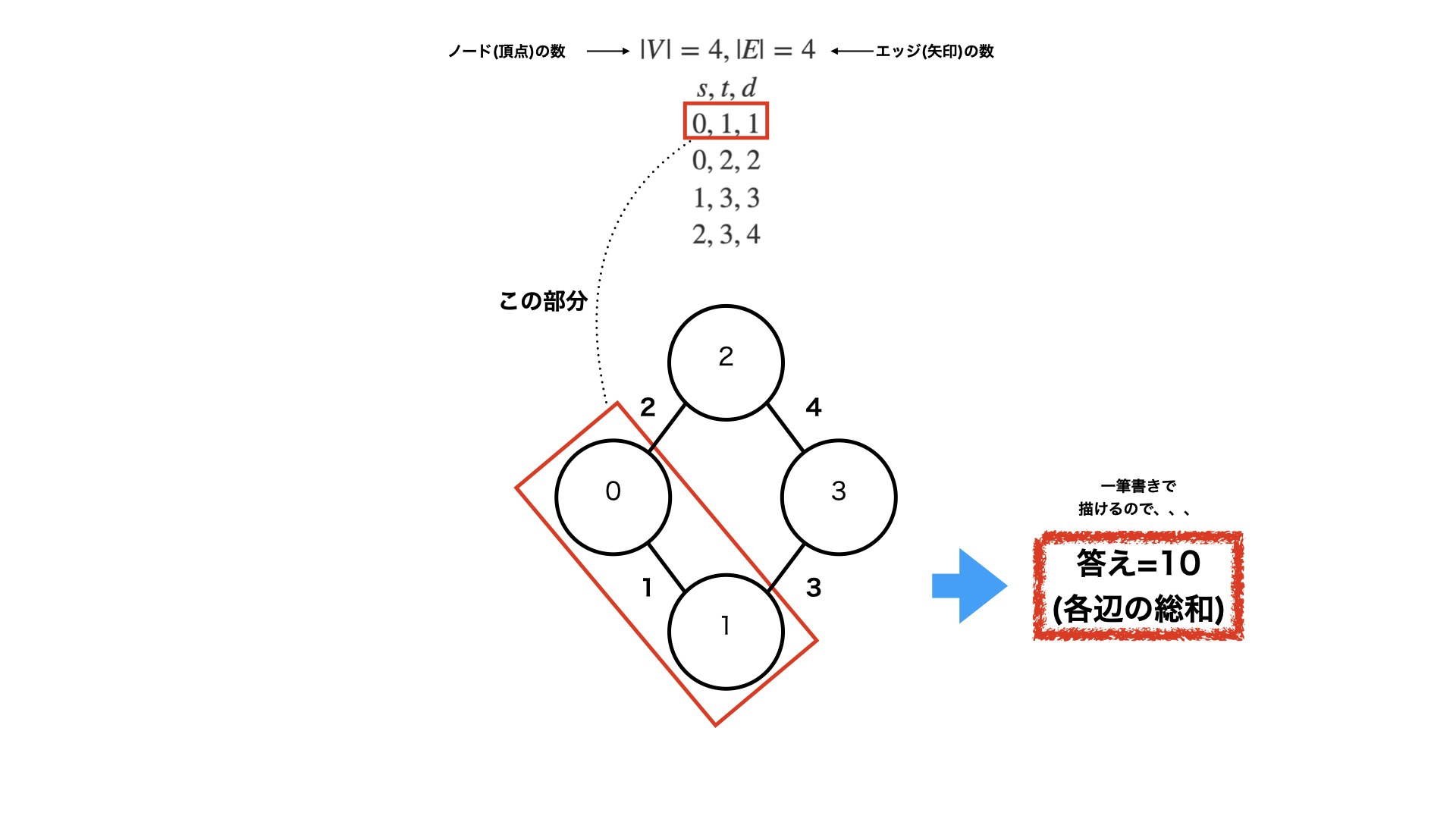
4 4
0 1 1
0 2 2
1 3 3
2 3 4

　　　　　　 　　　　　　 　　　　　　　　　 ↓　つまり

|V|=4,|E|=4
\\
\\
s,t,d\\
0,1,1\\
0,2,2\\
1,3,3\\
2,3,4\\
(d:sからtまでの距離)

・これを図で書いてみます。

・一筆書きで描ける場合は非常に簡単なので、次の一筆書きで描けない場合に全部フォーカスします。

3.2. 一筆書きで描けない場合

・一筆書きで描ける場合は「各辺の総和」+「次数が奇数の頂点で作成した完全グラフにおける完全マッチングの最小経路」←??????????????が答えとなります。

・「次数が奇数の頂点で作成した完全グラフにおける完全マッチングの最小経路」が意味がわからないので、一つずつみていきます。

・まず、「次数が奇数の頂点」を取り出します。

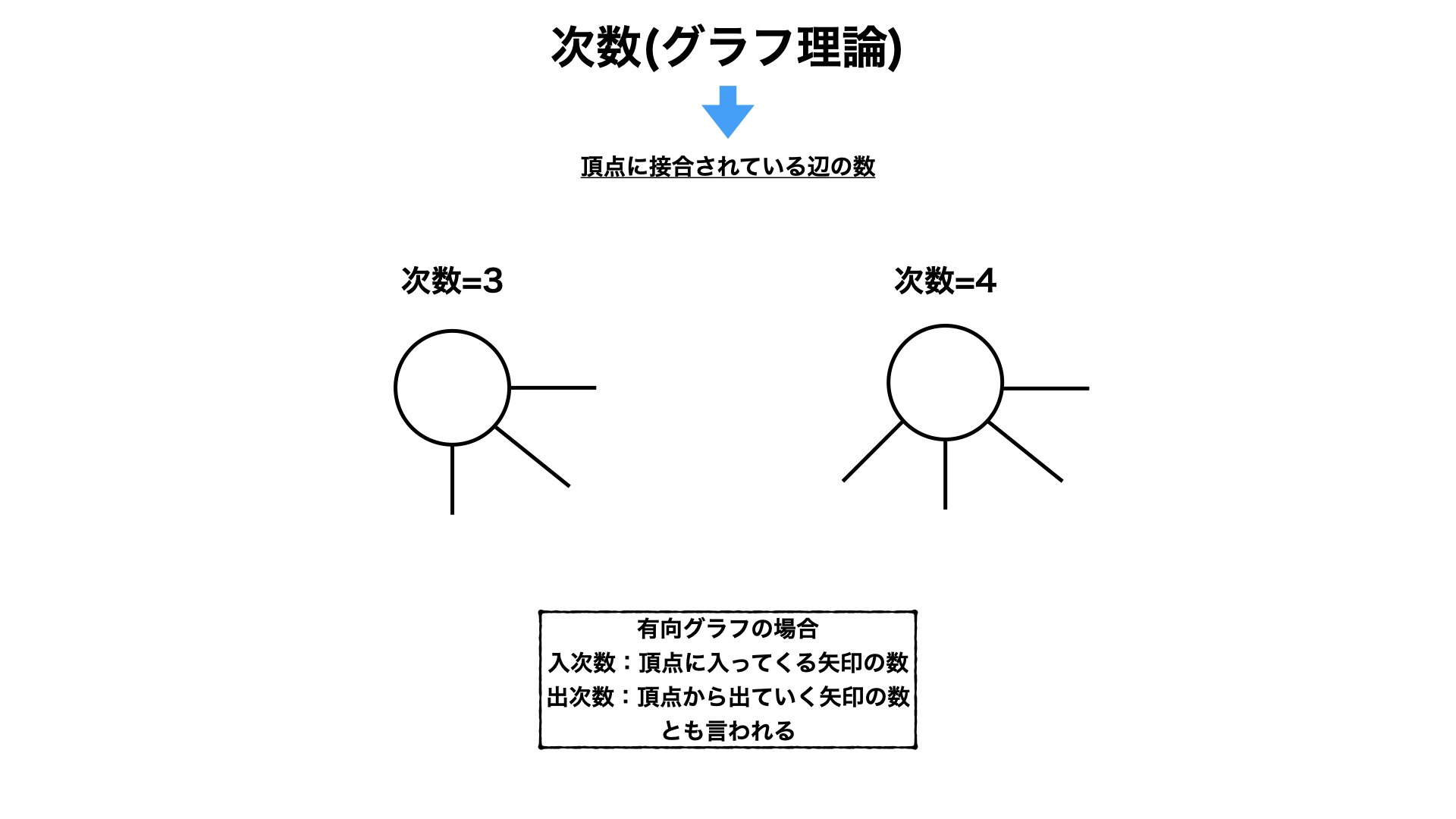
3.2.1. 次数って何？

頂点に接合されている辺の数

・取り出した「次数が奇数の頂点」を使って「完全グラフ」を作ります。

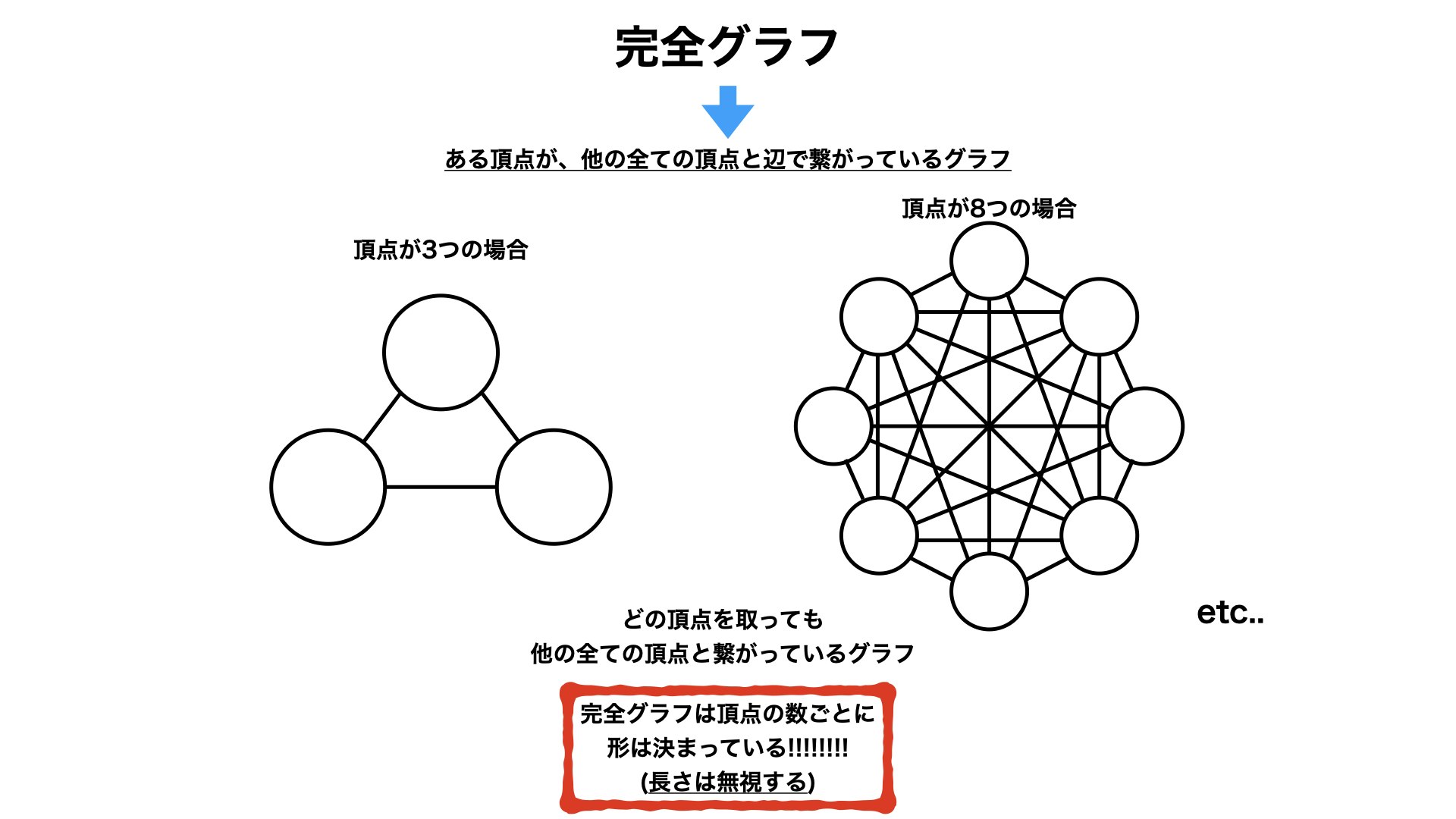
3.2.2. 完全グラフって何？

ある頂点が、他の全ての頂点と辺で繋がっているグラフ

・作った「完全グラフ」から、経路の合計が最小となる「完全マッチング」を見つけます。

・この完全マッチングの最小経路と元のグラフの各辺の総和が求める答えとなリます。

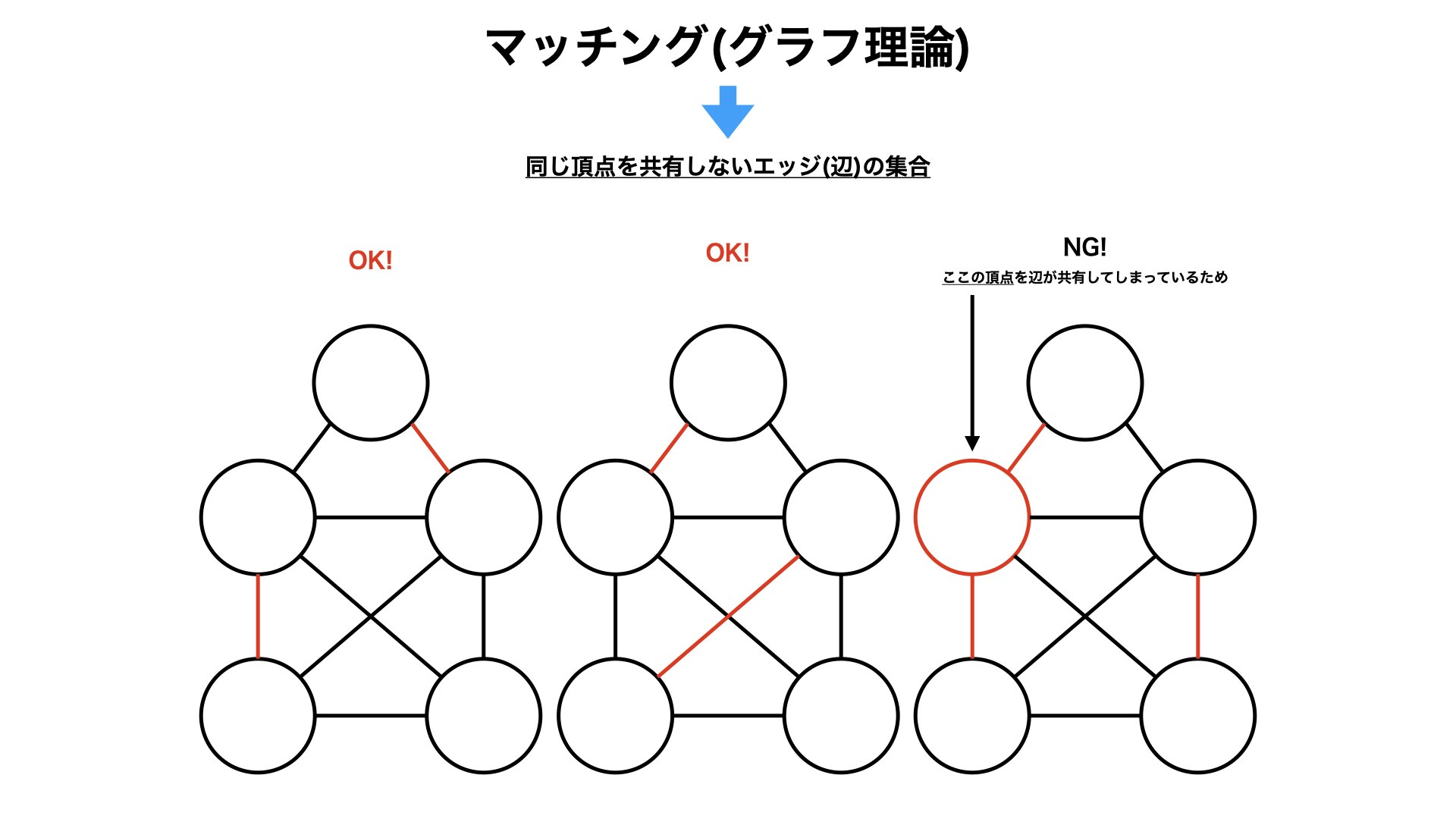
3.2.3. マッチングって何？

同じ頂点を共有しないエッジ(辺)の集合

・言葉よりも図を見た方が理解できると思われます。↓

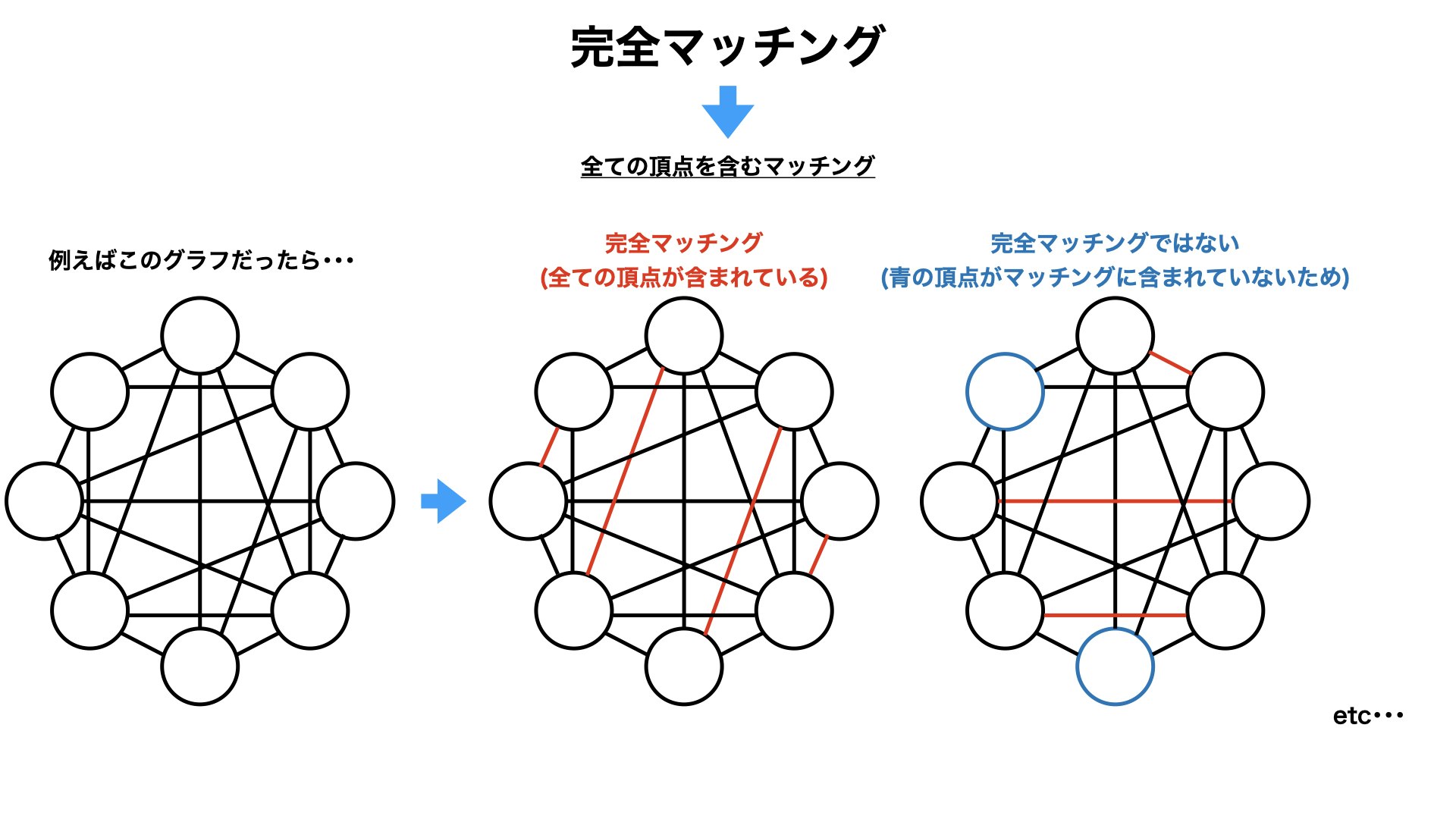
3.2.4. 完全マッチングって何？

全ての頂点を含むマッチング

3.2.5. 一筆書きで描けない場合の解き方まとめ

「次数が奇数の頂点を取り出す」
　　　　　　 ↓　
「取り出した頂点で完全グラフを作る」
　　　　　　 ↓　
「作った完全グラフで経路が最小となる完全マッチングを取り出す」
　　　　　　 ↓　
「元の図の全辺の総和+完全マッチングの最小経路を求める」

・この三つの手順が、「一筆書きで描けない場合」の答えの導き方です!!!!!!!!

4. 例題

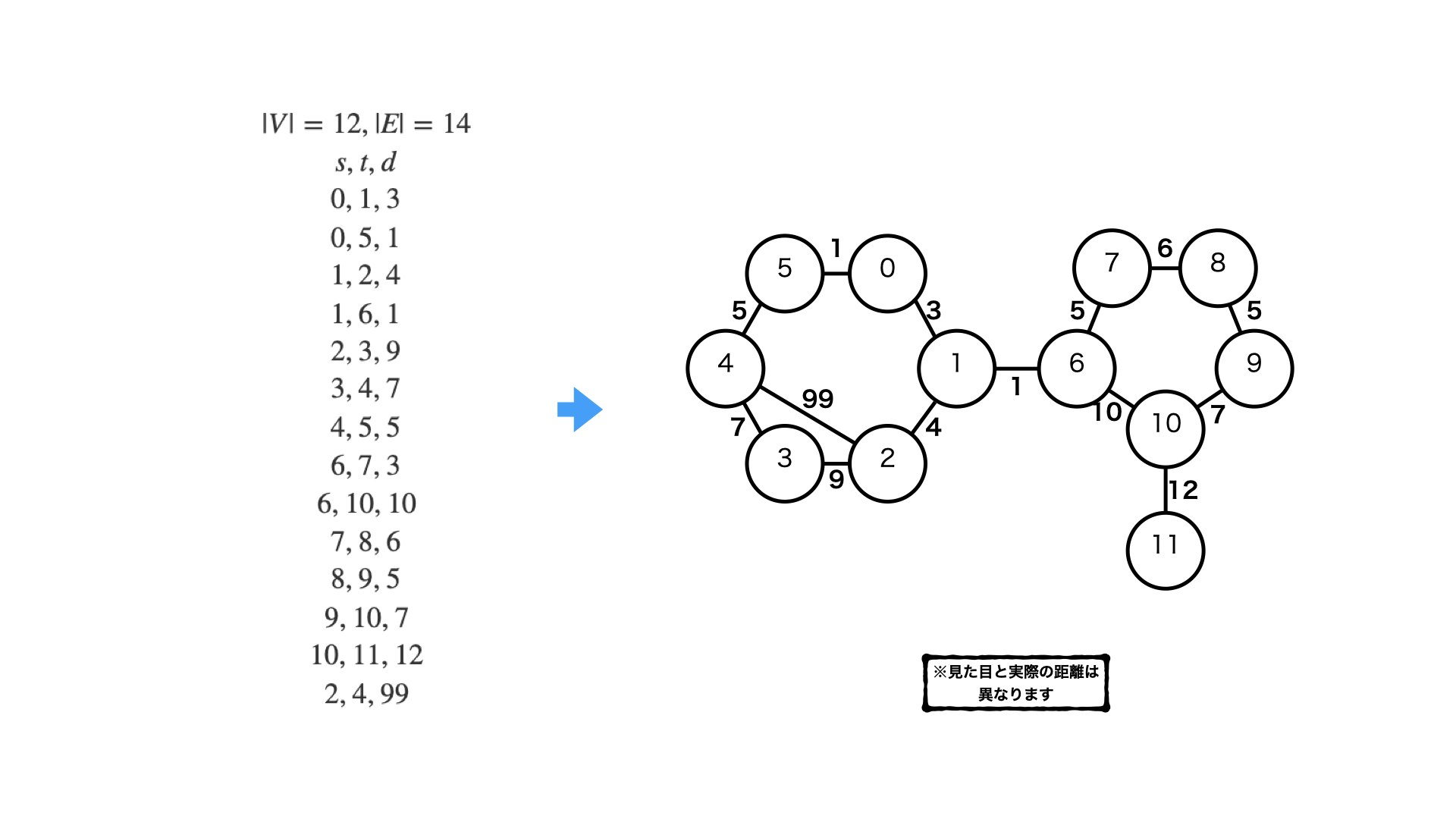
・下の入力例を元に考えてみます。

12 14
0 1 3
0 5 1
1 2 4
1 6 1
2 3 9
3 4 7
4 5 5
6 7 3
6 10 10
7 8 6
8 9 5
9 10 7
10 11 12
2 4 99

　　　　　　 　　　　　　 　　　　　　　　　 ↓　つまり

|V|=12,|E|=14
\\
\\
s,t,d\\
0 ,1 ,3\\
0 ,5 ,1\\
1 ,2 ,4\\
1 ,6 ,1\\
2 ,3 ,9\\
3 ,4 ,7\\
4 ,5 ,5\\
6 ,7 ,3\\
6 ,10 ,10\\
7 ,8 ,6\\
8 ,9 ,5\\
9 ,10 ,7\\
10 ,11 ,12\\
2 ,4 ,99\\
(d:sからtまでの距離)

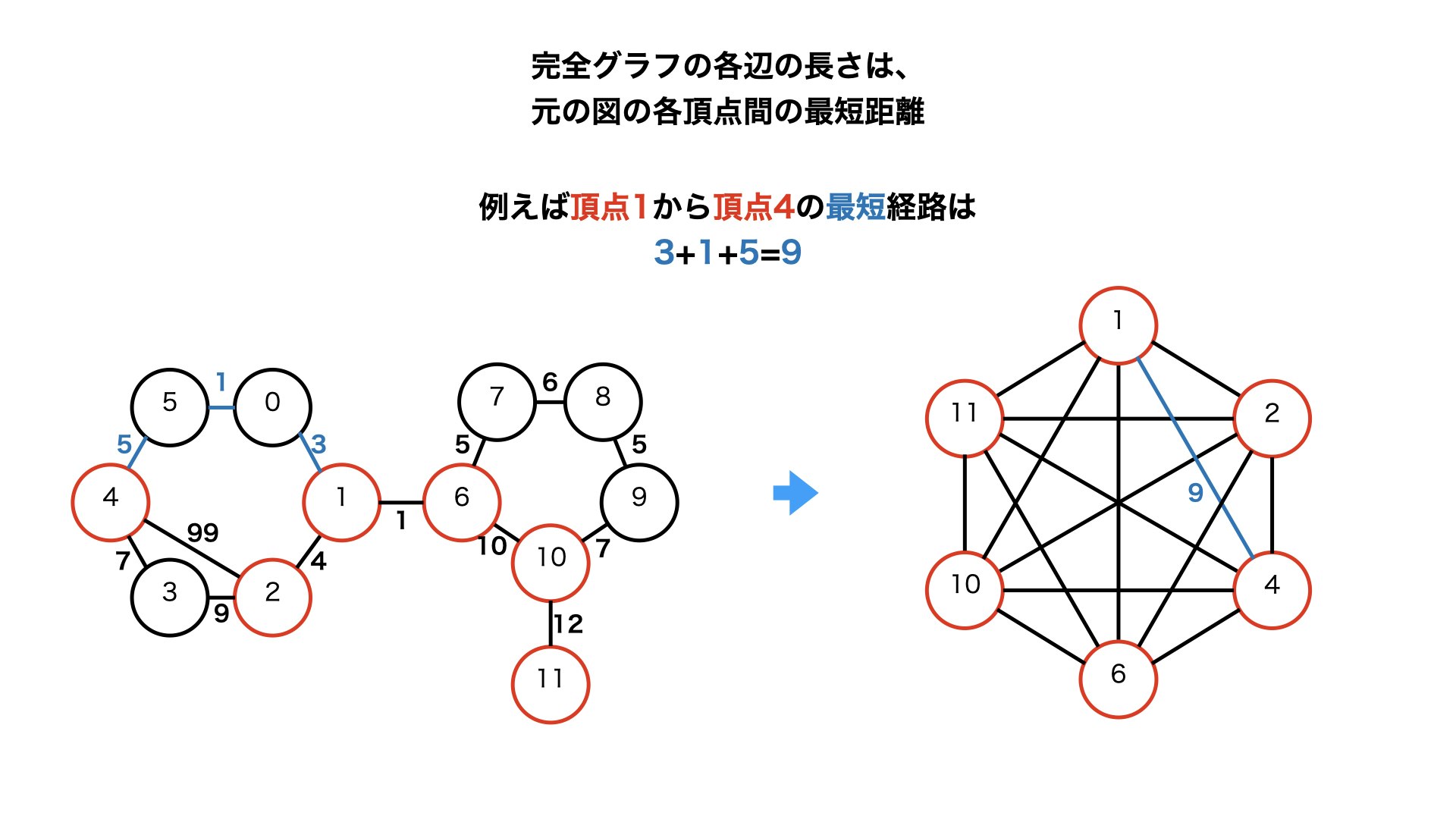
・これを図で描いてみます。(普通は書きませんが、分かりやすさを出すために描きます)

・このグラフは一筆書きでは描けないので、以下の手順にしたがって解いていきます。

「次数が奇数の頂点を取り出す」
　　　　　　 ↓　
「取り出した頂点で完全グラフを作る」
　　　　　　 ↓　
「作った完全グラフで経路が最小となる完全マッチングを取り出す」
　　　　　　 ↓　
「元の図の全辺の総和+完全マッチングの最小経路を求める」

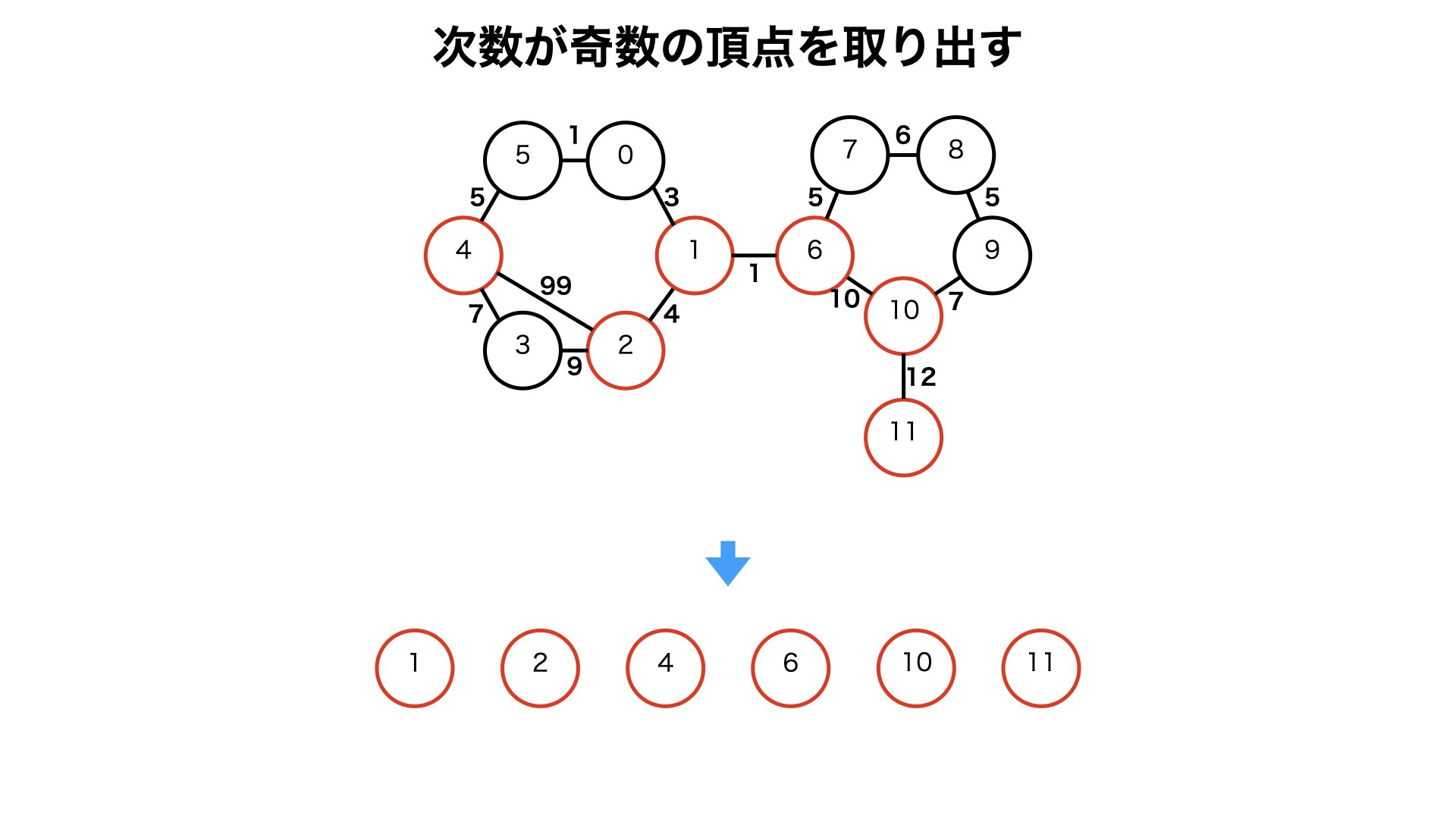
4.1. 次数が奇数の頂点を取り出す

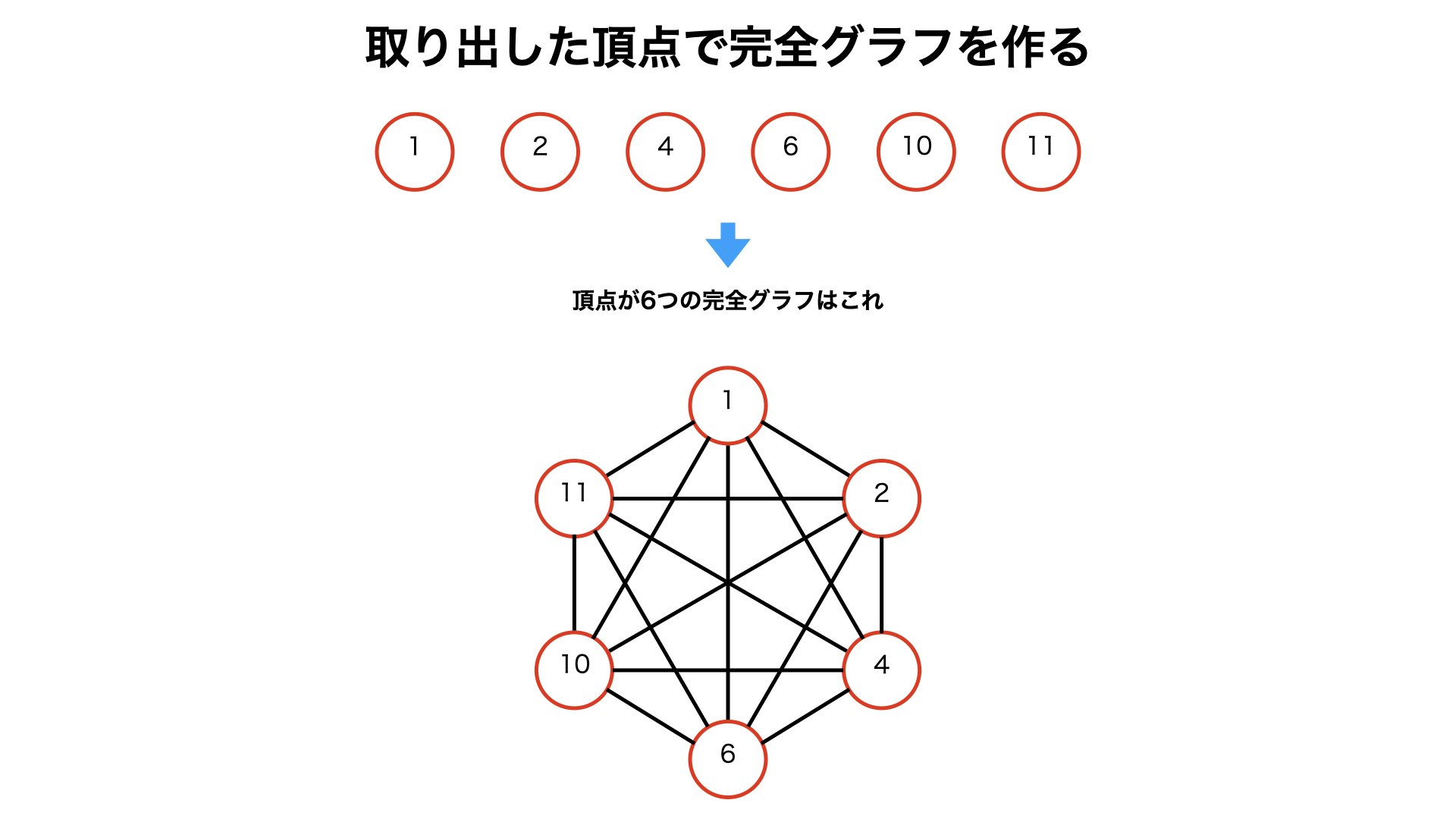
・このグラフでは「次数が奇数の頂点」は「1,2,4,6,10,11」の六つです。

4.2. 取り出した頂点で完全グラフを作る

・頂点が六つの完全グラフは以下のようになります。

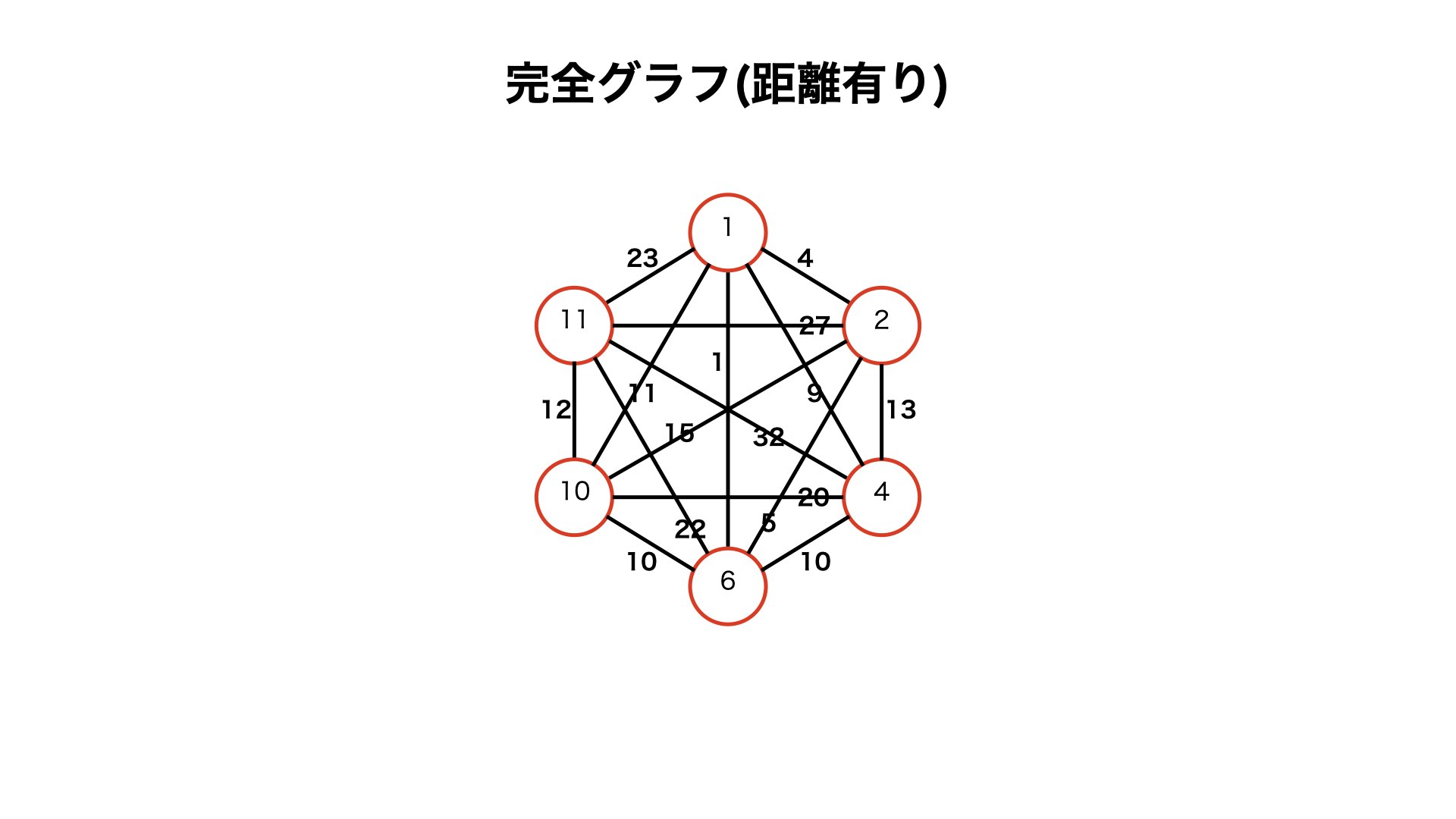
・作成した完全グラフの各経路の距離は、「元のグラフの頂点間の最短経路」となります。

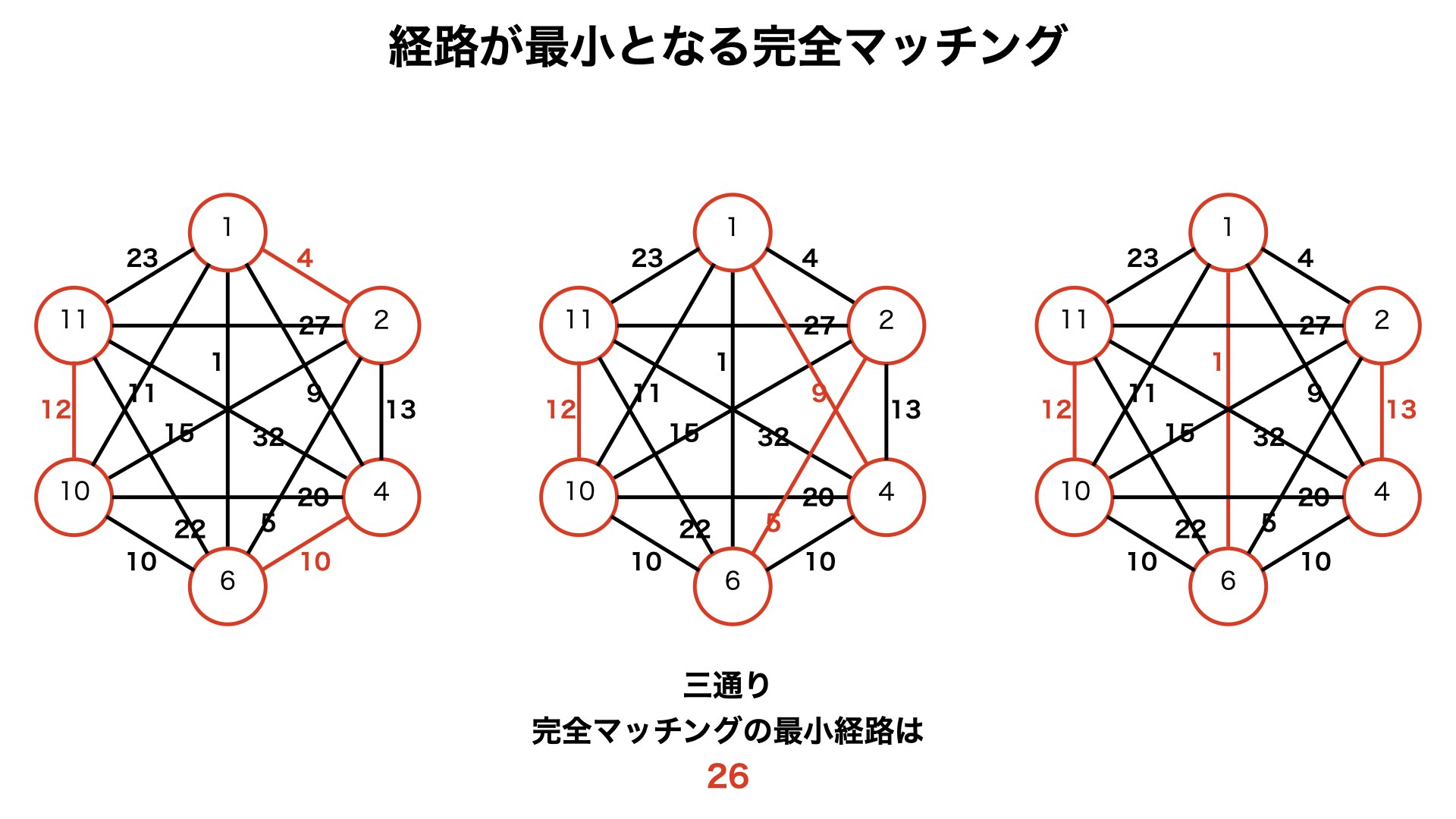
4.3. 作った完全グラフで経路が最小となる完全マッチングを取り出す

・経路が最小の完全マッチングは三通りあります。

・最小経路は26です。

4.4. 全辺の総和+完全マッチングの最小経路を求める

・元の図の全辺の総和+完全マッチングの最小経路=172+26=198が求める答えとなります。

５.　実装

# 入力値取得
V,E=map(int,input().split())

# 隣接行列Aの作成
inf=float("inf")
A=[[inf]*V for _ in range(V)]

# 頂点の次数リストDの作成
D=[0]*V

# 隣接行列Aの要素を埋める。次数リストDを埋める。各辺の総和ansを求める
ans=0
for _ in range(E):
    s,t,d=map(int,input().split())
    A[s][t]=min(A[s][t],d)
    A[t][s]=min(A[t][s],d)
    D[s]+=1
    D[t]+=1
    ans+=d
    
for i in range(V):
    A[i][i]=0
for k in range(V):
    for i in range(V):
        for j in range(V):
            A[i][j]=min(A[i][j],A[i][k]+A[k][j])    
      
# 次数が奇数の頂点をリスト化
odd_lst = [x for x in range(V) if D[x] % 2]
    
# 完全マッチングの最小経路を求める
n = len(odd_lst)
dp = [inf]*(2**n)
dp[0] = 0
for i in range(2**n):
    for j1 in range(n):
        for j2 in range(n):
            if not i>>j1 & 1 and not i>>j2 & 1 and not j1 == j2 and not A[odd_lst[j1]][odd_lst[j2]] == inf:
                new_i = i|(1<<j1)|(1<<j2)
                dp[new_i] = min(dp[new_i], dp[i]+A[odd_lst[j1]][odd_lst[j2]])
                     
print(dp[-1]+ans)

5.1. 隣接行列Aについて

・経路を求める際に、「どの頂点とどの頂点が辺で繋がっていて、その距離はどのくらいあるのか」を明確にしておく必要があります。

・例題で用いた入力例で見てみると下記のような隣接行列Aが作れます。(空欄はinfで埋められています)

i\j	0	1	2	3	4	5	6	7	8	9	10	11
0	inf	3	inf	inf	inf	1	inf	inf	inf	inf	inf	inf
1	3		4				1
2		4		9	99
3			9		7
4			99	7		5
5	1				5
6		1						3			10
7							3		6
8								6		5
9									5		7
10							10			7		12
11											12

・無効グラフなので、隣接行列Aは対象行列となります。

・上の隣接行列について、さらに各頂点の最短距離で要素を更新していきます。

i\j	0	1	2	3	4	5	6	7	8	9	10	11
0	0	3	7	13	6	1	4	7	13	18	14	26
1	3	0	4	13	9	4	1	4	10	15	11	23
2	7	4	0	9	13	8	5	8	14	19	15	27
3	13	13	9	0	7	12	14	17	23	28	24	36
4	6	9	13	7	0	5	10	13	19	24	20	32
5	1	4	8	12	5	0	5	8	14	19	15	27
6	4	1	5	14	10	5	0	3	9	14	10	22
7	7	4	8	17	13	8	3	0	6	11	13	25
8	13	10	14	23	19	14	9	6	0	5	12	24
9	18	15	19	28	24	19	14	11	5	0	7	19
10	14	11	15	24	20	15	10	13	12	7	0	12
11	26	23	27	36	32	27	22	25	24	19	12	0

5.2. 次数リストDと次数が奇数の頂点リストKについて

・各頂点の次数を表したリストDは以下のようになっています。

頂点番号	0	1	2	3	4	5	6	7	8	9	10	11
次数	2	3	3	2	3	2	3	2	2	2	3	1

・次数が奇数の頂点は「1,2,4,6,10,11」となっています。

・なので次数が奇数の頂点リストKは以下のようになっています。

インデックス	0	1	2	3	4	5
次数が奇数の頂点	1	2	4	6	10	11

5.3. 完全マッチングの最小経路について

5.3.1. dp表の作成

・前回の巡回セールスマン問題と似た感じで、「bit列」と「頂点の集合」を対応させて以下のようなdp表を作ります。

(次数が奇数の)頂点集合 i	0	1	2	3	4	5	･･･	63
(次数が奇数の)頂点集合　bit列	000000	000001	000010	000011	000100	000101	･･･	111111
dp[new_i]	0	inf	inf	4	inf	9	･･･	26

・dp表の埋め方は以下のコードの通りです。

for i in range(2**n):
    for j1 in range(n):
        for j2 in range(n):
            if not i>>j1 & 1 and not i>>j2 & 1 and not j1 == j2 and not A[odd_lst[j1]][odd_lst[j2]] == inf:
                new_i = i|(1<<j1)|(1<<j2)
                dp[new_i] = min(dp[new_i], dp[i]+A[odd_lst[j1]][odd_lst[j2]])

i：次数が奇数の頂点集合
j1：移動後の頂点のインデックス
j2：移動前の頂点のインデックス

not i>>j1 & 1：移動後の頂点のインデックスj1は次数が奇数の頂点集合iに含まれない
not i>>j2 & 1：移動前の頂点のインデックスj2は次数が奇数の頂点集合iに含まれない

インデックス	0	1	2	3	4	5
次数が奇数の頂点	1	2	4	6	10	11

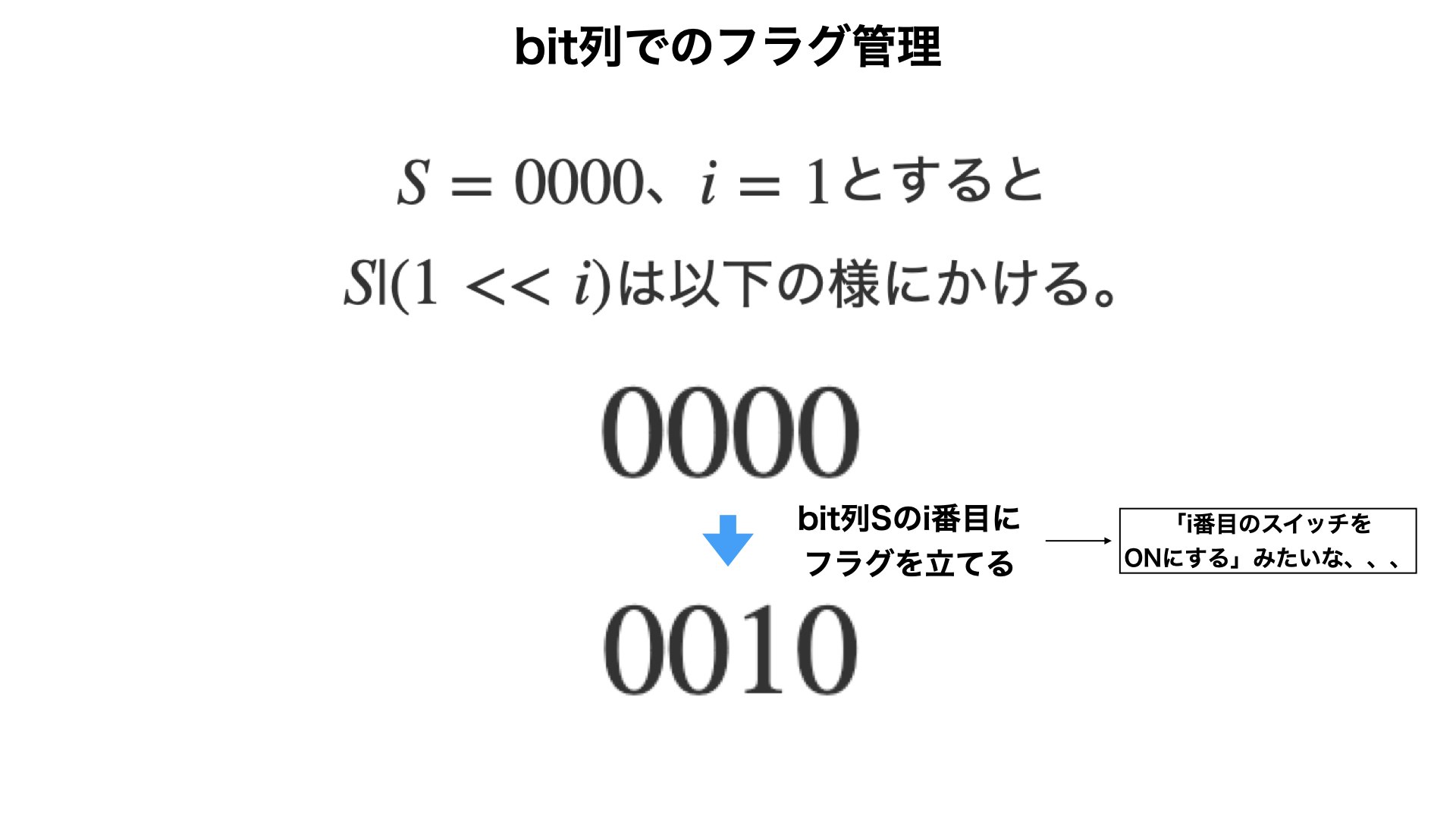
5.3.2. フラグ管理

・ビット列の計算ではフラグ管理というものがあります。

5.3.3. new_i = i|(1<<j1)|(1<<j2)について

・new_i=i|(1<<j1)|(1<<j2)は、「iのj1桁目とj2桁目にフラグを立てたもの」という意味になります。

・例えば$i=0、j1=0、j2=2$の場合、「ビット列000000の0桁目と2桁目にフラグを立てる」という意味になります。

・つまり、new_i=0000101となります。

・つまり、dp[new_i] = min(dp[new_i], dp[i]+A[odd_lst[j1]][odd_lst[j2]])で
dp[i]=0、A[odd_lst[j1]][odd_lst[j2]]=9なので、dp[new_i]=9となります。

(次数が奇数の)頂点集合 i	0	1	2	3	4	5	･･･	63
(次数が奇数の)頂点集合　bit列	000000	000001	000010	000011	000100	000101	･･･	111111
dp[new_i]	0	inf	inf	4	inf	9	･･･	inf

・その様にしてdp表を埋めると、 $i=63(ビット列111111)$のとき、dp[new_i]=26となります。

(次数が奇数の)頂点集合 i	0	1	2	3	4	5	･･･	63
(次数が奇数の)頂点集合　bit列	000000	000001	000010	000011	000100	000101	･･･	111111
dp[new_i]	0	inf	inf	4	inf	9	･･･	26