1.初めに
・アルゴリズムを学ぶために、競技プログラミングを始めました。
・AOJのコースをやっていくので、その備忘録を残します。
・前回は0-1ナップサック問題Ⅱを解いたので、今回は「個数制限付きナップサック問題」を解いていきます。
2.個数制限付きナップサック問題
2.1問題
価値が $v_i$ 重さが $w_i$ であるような $N$ 種類の品物と、容量が $W$ のナップザックがあります。
次の条件を満たすように、品物を選んでナップザックに入れます:
・選んだ品物の価値の合計をできるだけ高くする。
・選んだ品物の重さの総和は $W$ を超えない。
・$i$ 番目の品物は $m_i$ 個まで選ぶことができる。←New!!
価値の合計の最大値を求めてください。
入力
1行目に2つの整数 $N$、$W$ が空白区切りで1行に与えられます。 続く $N$ 行で $i$ 番目の品物の価値 $v_i$ と重さ $w_i$ と個数の制限 $m_i$が空白区切りで与えられます。
出力
価値の合計の最大値を1行に出力してください。
制約
$1 ≤ N ≤ 100$
$1 ≤ v_i ≤ 1,000$
$1 ≤ w_i ≤ 1,000$
$1 ≤ m_i ≤ 10,000$ ←New!!
$1 ≤ W ≤ 10,000$
2.1.1.ナップサック問題との違い
・ナップサック問題では、同じ種類の品物を何個でも使ってよかったですが、この問題では文字通り各品物ごとに使っていい個数が決められています。
2.1.2.考え方
・入力例
4 8
4 3 2
2 1 1
1 2 4
3 2 2
・上の入力例を使って、DPテーブルの枠組みを↓のようにしてみます。(いつものDPテーブルに$m_i$が追加されています!!)
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | mi↓ | 0 | |||||||||
| 4 | 3 | 2 | 1 | |||||||||
| 2 | 1 | 1 | 2 | |||||||||
| 1 | 2 | 4 | 3 | |||||||||
| 3 | 2 | 2 | 4 |
・まず考えられるのが、「使っていい品物の個数をバラけさせて、各品物で入れるか入れないか(0-1ナップサック問題)をすれば解決じゃない?」と思いつきます。
・つまり↓のようなDPテーブルです。(各iの品物について入れるか入れないかを考える)
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | mi↓ | 0 | |||||||||
| 4 | 3 | × | 1 | |||||||||
| 4 | 3 | × | 2 | |||||||||
| 2 | 1 | × | 3 | |||||||||
| 1 | 2 | × | 4 | |||||||||
| 1 | 2 | × | 5 | |||||||||
| 1 | 2 | × | 6 | |||||||||
| 1 | 2 | × | 7 | |||||||||
| 3 | 2 | × | 8 | |||||||||
| 3 | 2 | × | 9 |
・しかし、これだと一つの品物の個数が10,000個とかになった時、計算量がやばくなります。(↓みたいな、全部の品物の個数が10,000個だったらさらにヤバイ、、、)
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | mi↓ | 0 | |||||||||
| 4 | 3 | 10000 | 1 | |||||||||
| 2 | 1 | 10000 | 2 | |||||||||
| 1 | 2 | 10000 | 3 | |||||||||
| 3 | 2 | 10000 | 4 |
↓ じゃあどうするか
一個ずつに分けるのではなく、「繰り返し二乗法」(厳密には違う)という手法で$m_i$を分解し、計算量を減らします!!!!!
2.2.繰り返し二乗法の「分解」
・繰り返し二乗法に使われている「分解」を使うので、厳密には繰り返し二乗法ではないというわけですね!
2.2.1.この分解で何が嬉しいの?
一個一個分解して計算するより、計算量が減る!!!
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | mi↓ | 0 | |||||||||
| 4 | 3 | 2 | 1 | |||||||||
| 2 | 1 | 1 | 2 | |||||||||
| 1 | 2 | 4 | 3 | |||||||||
| 3 | 2 | 2 | 4 |
・例えば上の表の$i=3$の品物を考えます。
\begin{align}
m_i &= 4 \\
&= 2^0+2^1+1\\
&= 1+2+1\\
\end{align}
に分けることができます。
・つまり品物を[価値=1、重さ=2]、[価値=2、重さ=4]、[価値=1、重さ=2]に分解して、各品物ごとに、入れるか入れないか(0-1ナップ)をします。
・$m_i=10000$とかになると、さらに計算量を減らすことができます。
・全ての品物を分解したら、あとは0-1ナップサック問題と同じ、入れるか入れないかを考えていきます。
2.3.DPテーブルを作る
・DPテーブルの埋め方は0-1ナップサック問題と同じ考え方です。
i:品物の番号
j:容量の大きさ
として
$$\boldsymbol{dp[i][j]=i番目までの品物を使って、容量がjを超えないようなvの最大値}$$
↓
dp[i][j] = \left\{
\begin{array}{ll}
dp[i-1][j] & (j<w) \\
max(dp[i-1][j], dp[i-1 ][j-w]+v) & (otherwise)
\end{array}
\right.
としてdp表を埋めていきます。
2.4.実装
# 入力値取得
N,W=map(int,input().split())
# mi(品物の個数)を分解した後の、v(価値)とw(重さ)を入れるリストを作る
L=[]
for _ in range(N):
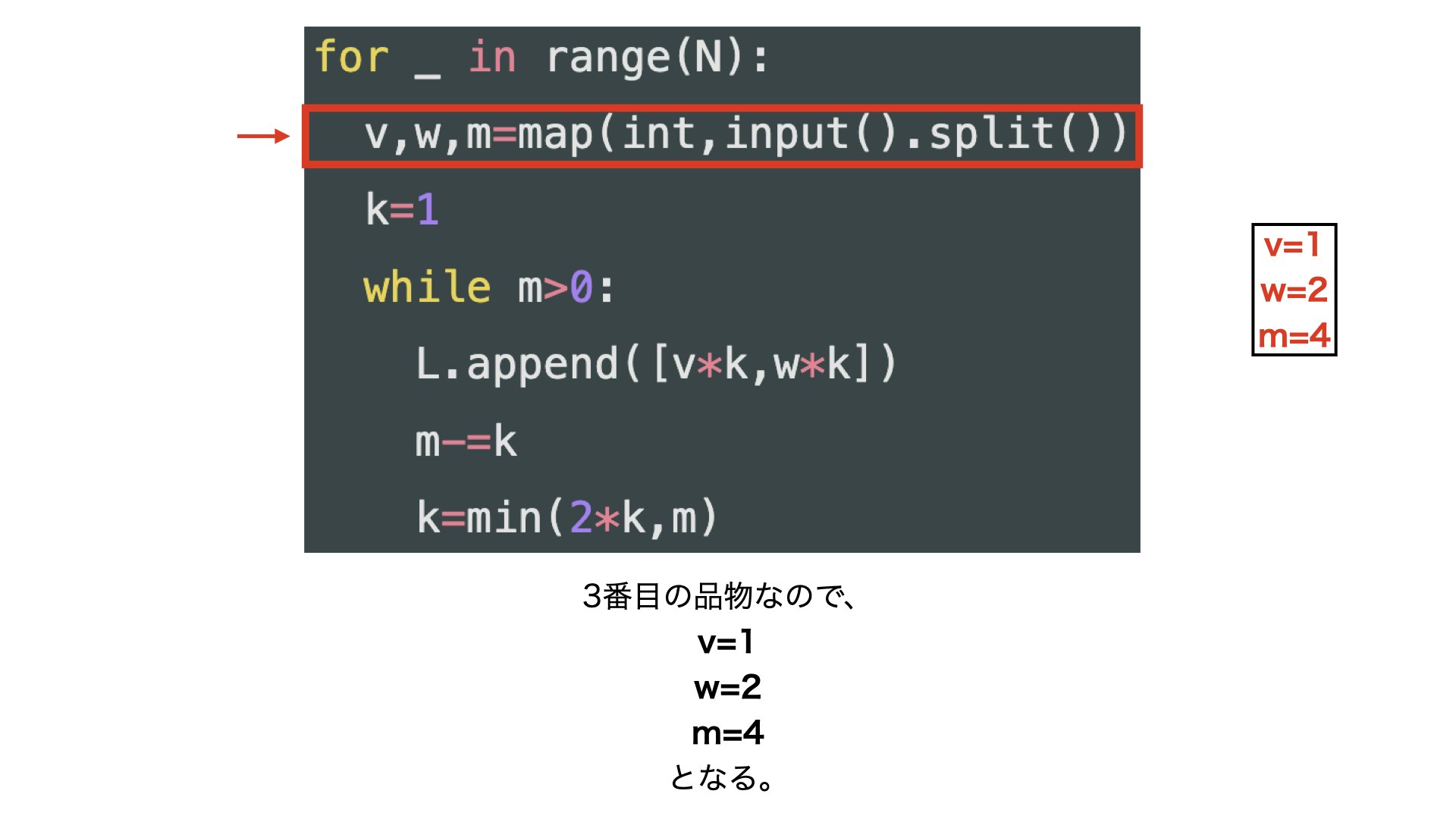
v,w,m=map(int,input().split())
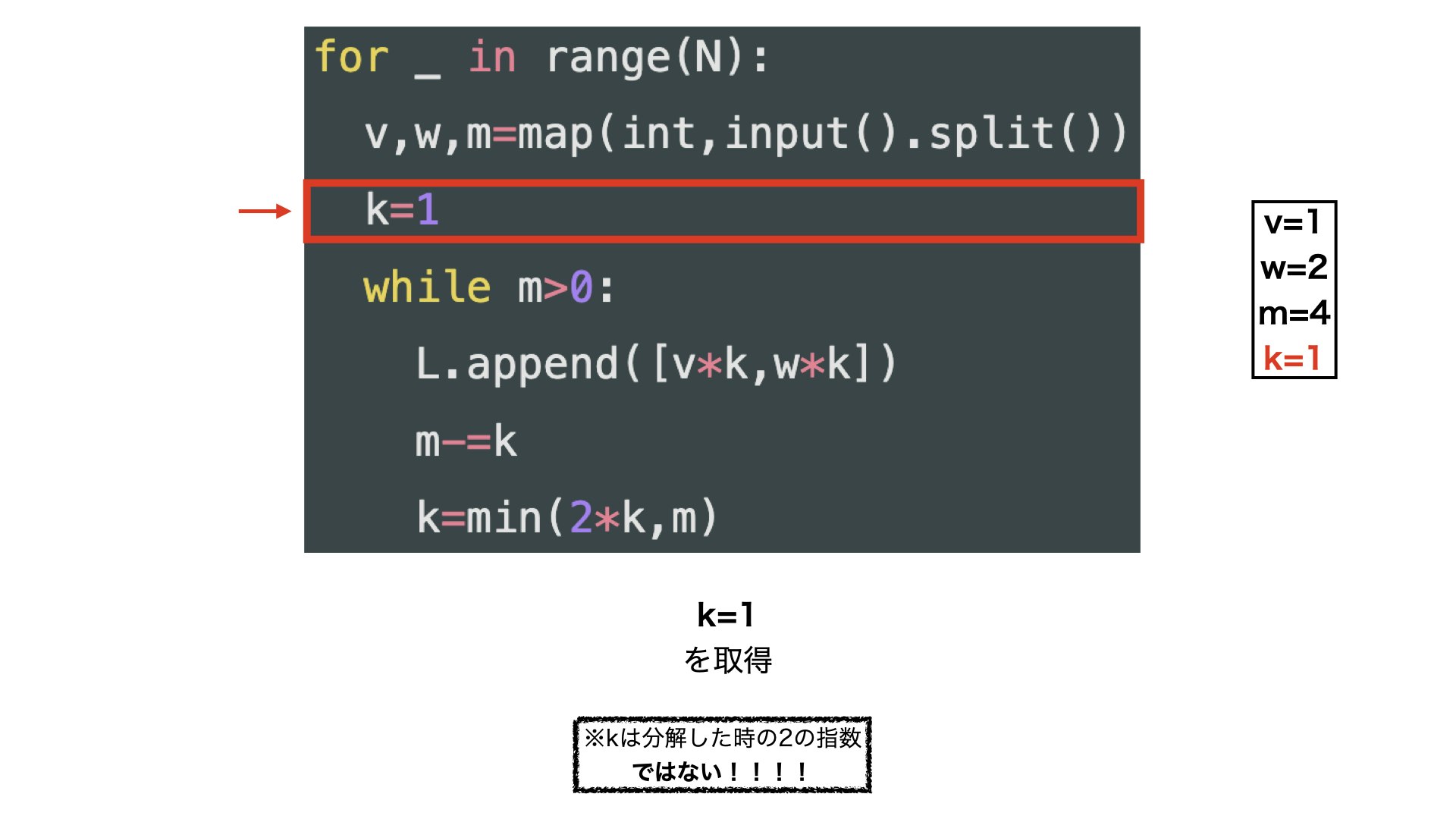
k=1
while m>0:
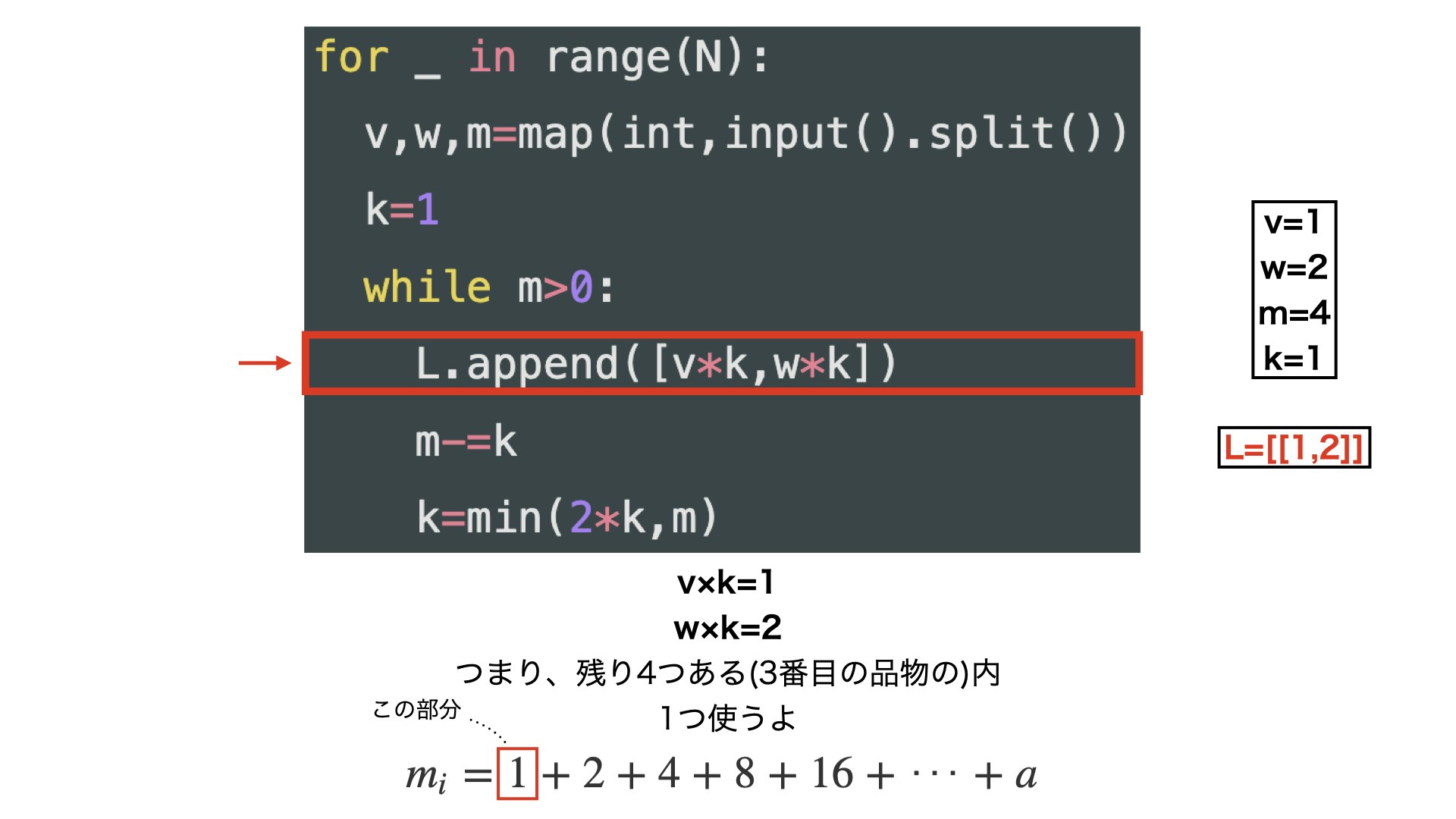
L.append([v*k,w*k])
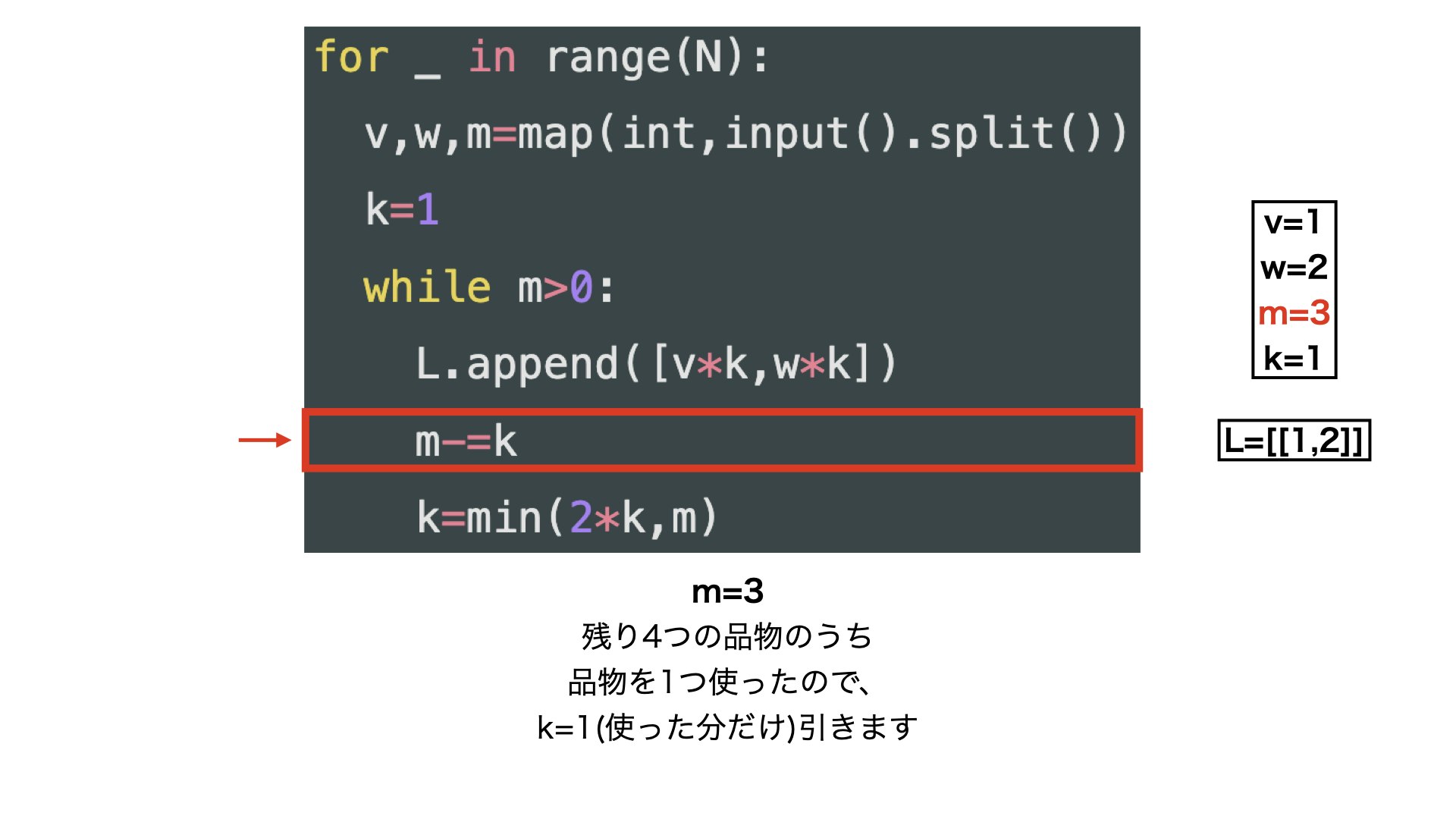
m-=k
k=min(2*k,m)
# DP表作成(一次元)
dp=[0]*(W+1)
# 分解した品物が入ってるリストからv,wをとって回す
# 0-1ナップの一次元と同じ回し方(WとWeの違いに注意!)
for v,w in L:
for j in range(W,w-1,-1):
dp[j]=max(dp[j],dp[j-w]+v)
print(dp[W])
2.4.1.分解するときのコードについて
for _ in range(N):
v,w,m=map(int,input().split())
k=1
while m>0:
L.append([v*k,w*k])
m-=k
k=min(2*k,m)
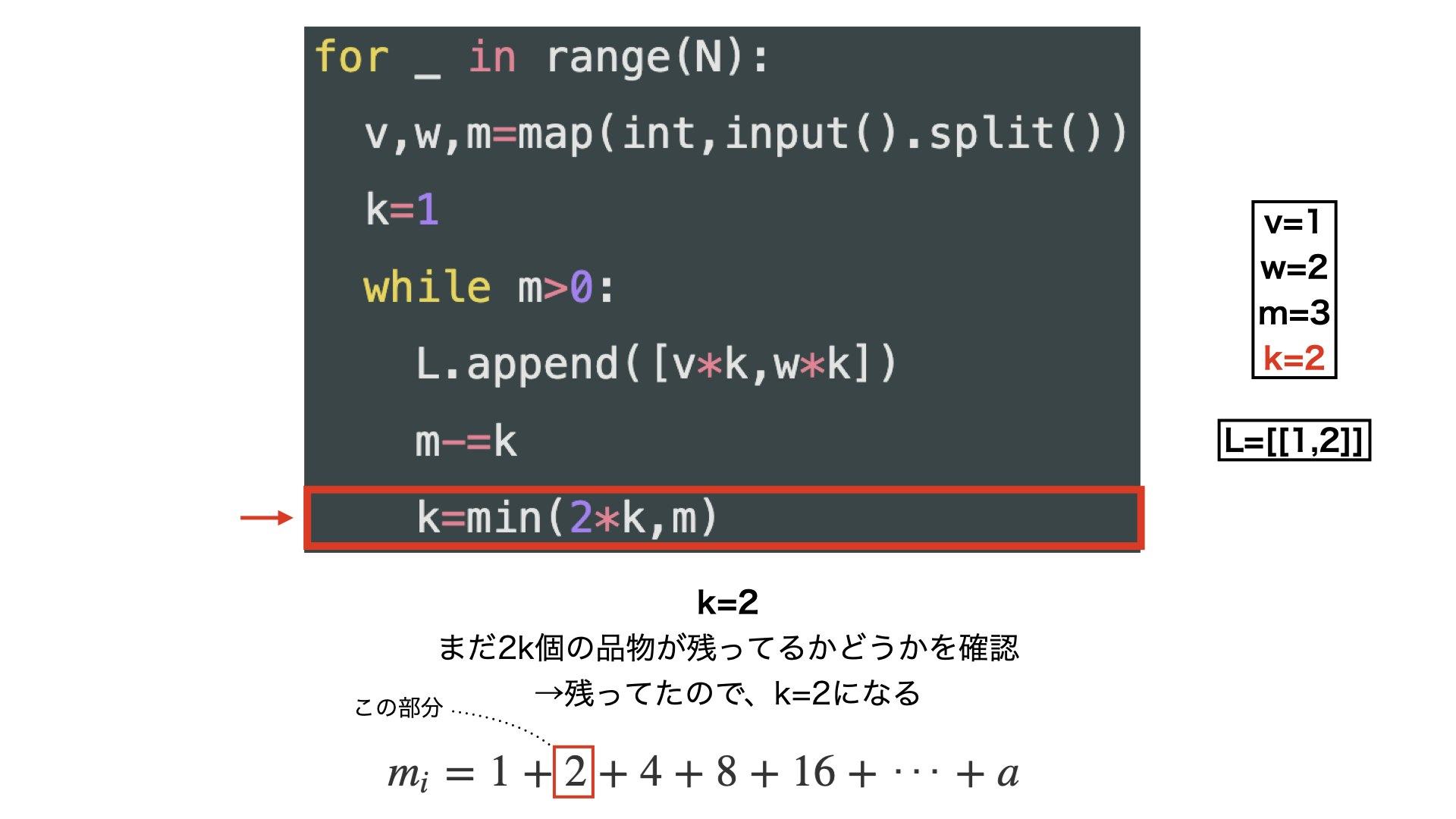
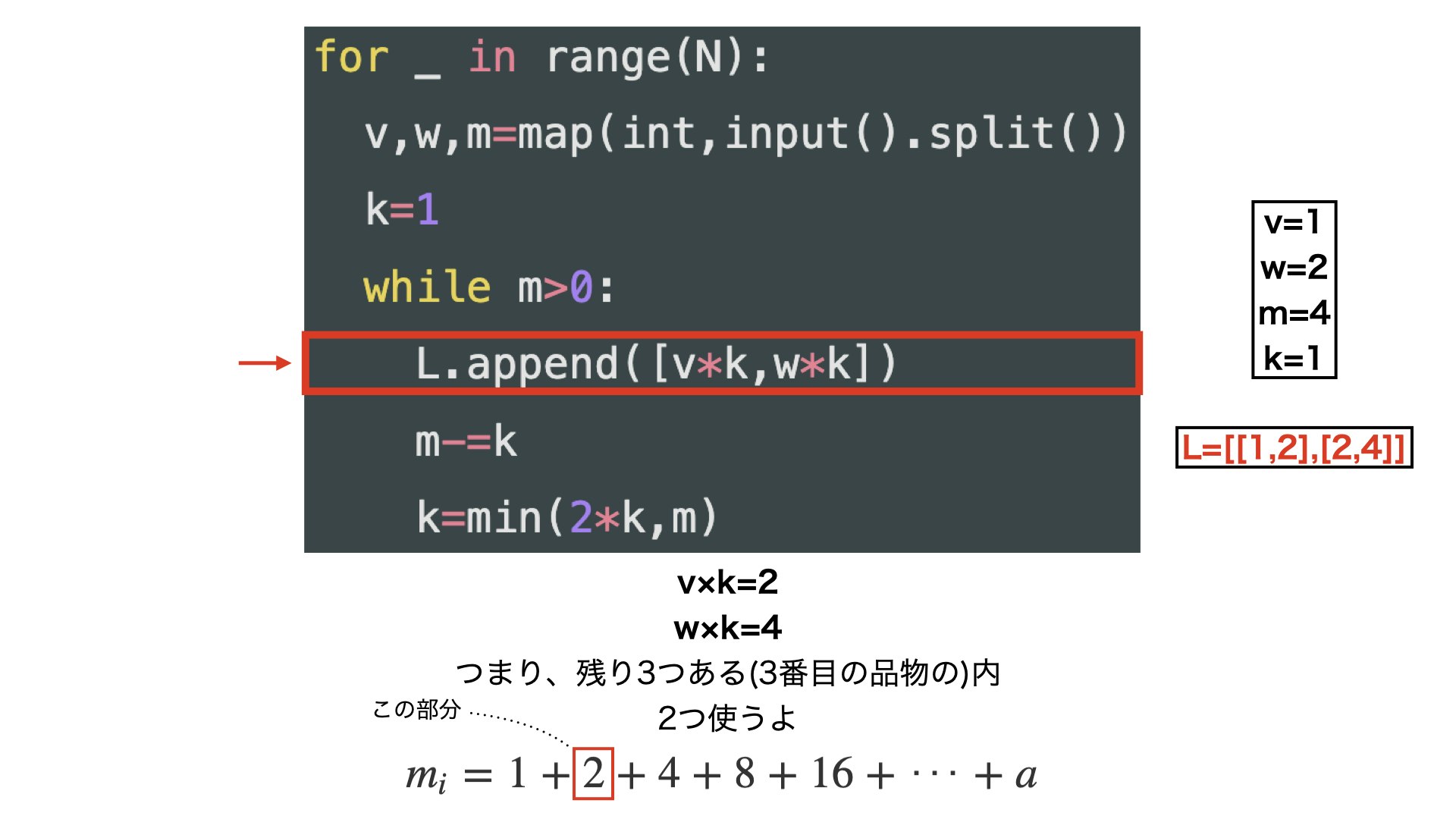
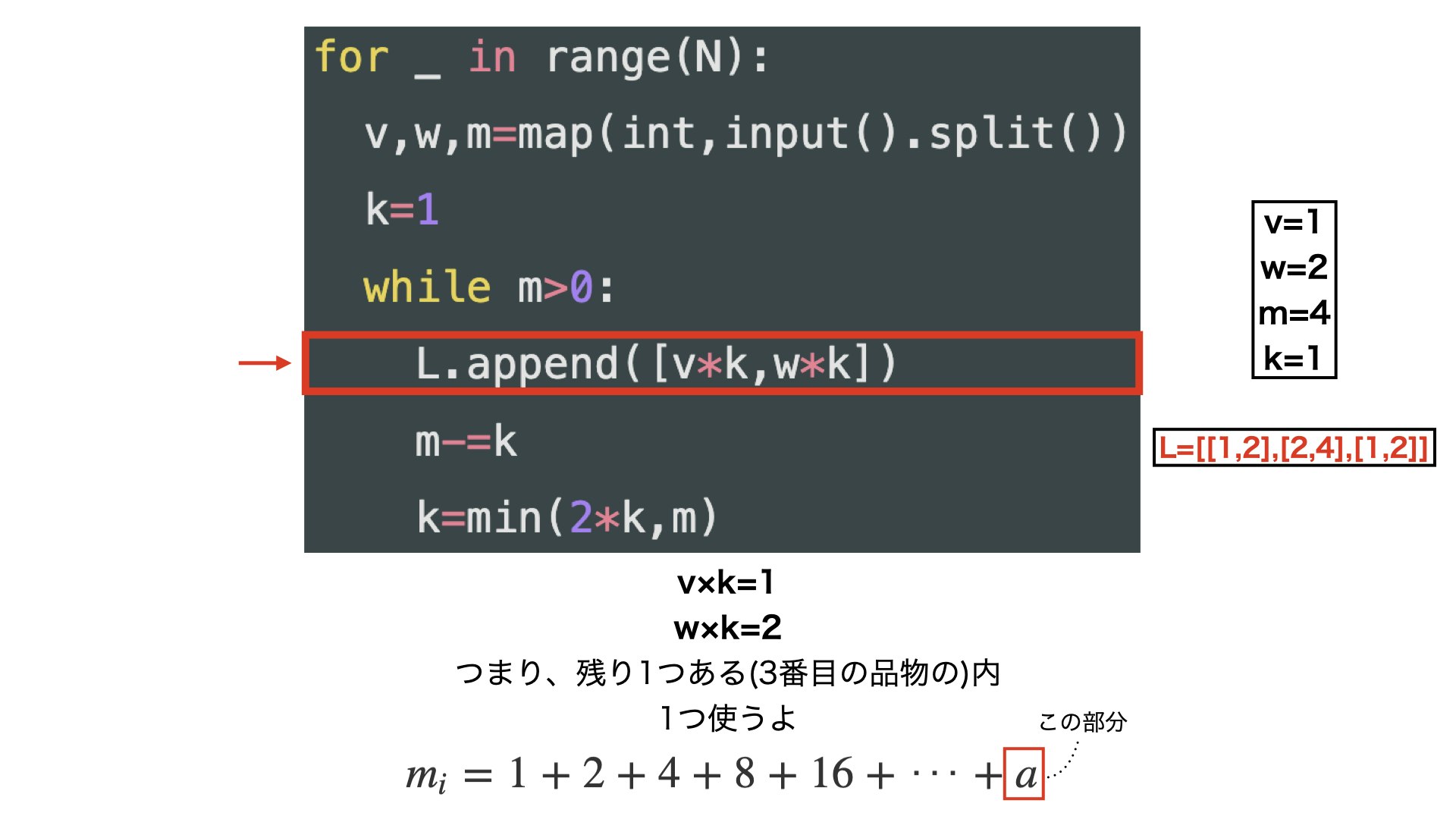
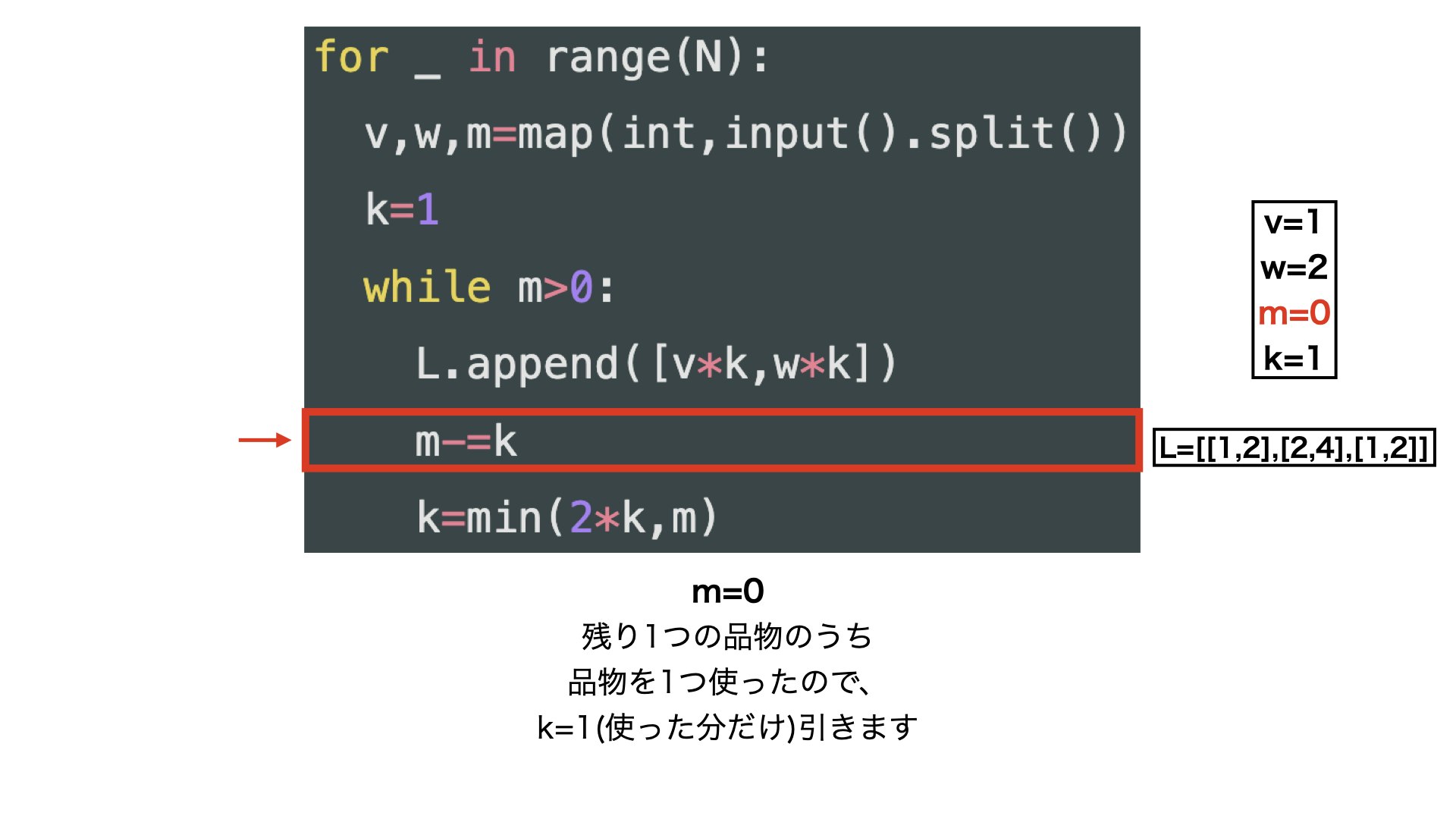
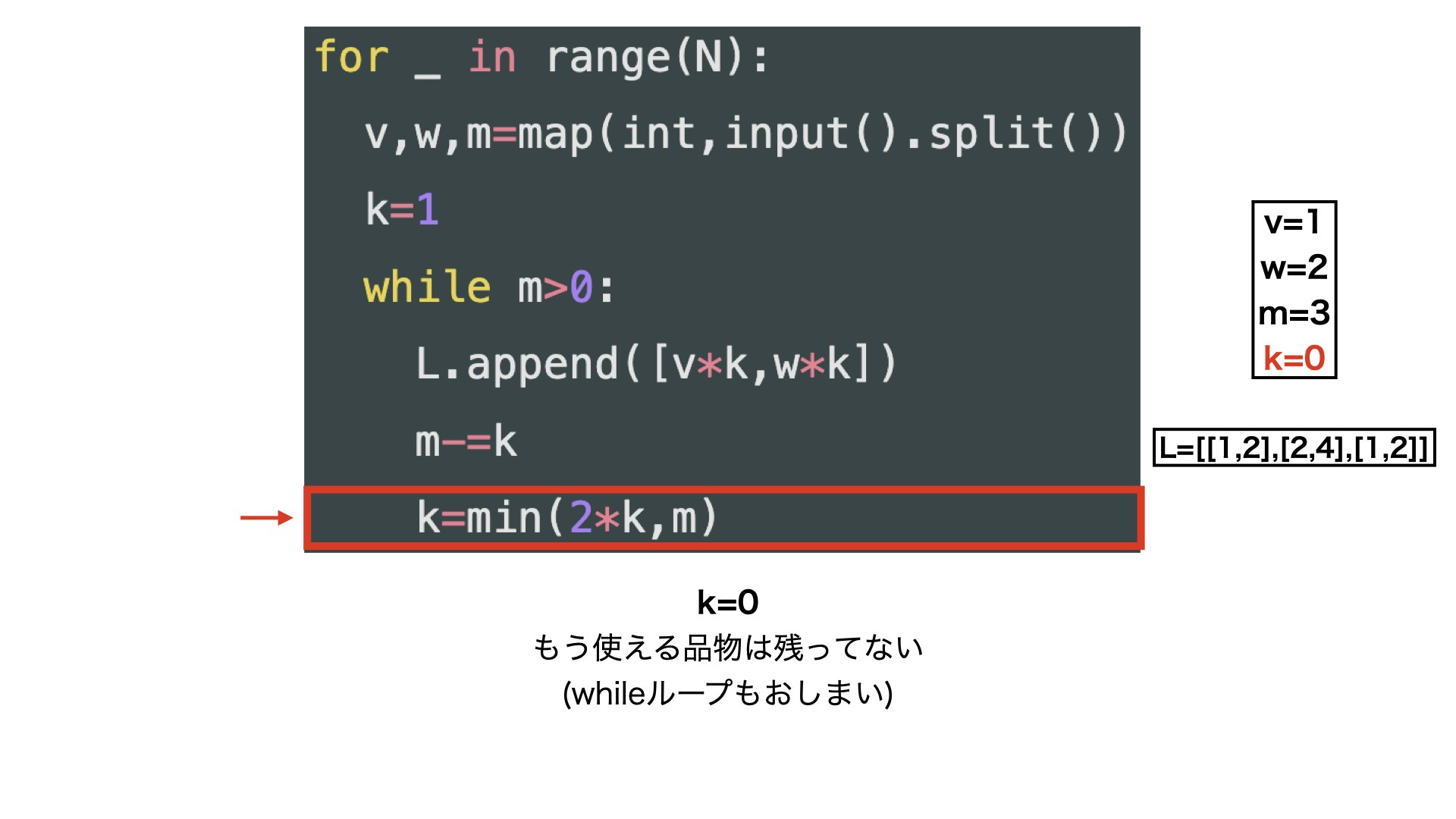
・分解する時の↑のコードの流れを少しだけ詳しくみていきたいと思います。
| i\j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| vi↓ | wi↓ | mi↓ | 0 | |||||||||
| 4 | 3 | 2 | 1 | |||||||||
| 2 | 1 | 1 | 2 | |||||||||
| 1 | 2 | 4 | 3 | |||||||||
| 3 | 2 | 2 | 4 |
・上の表のi=3(3番目の品物)の時を例に考えます。
・みたいな感じです。