【ラビットチャレンジ（E資格）】深層学習day2

はじめに

本記事はJDLA E資格の認定プログラム「ラビット・チャレンジ」における深層学習day2のレポート記事です。
本記事では以下の5つの項目について、要点をまとめています。

• 勾配消失問題
• 学習率最適化手法
• 過学習
• 畳み込みニューラルネットワークの概念
• 最新のCNN

1. 勾配消失問題

概要

誤差逆伝播法が下位層に進んでいくにつれて勾配はどんどん緩やかになっていきます。そのため、勾配降下法による更新では、下位層のパラメータがほとんど変わらず、訓練が最適値に収束しなくなります。

勾配消失の解決方法は大きく3つの方法があります。

• 活性化関数の選択
  ReLU関数を使用することで、勾配消失問題の回避とスパース化に貢献することができます。
  ReLU関数は入力値が閾値(0)を超えている場合、入力値をそのまま出力する関数です。今最も使われている活性化関数です。

• 重みの初期値設定
  重みの初期値設定はとても重要です。大きく2つの設定方法があります。

  • Xavier
    重みの要素を、前の層のノード数（ユニット数）の平方根で除算した値を初期値とするアルゴリズム。
    Xavier初期値を設定する際の活性化関数は、ReLU関数、シグモイド関数、双曲線正接関数(tanh)があげられます。
  • He
    重みの要素を、前の層のノード数(ユニット数)の平方根で除算した値に$\sqrt{2}$を掛けた値を初期値とするアルゴリズム。
    Heの初期値を設定する際の活性化関数は、ReLU関数があげられます。

• バッチ正規化
  ミニバッチ単位で入力値のデータの偏りを抑制する手法です。
  活性化関数に値を渡す前後にバッチ正規化の処理を含む層を加えます。

コード実装

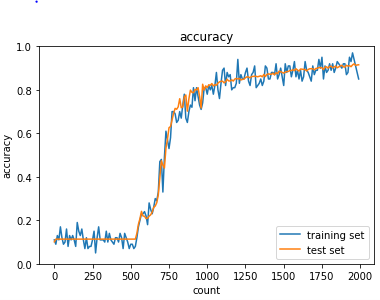
MNISTの手書き文字データセットを使用して勾配消失問題について検討しました。
以下のコードでは、活性化関数にシグモイド関数、初期値はガウス関数を元に生成した乱数としています。

sigmoid-gauss

import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt

# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)

print("データ読み込み完了")

# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20

#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10

# 初期設定
def init_network():
    network = {} 
    network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
    network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
    network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)

    network['b1'] = np.zeros(hidden_layer_1_size)
    network['b2'] = np.zeros(hidden_layer_2_size)
    network['b3'] = np.zeros(output_layer_size)

    return network

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_f = functions.sigmoid
    
    u1 =  np.dot(x, W1) + b1
    z1 = hidden_f(u1)
    u2 =  np.dot(z1, W2) + b2
    z2 = hidden_f(u2)
    u3 =  np.dot(z2, W3) + b3
    y = functions.softmax(u3)
 
    return z1, z2, y

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    hidden_d_f = functions.d_sigmoid
    last_d_f = functions.d_softmax_with_loss
    
    
    # 出力層でのデルタ
    delta3 = last_d_f(d, y)
    # b3の勾配
    grad['b3'] = np.sum(delta3, axis=0)
    # W3の勾配
    grad['W3'] = np.dot(z2.T, delta3)
    # 2層でのデルタ
    delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 1層でのデルタ
    delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# パラメータの初期化
network = init_network()

accuracies_train = []
accuracies_test = []

# 正答率
def accuracy(x, d):
    z1, z2, y = forward(network, x)
    y = np.argmax(y, axis=1)
    if d.ndim != 1 : d = np.argmax(d, axis=1)
    accuracy = np.sum(y == d) / float(x.shape[0])
    return accuracy

for i in range(iters_num):
    # ランダムにバッチを取得    
    batch_mask = np.random.choice(train_size, batch_size)
    # ミニバッチに対応する教師訓練画像データを取得    
    x_batch = x_train[batch_mask]
    # ミニバッチに対応する訓練正解ラベルデータを取得する
    d_batch = d_train[batch_mask]


    
    z1, z2, y = forward(network, x_batch)
    grad = backward(x_batch, d_batch, z1, z2, y)

    if (i+1)%plot_interval==0:
        accr_test = accuracy(x_test, d_test)
        accuracies_test.append(accr_test)
        
        accr_train = accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)

        print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))

    # パラメータに勾配適用
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network[key]  -= learning_rate * grad[key]


lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()

【出力結果】

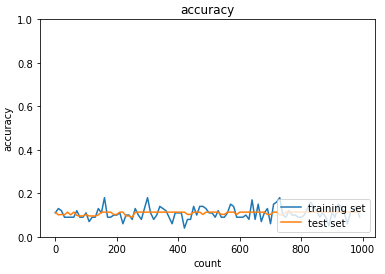
Generation: 2000. 正答率(トレーニング) = 0.10
　　　　　: 2000. 正答率(テスト) = 0.11

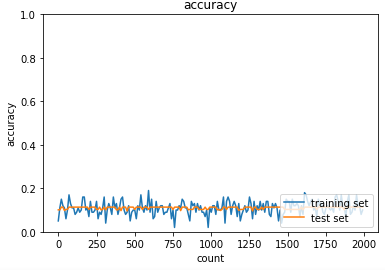
どれだけ学習をしても正解率が一向に上がらないことが分かる。
これは、勾配が消失して学習が進んでいないことが原因である。

続いて、初期値はそのままに、活性化関数をReLUに変えてみる。

ReLU-gauss

# 変更箇所のみ記載
# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    ###########  変更箇所  ###########
    hidden_f = functions.relu
    #################################

# 誤差逆伝播
def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    ###########  変更箇所  ###########
    hidden_d_f = functions.d_relu
    #################################

【出力結果】

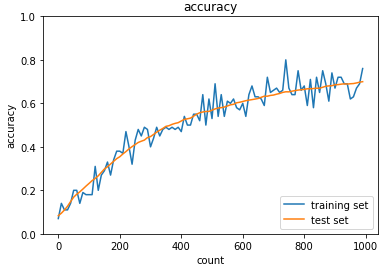
Generation: 2000. 正答率(トレーニング) = 0.85
　　　　　: 2000. 正答率(テスト) = 0.92

学習するにつれて正解率が上がっていることが分かる。
活性化関数をReLUに変更したことで勾配消失問題を解決できた。このように、勾配消失と活性化関数は密接に関わっていることが分かる。

さらに、初期値をHe、活性化関数をReLUとして学習をさせた。

ReLU-He

# 変更箇所のみ記載
# 初期設定
def init_network():
    network = {} 

    ###########  変更箇所  ##############
    # Heの初期値
    network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / np.sqrt(input_layer_size) * np.sqrt(2)
    network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / np.sqrt(hidden_layer_1_size) * np.sqrt(2)
    network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / np.sqrt(hidden_layer_2_size) * np.sqrt(2)    
    #################################

# 順伝播
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    ###########  変更箇所  ##############    
    hidden_f = functions.relu    
    #################################

def backward(x, d, z1, z2, y):
    grad = {}
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    ###########  変更箇所  ##############    
    hidden_d_f = functions.d_relu    
    #################################

【出力結果】

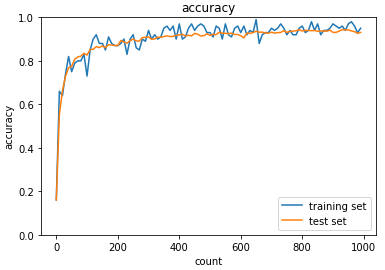
Generation: 2000. 正答率(トレーニング) = 0.96
　　　　　: 2000. 正答率(テスト) = 0.96

学習の早い段階で正解率が80%を超え、最終的な正解率も96%と高い。先ほどのgaus-ReLUの結果と比べても、学習のスピード、正解率ともに良くなっていることが分かる。このように、重みの初期値の設定も学習と密接に関わっていることが分かる。

確認テスト

###確認テスト1
連鎖律の原理を使い、$z=t^2$、$t=x+y$の時の$dz/dx$を求めよ。

解答：

\frac{dz}{dx}=\frac{dz}{dt}\frac{dt}{dx}=2t\times1=2(x+y)

###確認テスト2
シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値を答えよ。

解答：
シグモイド関数の微分の式は以下となる。

f(u)=(1-sigmoid(u))\cdot sigmoid(u)

シグモイド関数の入力が0の時、出力は0.5となるため、代入すると$0.5\times0.5=0.25$となる。

###確認テスト3
重みの初期値に0を設定すると、どのような問題が発生するか。

解答：
全てのパラメータが同じ値で伝搬していくためチューニング（値の最適化）がされなくなるため学習が進まなくなる。

###確認テスト4
一般的に考えられるバッチ正規化の効果を2点挙げよ。

解答：
・勾配消失問題の抑制
・計算の効率化

2. 学習率最適化手法

概要

初期の学習率の設定方法の指針は以下の2つです。
・初期の学習率を大きく設定し、徐々に学習率を小さくする。
・パラメータごとに学習率を可変させる。

学習率の最適化は、学習率最適化手法を利用します。各手法について説明していきます。

• モメンタム
  勾配降下法では、誤差をパラメータで微分したものと学習率の積を減算していました。
  モメンタムでは、誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算する。

V_{t}=\mu V_{t-1}-\epsilon\nabla E

w^{t+1}=w^{t}+V_{t}

メリットとしては、局所的最適解にはならず、大域的最適解となる。また、谷間から最適解までたどり着くのが早い。

• AdaGrad
  誤差をパラメータで微分したものと再定義$\epsilon\frac{1}{\sqrt{h_{t}}+\theta}\nabla E$した学習率の積を減算する。

h_{0}=\theta

h_{t}=h_{t-1}+(\nabla E)^2

w^{t+1}=w^{t}-\epsilon\frac{1}{\sqrt{h_{t}}+\theta}\nabla E

勾配の緩やかな斜面に対して最適解に近づけることができる。
課題として、学習率が徐々に小さくなるので鞍点問題を引き起こすことがある。

• RMSProp
  AdaGradの問題を改良したもの。

h_{t}=\alpha h_{t-1}+(1-\alpha)(\nabla E)^2

w^{t+1}=w^{t}-\epsilon\frac{1}{\sqrt{h_{t}}+\theta}\nabla E

AdaGradと比較して局所最適解にならず大域的最適解になる、ハイパーパラメータの調整が必要な場合が少ない。

• Adam
  モメンタムとRMSPropのメリットを含んだアルゴリズムで、効率的にパラメータ空間を探索すること期待できる。
  また、ハイパーパラメータの「バイアス補正（偏りの補正）」が行われていることもAdamの特徴である。

これらの手法について以下のリンクがとても参考になりました。
最適化手法について、視覚的に理解を深めることができます。
https://github.com/Jaewan-Yun/optimizer-visualization

コード実装

上記の数式を実装していきます。

モメンタム

class Momentum:
    def __init__(self, learning_rate=0.01, momentum=0.9):
        self.learning_rate = learning_rate
        self.momentum = momentum
        self.v = None
        
    def update(self, params, grad):
        if self.v is None:
            self.v = {}
            for key, val in params.items():                                
                self.v[key] = np.zeros_like(val)
                
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.learning_rate * grad[key] 
            params[key] += self.v[key]

AdaGrad

class AdaGrad:
    def __init__(self, learning_rate=0.01):
        self.learning_rate = learning_rate
        self.h = None
        
    def update(self, params, grad):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] += grad[key] * grad[key]
            params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)

RMSprop

class RMSprop:
    def __init__(self, learning_rate=0.01, decay_rate = 0.99):
        self.learning_rate = learning_rate
        self.decay_rate = decay_rate
        self.h = None
        
    def update(self, params, grad):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
            
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grad[key] * grad[key]
            params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)

Adam

class Adam:
    def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999):
        self.learning_rate = learning_rate
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grad):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.learning_rate * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)         
        
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grad[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grad[key] ** 2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

以下は、最適化手法について色々検討してみた結果です。
データセットはMNISTを使用しています。

• 学習率を変化させてみる
  最適化手法：モメンタム
  活性化関数：sigmoid
  初期値：gauss

【学習率：0.01】

【学習率：0.9】

学習率0.01の時は学習が進まなかったが、0.9にすることで学習が進み正解率が高くなった。
このことから、学習最適化には適切な学習率の設定が必要であることが分かる。

• 活性化関数を変化させてみる
  最適化手法：Adam
  学習率：0.01
  初期値：gauss

【活性化関数：sigmoid】

【活性化関数：ReLU】

ReLU関数の方が学習が早く進んでいる。
このことから、学習最適化には適切な活性化関数の選択が必要であることが分かる。

• バッチ正規化を行う
  上記の活性化関数をReLUとした条件において、バッチ正規化を行う。
  バッチ正規化は、学習のミニバッチ毎に各チャンネルを平均0、分散1になるように正規化することで、学習の安定化や速度がアップする手法である。
  

バッチ正規化を行うことで、学習がより早く進んでいることがわかる。また、正解率についても改善がみられている。

確認テスト

モメンタム、AdaGrad、RMSpropの特徴をそれぞれ簡潔に説明せよ。

解答：

• モメンタム：勾配の移動平均を出して振動を抑える（過去の勾配たちを考慮することで急な変化を抑える）。
• AdaGrad：次元ごとに学習率を変化させるようにしたもの。
• RMSprop：AdaGradの改良版であり、一度学習率が0に近づくとほとんど変化しなくなるAdaGradの問題を改良したもの。

3. 過学習

概要

過学習とは、テスト誤差と訓練誤差で学習曲線が乖離することです。
つまり、特定のサンプルに対して特化して学習をしてしまっている状態になります。
原因としては、パラメータの数が多い、パラメータの値が適切でない、ノードの数が多い等があげられます。
それでは、この過学習についての対策方法についてご紹介していきます。

• L1, L2正則化
  $p=1$ならL1正則化、$p=2$ならL2正則化。
  $\lambda$は減衰させるスケーリングのための値になります。

E_{n}(w)+\frac{1}{p}\lambda ||x||_{p}

||x||_{p}=(|x_{1}|^{p}+...+|x_{n}|^{p})^{\frac{1}{p}}

• ドロップアウト
  ノードが多いというのが過学習の原因の一つでした。
  ドロップアウトはランダムにノードを削除して学習させることでこの課題を解決させます。
  この手法は、データ量を変化させずに、異なるモデルを学習させていると解釈できます。

コード実装

過学習の抑制について検討するため、正則化やドロップアウトについて実装をしました。
MNISTのデータセットを使用しています。

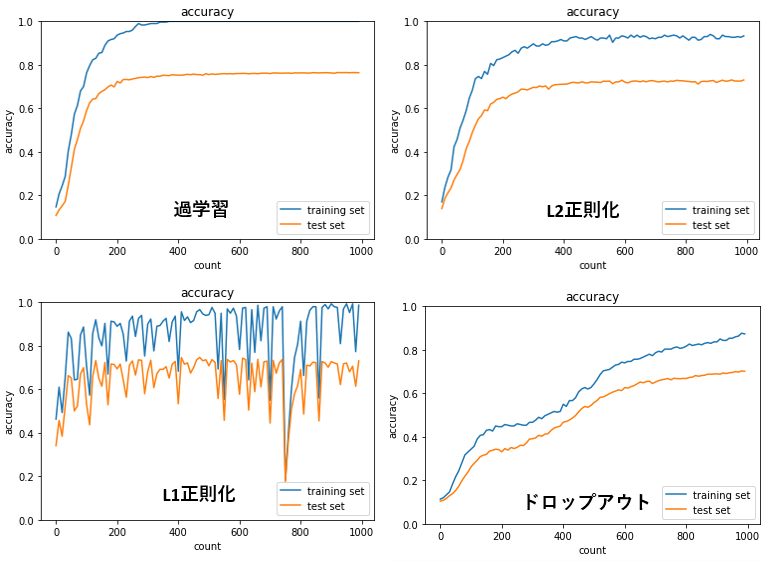
L2正則化、L1正則化、ドロップアウトを導入することにより、過学習が抑制できていることが分かります。
L2正則化は安定して学習が進む一方で、L1正則化での学習は不安定になっています。
ドロップアウトは、学習の進みが遅いということが分かります。

• 正則化の強さを変更してみる（L2正則化）

【正則化強度：0.1】

【正則化強度：0.2】

結果を比較すると、正則化強度が0.2の方が、trainingとtestが近く過学習が抑制できています。一方で、正解率は低くなってしまっています。
このことから、正則化強度が強いほど過学習を抑制させることができるが、正解率を下げてしまうことが分かります。正則化強度は学習に大きな影響を与えており、適切に設定する必要があります。

• ドロップアウトの閾値を変更してみる

【ドロップアウト閾値：0.15】

【ドロップアウト閾値：0.1】

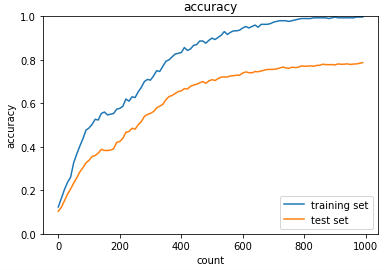
ドロップアウト閾値を下げることにより学習は進んだが、過学習は大きくなってしまいました。
こちらも適切に設定する必要があることが分かります。

• ドロップアウト＋L1正則化
  【ドロップアウト閾値：0.08】
  【正則化強度：0.004】
  

【ドロップアウト閾値：0.15】
【正則化強度：0.004】

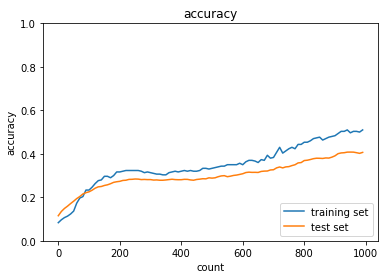
L1正則化とドロップアウトを組み合わせることで、L1正則化単体での学習の不安定さは解消されています。
過学習を抑える手法を組み合わせることで精度の改善は期待できそうです。
一方で、ハイパーパラメータが増えことにより調整が難しくなっています。
グリッドサーチやランダムサーチなどの、ハイパーパラメータ探索が必要と感じました。
いずれにせよ、ドロップアウトも正則化も過学習を抑制させる方法として重要な手法であることがわかります。

確認テスト

下図について、L1正則化を表しているグラフはどちらか答えよ。

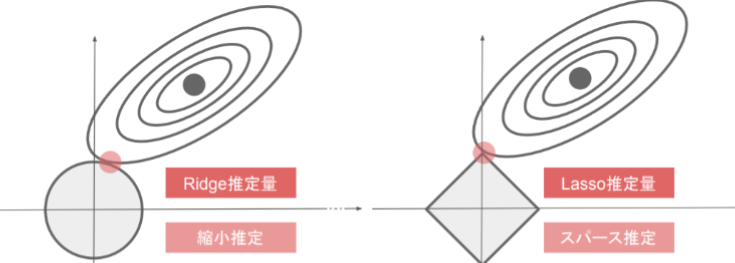
（図はラビット・チャレンジの講義資料から引用）

解答：
右のLasso推定量がL1正則化を表している。Lasso推定量ではスパース推定がされている。

4. 畳み込みニューラルネットワークの概念

概要

畳み込みニューラルネットワーク（convolutional neural network：CNN）は、画像認識や音声認識など、至るところで使われています。CNNは畳み込み層・プーリング層・全結合層で構成される順伝播型ニューラルネットワークです。
これまで扱ってきたニューラルネットワークは、隣接する層の全てのニューロン間で結合がありました。これを全結合層と呼びます（図中ではAffineとしています）。

これに対してCNNでは新しく、畳み込み層(conv)とプーリング層(Pooling)が加わりました。レイヤーのつながりは順は「conv - ReLU - (Pooling)」という流れになっています。
CNNでも、出力層に近い層では、これまでの「Affine - ReLU」という組み合わせが用いられます。また、最後の層においては、「Affine - Softmax」の組み合わせが用いられます。これらは一般的なCNNでもよく見られる構成です。

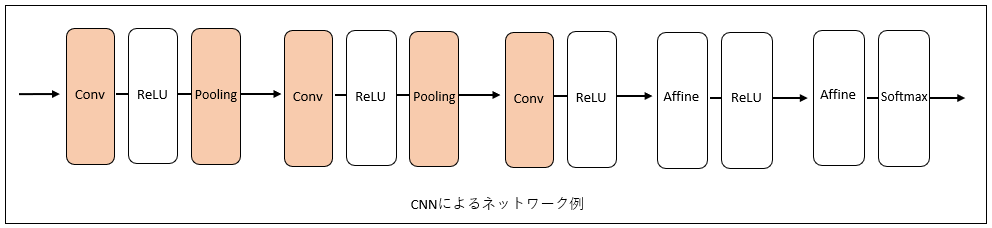
それでは各層について詳しく見ていきます。

畳み込み層

畳み込み演算

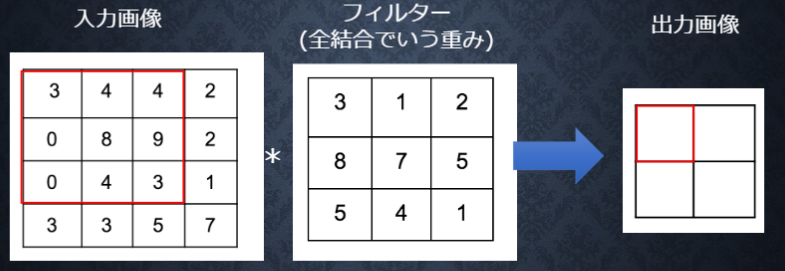
畳み込み演算は、画像処理でいうところの「フィルタ―演算」に相当します。

（図はラビット・チャレンジ講義資料から引用）

畳み込み演算は、入力データに対してフィルター（カーネル）を適用します。入力データに対して、フィルターのウィンドウを一定の間隔でスライドさせながら適用していきます。それぞれの場所でフィルターの要素と入力の対応する要素を乗算し、その和を求めます。そして、その結果を出力の対応する場所へ格納していきます。
例えば、図の赤枠で囲まれている出力画像の値を求めるとしたら、フィルターを入力画像の赤枠に適用します。計算は以下のように行います。
$$3\times3+4\times1+4\times2+0\times8+8\times7+9\times5+0\times5+4\times4+3\times1=141$$
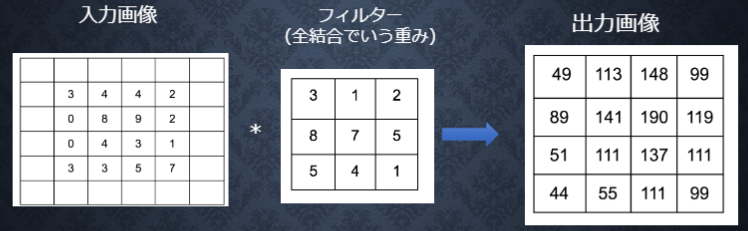
この演算をフィルターを一つ一つずらしながらすべての入力画像に対して行います。
以下は、バイアスも含めた畳み込み演算になります。

（図はラビット・チャレンジ講義資料から引用）

バイアス項の加算は、フィルタ適用後のデータに対して行われます。フィルター適用後のデータに対してバイアスは一つとなります。

パディング

畳み込み層の処理を行う前に、入力データの周囲に固定のデータ（例えば0）を埋めることがあります。これをパディングと言い、畳み込み演算でよく用いられる処理になります。
パディングを行う理由は出力サイズを調整するためです。畳み込み演算を何度も繰り返すと、データが圧縮されてしまい、ある時点で出力サイズが1になってしまい、それ以上畳み込み演算を適用できなくなってしまいます。

（図はラビット・チャレンジ講義資料から引用）

ストライド

フィルターを適用する位置の間隔をストライドといいます。これまで見てきた例ではストライドは1でした。
例えば、ストライドを2のようにすると下図のようになります。

（図はラビット・チャレンジ講義資料から引用）

ストライドを大きくすると、出力はサイズは小さくなります。一方で、パディングを大きくすると出力サイズは大きくなります。このような関係を定式化します。
入力サイズを$W\times H$、フィルタサイズを$Fw\times Fh$、パディングを$p$、ストライドを$s$とし、畳み込み層の出力サイズを$OW\times OH$とすると、$OW$および$OH$は次の式により求められます。
$$OW=\frac{W+2p−Fw}{s}+1$$
$$OH=\frac{H+2p−Fh}{s}+1$$

チャンネル

これまで見てきた例では、入力データは$W\times H$の2次元画像でしたが、3次元となっても畳み込み演算は可能です。チャンネルを増やす例としては、RGBのカラー画像を学習するときが考えられます。R、G、Bのそれぞれを各チャンネルとしCNNへの入力として扱います。

プーリング層

プーリング層は、縦・横方向の空間を小さくする演算です。例えば下図のように、$3×3$の領域を一つの要素に集約するような処理を行い、空間サイズを小さくします。

（図はラビット・チャレンジ講義資料から引用）

Maxプーリングは$3×3$の領域に対して最大となる要素を取り出します。この例でいうと、出力の赤枠には9が要素となります。Maxプーリングの他に、対象領域の平均を要素として取り出すAverageプーリングなどもあります。
プーリングは、入力データの小さなずれに対して、同じような結果を返します。そのため、入力データの微小なずれに対してロバストになります。

確認テスト

サイズ$6\times6$の入力画像を、サイズ$2\times2$のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なお、ストライドとパディングは1とする。

解答：

求める出力幅を$OW$、出力高を $OH$とすると、以下のように求められます。
$$OW=\frac{W+2p−Fw}{s}+1=\frac{6+2−2}{1}+1=7$$
$$OH=\frac{H+2p−Fh}{s}+1=\frac{6+2−2}{1}+1=7$$

5. 最新のCNN

概要

2021年現在では最新の手法ではないですが、AlexNetについて概要をまとめます。

AlexNetは2012年の画像認識コンペILSVRCにおいて圧倒的な精度を誇ったモデルです。
この論文で提案されたモデルは、5層の畳み込み層と3つの全結合層を持つCNNで筆頭著者のAlexさんの名前を取ってAlexNetと呼ばれています。

図は論文 (ImageNet Classification with Deep Convolutional Neural Networks) から引用
URL (https://www.cs.toronto.edu/~kriz/imagenet_classification_with_deep_convolutional.pdf)

モデルの構造は以下のようになっています。

• 第1層: 224×224×3の画像を11×11×3の96個のkernelに変換
• 第2層: LRN & poolingした結果を5×5×48の256個のkernelに変換
• 第3層: LRN & poolingした結果を3×3×256の384個のkernelに変換
• 第4層: 3×3×192の384個のkernelに変換
• 第5層: 3×3×192の256個のkernelに変換
• 2つの全結合層: 4096個のニューロン
• 出力層: 1000個のsoft-maxニューロン

活性化関数としてReLUを用いたこと、マルチGPUでの学習、LPNを正規化として使用、Overlapping Poolingによる過学習抑制などが精度に寄与したとのことです。

最新論文・手法の情報収集

最新論文や最新の手法について調査をしたい、コンペでの精度を上げたいが、どんなモデルを使えばよいか分からない。最近そのように思っていたとき、「Papers With Code」というサイトを見つけました。

Papers With Code では、物体検知や、画像分類、画像生成などなど、様々な分野における最新手法の論文と実装コード（githubで公開）が掲載されています。
例えば、物体検知だとCOCOデータがベンチマークとしてよく用いられますが、COCOに対しての精度がランキング化されていて、今一番精度の良いモデルを調べることができます。
なので、手元のタスクデータをCOCOの形に整えておけば最新の手法について試すことができるということです。（実際はそんなに簡単ではないかもしれませんが。。）

これからどんどん活用していこうと思います！

参考にした書籍

本記事を作成するにあたって以下の書籍を参考にしました。
非常にわかりやすく理解が深まりました。

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
[[第3版]Python機械学習プログラミング 達人データサイエンティストによる理論と実践]
(https://www.amazon.co.jp/%E7%AC%AC3%E7%89%88-Python%E6%A9%9F%E6%A2%B0%E5%AD%A6%E7%BF%92%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E9%81%94%E4%BA%BA%E3%83%87%E3%83%BC%E3%82%BF%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%83%86%E3%82%A3%E3%82%B9%E3%83%88%E3%81%AB%E3%82%88%E3%82%8B%E7%90%86%E8%AB%96%E3%81%A8%E5%AE%9F%E8%B7%B5-impress-gear/dp/4295010073/ref=asc_df_4295010073/?tag=jpgo-22&linkCode=df0&hvadid=342595526565&hvpos=&hvnetw=g&hvrand=15773796937735192064&hvpone=&hvptwo=&hvqmt=&hvdev=c&hvdvcmdl=&hvlocint=&hvlocphy=1009283&hvtargid=pla-934396349943&psc=1&th=1&psc=1)