連続確率分布をJulia言語で復習だー＼(^o^)／(#Julialang)

(註)ひさしぶりにQiitaを開いたらどうやら6年前に途中で挫折してお蔵入りになった謎のテンションの黒歴史が発掘されたので限界中年男性の過ちと思って許して欲しい（公開しちゃいます）

はじめに

やっぷー、きむりんだょ。小六女子のつもりのおっさんだよ！
（ここで一同失笑w）

いや〜昨今のDeepなんとかブームとか、ベイズがどうこうとかで
結構確率分布を仮定することがあり意外と確率バカにできませんねぇ、
みたいな感じなんですが皆さん確率分布には詳しいですか？

2018/01頃にqiitaでも話題になったJulia言語で
簡単に確率分布を復習しちゃいましょ〜＼(^o^)／

あとJulia言語をJuliaで検索するとすっぽんぽんのおナィさんが出ちゃう
問題ってのがあって、Julia言語で検索するときはJulialangって言う
Twitterのハッシュタグと同じ単語で検索してね、大きなお友達との約束だぞっ♡

Julia言語そのものについてはJuliaタグでqiita内をストーカーしてね（？）

そもそもこの文章を書く目的とは

いえね、僕、機械学習の仕事をすることになって、で、とてもいい本を見つけたので
それを英語なんだけどヒーコラヒーコラ読んでましてね、で２章が確率の話なんですが、
こう言う本って結構ハイパーパラメーターとか出てくるんですがいまいち
「ガウス分布の式テクニカルでわかんねー＼(^o^)／」って、ガウス分布で
もう白旗って感じじゃないですか。

この本です！！！！

Machine Learning: A Probabilistic Perspective (Adaptive Computation and Machine Learning series) Kevin P. Murphy (著)

そこでJuliaですよ！　Julia言語なら！！　主要な確率分布が！！　簡単に！！
計算できちゃうんです！！！

Juliaで書くと正直バカッぱやでしてね、とある確率分布の乱数生成とかコーディングが秒でできちゃって、
もうハッピーハッピーなんですよ。

君もこのビックウェーブに乗るしかない！！　乗ってドンブラコドンブラコするしかない！！！

そもそも確率分布ってナニ？

おーい、そこからか〜＼(^o^)／

いいぞいいぞ、そこから説明しよう！！

まずcdfとpdfの話をしマーシュ！

pdfってアレでしょ、ドキュメントのフォーマットでしょ？？　なんで確率に関係あるの？

違うんです！！　そっちのpdfじゃなーい！！
もうね、「おねいさん、それは、卵かけご飯じゃ、ぬわ〜い（ニャンちゅうの声で）」ですよ！！

まずcdf、それからpdfの話から始めます！！
確率分布はpdfの種類で表現できるのです。

cdf (cumulative distribution function)

あんなこといいな、こんなこといいな、ってわけでこんな関数考えます。
とりあえず連続量の変数をテキトーに考えてXと置きます。
例えば平均50点の100点満点のテストとかを考えます。まぁ離散量なんですが、
この点数を小数点以下まで変えられることにして、今は連続量として捉えましょう。

その時、「50点以下の確率」を考えます。
つまり 50点以下の確率 = $p(X\leq$ 50)です。

とりあえず確率なので変数Xの取りうる範囲で総和が1にならないといけません。
あと確率なので$(0\leq p(X) \leq 1)$ っすよね。

おっと話がごちゃごちゃになってきたぞ。cdfに戻りましょう。

• $p(X = 0) = 0$
• $p(X \leq 50) = 0.5$
• $p(X \leq 100) = 1.0$

みたいになる関数を考えます。つまり「俺は$X_1$点なんだけど、俺より下は$P_1$割なんだ」って
言う関数を考えます。0点なら0、50点なら0.5（つまり全体の半分）、100点なら1.0（つまり全体）
です。つまりこんなグラフです（ガウス分布のcdfです）。

種明かしをするとcdfは次に紹介するpdfの積分です。
pdfがマイナスになることがないので、cdfは単調増加をします。つまり減少する箇所がありません。
反対にpdfは減少することもあります。と言うかほとんどの場合Xが極めて大きくなると0に近づきます。

pdf (probability density function)

一般的に連続量の確率密度関数と言うのはこのpdfのことです。

ガウス分布だと50点が平均なので50点の所にピークがあります。で、末広がりに高い方と低い方に
点数が分布しています。どこに点数が集中しているか、になります。

このベルカーブ（ガウス分布のこの曲線のことをそう言います）について端っこからもう一方の端っこまで積分すると1になります。
ここから逆にcdfは

$cdf(\beta) = \displaystyle \int_0^\beta pdf(x) dx$
特に$cdf(X=100) = \displaystyle\int_0^{100} N(50,10)dx \simeq 1$
ですね。ここでガウス分布のpdfのことを$N(\mu, \sigma^2)$と書きます。

つまりpdfが判ればどんな確率分布かわかる！

です。pdfからcdfも自動的に計算できます。
あとは分布の違いというものはpdfの式の違いとなります。
離散量の場合、pdfではなくpmfという表現になります。

Julia言語では。。。

Distributions.jl というパッケージを使うことでこのpdfやcdfを簡単に計算することができます。
しかもたった数行で！！

Julia言語準備

まずJuliaのコマンドラインで（あるいはJuno内から）

Pkg.update()
Pkg.add("Plots")
Pkg.add("PyPlot")
Pkg.add("GR")
Pkg.add("UnicodePlots")
Pkg.add("PlotlyJS")
Pkg.add("StatPlots")
Pkg.add("PlotRecipes")
Pkg.add("Distributions")

などとしてパッケージをインストールしてください。色々余計なものも入っていますが、
これでStatPlots.jlを使うと確率分布が簡単にプロットできます。あとある種の伝統なのですが、
パッケージ名には.jlをつけます。Pkg.addに渡すときは.jlは外します。

Dist.jl

using Distributions
using StatPlots

x = linspace(0.0, 100.0, 10000)
normal = Normal(50.0, 10.0)
y = cdf(normal, x)

pl = plot(x, y, title="cdf of examination")

y2 = pdf(normal, x)

pl2 = plot(x, y2, title="pdf of examination")

savefig(pl, "cdfnormal.png")
savefig(pl2, "pdfnormal.png")

先ほどのグラフ（cdf, pdf)もこれで書いてます。

まず区間をlinspaceで指定します。これは0から100まで10000分割です。
次にnormalという変数に確率分布（univalue)を渡します。
ガウス分布（正規分布）はNormalというクラスです。パラメーターの$\mu$と$\sigma^2$を
渡します。

Julia言語は何でもかんでも関数で直接アクセス、が基本です。cdfについてはcdf関数に分布と範囲を
渡すとplotに渡せる形になります。
そしてplot関数で確率密度関数(pdf)とcdfを書いて、pngファイルに落とします。簡単ですね。

確率分布、集合！！

Gaussian (normal) distribution

pdfは次式です〜
非常によく使われます。

$ f(x; \mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left( - \frac{(x - \mu)^2}{2 \sigma^2} \right)$

cdf

pdf

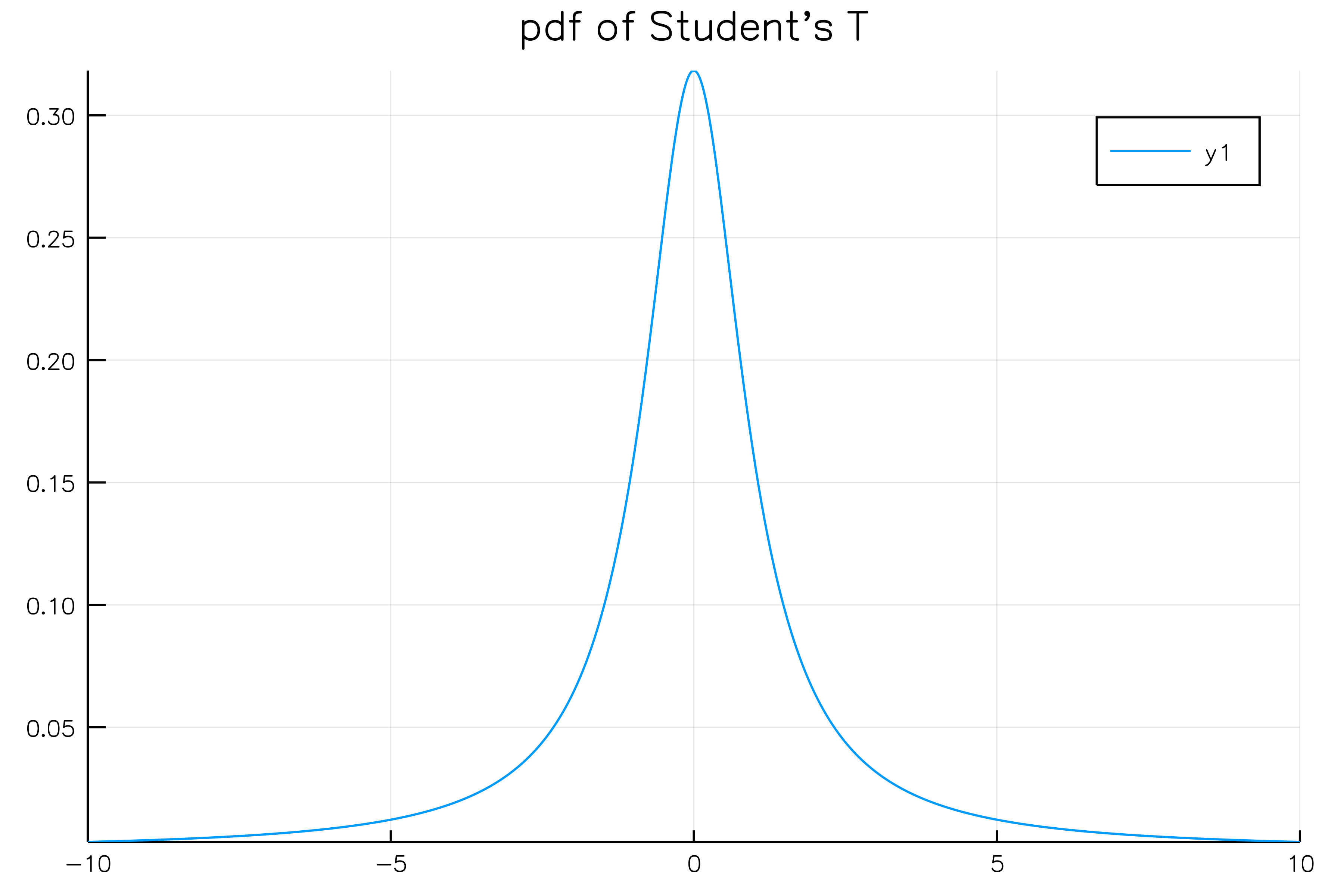
The Student’s t distribution

Gaussianよりもうちょっとゆるく減衰するpdfを持つものにStudentというものがあります。

$\displaystyle f(x; d) = \frac{1}{\sqrt{d} B(1/2, d/2)} \left( 1 + \frac{x^2}{d} \right)^{-\frac{d + 1}{2}}$

cdf

pdf

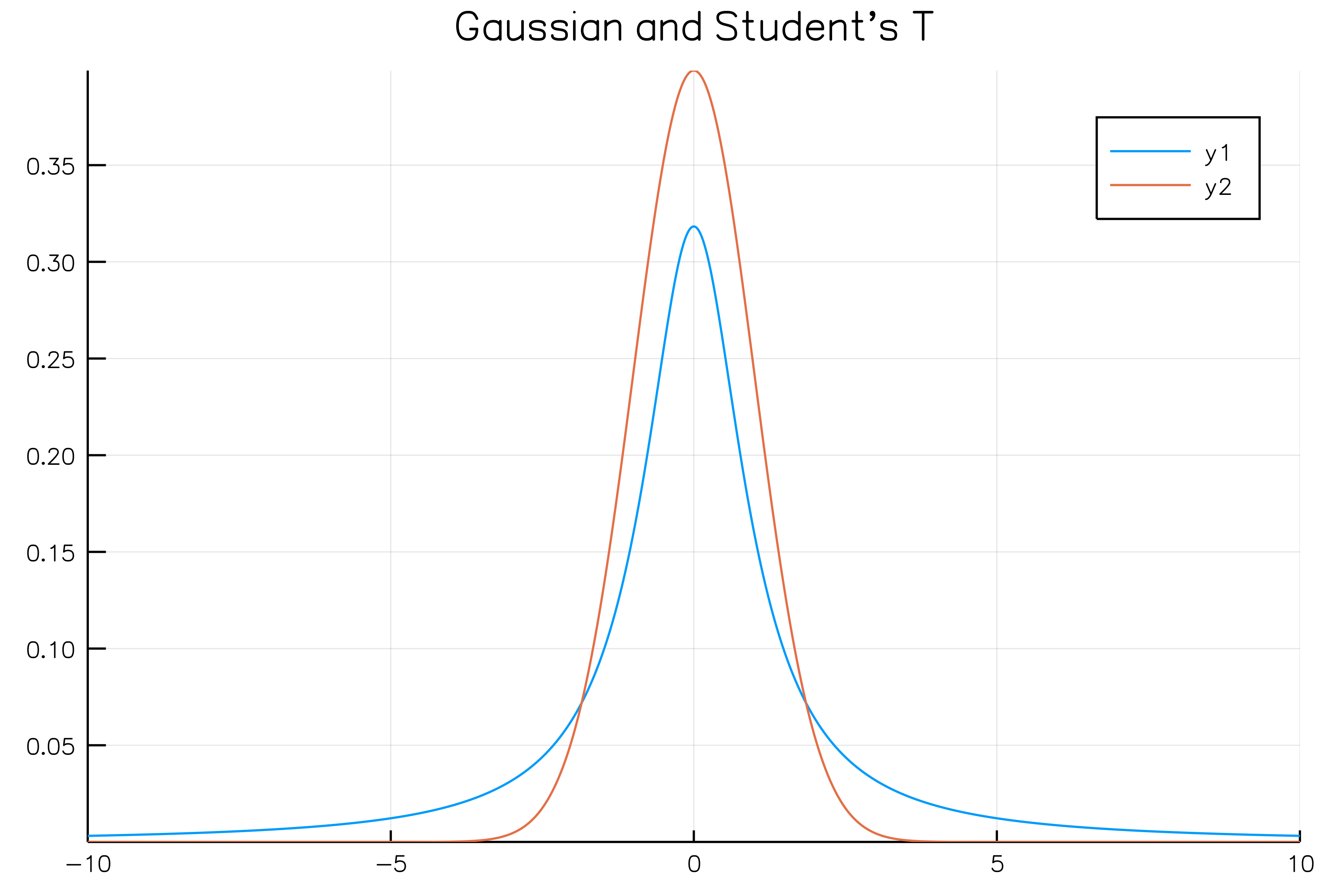
Gaussianのpdfと比較すると。。。

Studentの方が裾が広がっているのがわかります。

The Laplace Distribution

もうちょっと急峻なのにLaplaceというのがあります。pdfは次の通り。

$\displaystyle f(x; \mu, \beta) = \frac{1}{2 \beta} \exp \left(- \frac{|x - \mu|}{\beta} \right)$

cdf

pdf

上記三つのpdfを重ねると

The Gamma Distribution

$\displaystyle f(x; \alpha, \theta) = \frac{x^{\alpha-1} e^{-x/\theta}}{\Gamma(\alpha) \theta^\alpha},\quad x > 0$

Gamma(1,1)は次の通りです。$x > 0$dで定義します

cdf

pdf

The Beta Distribution

$\displaystyle f(x; \alpha, \beta) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1}, \quad x \in [0, 1]$

Beta(0.1, 0.1)[青]とBeta(8,4)[赤]はそれぞれ次の通りです。
$x \in [0, 1]$で定義します。$\alpha, \beta = 1$だとUniform、$\alpha, \beta < 1$だとピークが0と1に二つ、$\alpha, \beta > 1$だとピークが一つ、という特徴を持ちます。

cdf

pdf

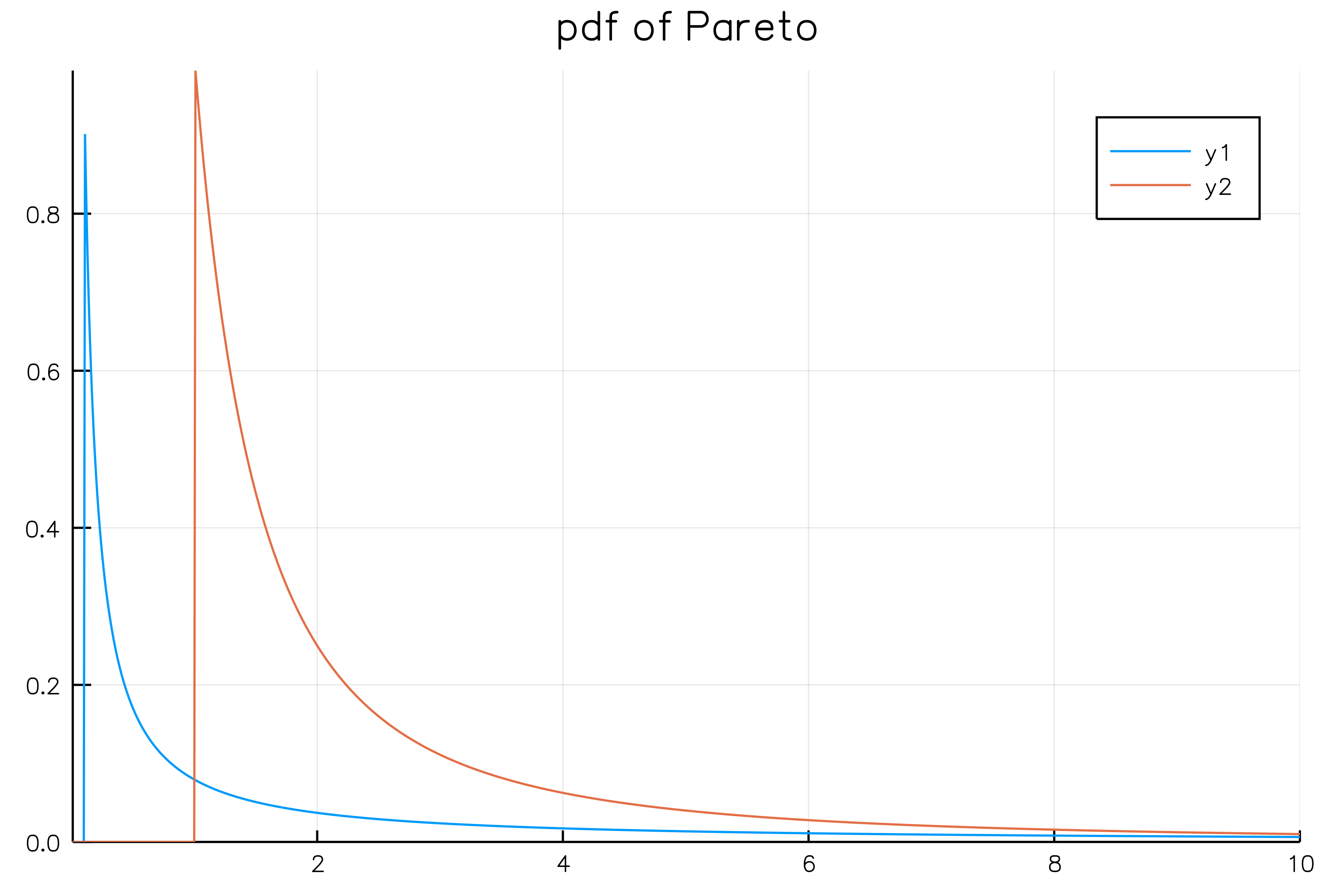
The Pareto Distribution

$\displaystyle f(x; \alpha, \theta) = \frac{\alpha \theta^\alpha}{x^{\alpha + 1}}, \quad x \ge \theta$

Zipf's law というのがParetoの特殊系のようです。
Pareto(0.1,0.1)[青]とPareto(1,1)[赤]は次の通りです。

cdf

pdf

Dirichlet distribution

今まではxが一つの値のものだけ扱いましたが、今度はいくつも$x_i$みたいに与えらえる
分布を考えます。Dirichlet分布はBetaのmultivalue版で、pdfは次の通りです。

$\displaystyle f(x; \alpha) = \frac{1}{B(\alpha)} \prod_{i=1}^k x_i^{\alpha_i - 1}, \quad \text{ with } B(\alpha) = \frac{\prod_{i=1}^k \Gamma(\alpha_i)}{\Gamma \left( \sum_{i=1}^k \alpha_i \right)}, \quad x_1 + \cdots + x_k = 1 $