水溜りボンドがやっていたマーチンゲール法をPythonで検証した

【本日の配信】

【マーチンゲール法】カジノで禁止された絶対に勝つ方法が凄すぎた！！https://t.co/pbftt39GVr pic.twitter.com/QT4ZD76l4q

— カンタ(水溜りボンド) (@kantamizutamari) 2019年1月13日

この動画で紹介されていたマーチンゲール法をPythonで試してみました。

マーチンゲール法とは？

マーチンゲール法とは絶対にペイできるという、18世紀のフランスで発明されたカジノでの必勝法です。
勝ったら2倍になるギャンブルで、

1. $1賭ける
2. 負けたら、さらに$2賭けて再挑戦する
3. それでも負けたら、$4賭けて再挑戦……
4. 連続$n$回負けたら$$2^n$賭けて再挑戦

こうやっていけばいつかはペイできる戦略ということです。
カジノ側はこの対策を施していて今はできないとか……

Pythonで実装する

コードの変数等は日本語で書きました。TOEIC帰りで英語を書く気分じゃなかったので……

martingale.py

import random

万 = 10000
所持金 = 2000*万
色の種類 = ["赤", "黒"]
回数 = 0

def 賭ける(金額): 
    global 回数
    global 所持金
    回数 += 1 # 賭けた回数をカウント
    if 所持金 < 金額: # 所持金が足らない場合
        print("もう賭けられません") 
        print("所持金: {0:,} 賭けようとした金額: {1:,}".format(所持金,金額))
        return False
    所持金 -= 金額 # 所持金から賭けたお金は差っ引く

    色 = random.choice(色の種類) # 賭ける（赤か黒から半々）
    if 色=="赤": # カンタ君は赤を選び続けました
        所持金 += 金額*2 # 勝ったので2倍のお金をもらう
        print("勝ちました！")
        print("所持金: {0:,} 賭けた金額: {1:,}".format(所持金,金額))
        return True
    else:
        print("負けました！")
        print("所持金: {0:,} 賭けた金額: {1:,}".format(所持金,金額))
        print("{0:,}円 賭けます".format(金額*2))
        return 賭ける(金額*2) # 2倍さらに賭ける

賭ける(100*万)

おのれRouge An elegant, extendable code highlighter written in pure Ruby！
今の俺に英語用のスペルチェッカーなど必要ないのだ！

関数「賭ける」は、グローバル変数の所持金から指定額を抜き取ります（もし抜き取れない＝金が無かったら破産します）。負けたらその二倍を賭け直します。
所持金は、動画と同じ2000万円、最初に賭ける金額は100万円とします。

このプログラムを何度か実行してみた結果がこちらです。

[Running] python -u "/Users/adam/Documents/snippets/martingale.py"
勝ちました！
所持金: 21,000,000 賭けた金額: 1,000,000

[Done] exited with code=0 in 0.147 seconds

[Running] python -u "/Users/adam/Documents/snippets/martingale.py"
負けました！
所持金: 19,000,000 賭けた金額: 1,000,000
2,000,000円 賭けます
負けました！
所持金: 17,000,000 賭けた金額: 2,000,000
4,000,000円 賭けます
負けました！
所持金: 13,000,000 賭けた金額: 4,000,000
8,000,000円 賭けます
負けました！
所持金: 5,000,000 賭けた金額: 8,000,000
16,000,000円 賭けます
もう賭けられません
所持金: 5,000,000 賭けようとした金額: 16,000,000

[Done] exited with code=0 in 0.171 seconds

[Running] python -u "/Users/adam/Documents/snippets/martingale.py"
負けました！
所持金: 19,000,000 賭けた金額: 1,000,000
2,000,000円 賭けます
勝ちました！
所持金: 21,000,000 賭けた金額: 2,000,000

[Done] exited with code=0 in 0.185 seconds

一発で勝つ場合もあるのですが、4回負け続けただけで死ぬ場合もあるということがわかるかと思います。
ただ、4回のうちのどこかで勝てばいいというのは大きいでしょう。

2000万円を4000万円にするには？

せっかくなので、これで2000万円の二倍、4000万円を稼いでみましょう。

while 所持金 < (4000*万): # お金が二倍=4000万円になるまで
    結果=賭ける(100*万)
    if not 結果: # 破産したら終わり
        break

[Running] python -u "/Users/adam/Documents/snippets/martingale.py"
負けました！
所持金: 19,000,000 賭けた金額: 1,000,000
2,000,000円 賭けます
勝ちました！
所持金: 21,000,000 賭けた金額: 2,000,000
勝ちました！
所持金: 22,000,000 賭けた金額: 1,000,000
負けました！
所持金: 21,000,000 賭けた金額: 1,000,000
2,000,000円 賭けます
勝ちました！
所持金: 23,000,000 賭けた金額: 2,000,000
負けました！
所持金: 22,000,000 賭けた金額: 1,000,000
2,000,000円 賭けます
負けました！
所持金: 20,000,000 賭けた金額: 2,000,000
4,000,000円 賭けます
負けました！
所持金: 16,000,000 賭けた金額: 4,000,000
8,000,000円 賭けます
負けました！
所持金: 8,000,000 賭けた金額: 8,000,000
16,000,000円 賭けます
もう賭けられません
所持金: 8,000,000 賭けようとした金額: 16,000,000

[Done] exited with code=0 in 0.175 seconds

破産してしまいました。
4000万円を貯めるまでに破産する確率を出してみましょうか

破産件数=0
for i in range(1000):
    所持金 = 2000*万 # 所持金リセット
    while 所持金 < (4000*万): # お金が二倍=4000万円になるまで
        結果=賭ける(100*万)
        if not 結果: # 破産したら終わり
            破産件数+=1 # 破産したら破産件数一件追加
            break

print("破産率: {}%".format(破産件数/10)) # 確率を求める(総件数が1000で、パーセンテージなので破産件数/10)

破産率: 61.9%

ええ……
マーチンゲール法は手元のお金が重要なので、さすがに全財産を二倍にするようなことはきついようです。

所持金の変遷をグラフにする

マーチンゲール法では、あのカジノにあるぐるぐるを何回回す必要があるのでしょうか。
これを調べるために全体的に書き直しました。

martingale.py

import random
import matplotlib.pyplot as plt # グラフを書くライブラリ
import seaborn as sns # お好みでグラフをスタイリッシュにする

万 = 10000
所持金 = 2000*万
色の種類 = ["赤", "黒"]
回数 = 0
賭けた時の所持金の変遷=[] # 変遷表を追加

def 賭ける(金額):
    global 回数
    global 所持金
    回数 += 1 # 賭けた回数をカウント
    賭けた時の所持金の変遷.append(所持金) # 所持金を記録
    if 所持金 < 金額: # 所持金が足らない場合
        print("もう賭けられません") 
        print("所持金: {0:,} 賭けようとした金額: {1:,}".format(所持金,金額))
        return False
    所持金 -= 金額 # 所持金から賭けたお金は差っ引く

    色 = random.choice(色の種類)
    if 色=="赤":
        所持金 += 金額*2 # 勝ったので2倍のお金をもらう
        print("勝ちました！")
        print("所持金: {0:,} 賭けた金額: {1:,}".format(所持金,金額))
        return True
    else:
        print("負けました！")
        print("所持金: {0:,} 賭けた金額: {1:,}".format(所持金,金額))
        print("{0:,}円 賭けます".format(金額*2))
        return 賭ける(金額*2) # 2倍さらに賭ける

while 所持金 < (4000*万): # お金が二倍=4000万円になるまで
    結果=賭ける(100*万)
    if not 結果: # 破産したら終わり
        break
plt.plot(range(回数), 賭けた時の所持金の変遷)
plt.savefig("martingale/所持金変遷.png")
# plt.show()

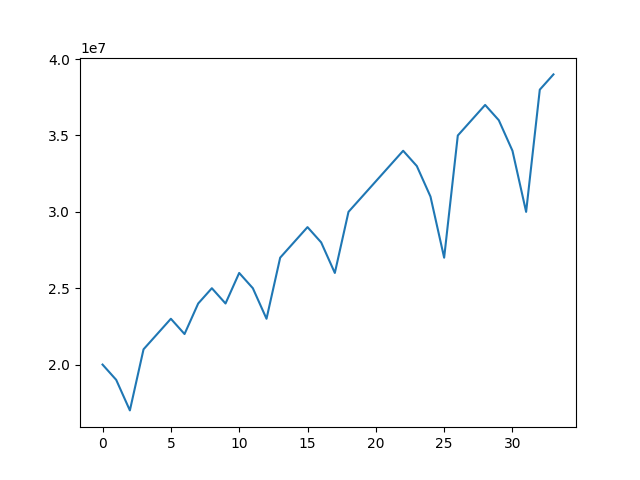
これで何度か試してみて、一番綺麗に撮れていたのがこれなのでこれで説明します。

これは4000万円（$=4 \times 10 ^ 7$）に到達するまでのグラフです。どうやら、35回ぐらい回せば2000万円獲得できるようですね。

このグラフには、右肩上がりの部分と、谷状に落ち込んでいる部分があることがわかります。
この谷状の部分はドツボにはまっているところですが、マーチンゲール法のポジティブな面により一発で抜け出しています。

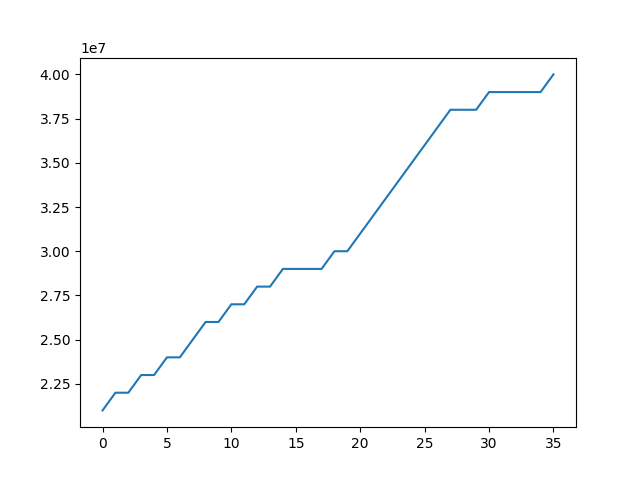
この谷を潰して表示してみましょう

# (略)
def 賭ける(金額):
    global 回数
    global 所持金
    回数 += 1 # 賭けた回数をカウント
    # 賭けた時の所持金の変遷.append(所持金) # 所持金を記録
    if 所持金 < 金額: # 所持金が足らない場合
# (略)

前回までの回数=0
while 所持金 < (4000*万): # お金が二倍=4000万円になるまで
    賭ける前の所持金=所持金
    結果=賭ける(100*万)
    for i in range(前回までの回数,回数-1):
        賭けた時の所持金の変遷.append(賭ける前の所持金) # 配列を賭ける前の所持金で埋める
    賭けた時の所持金の変遷.append(所持金) # 賭けた時の所持金を追加
    前回までの回数=回数
    if not 結果: # 破産したら終わり
        break
plt.plot(range(回数), 賭けた時の所持金の変遷)
# plt.show()
plt.savefig("martingale/所持金変遷2.png")

こうするとわかりやすいと思うのですが、仮に手持ちのお金が追いついていたとしても、最大の傾きは常に同じです。
最大でも1ベット100万円しか儲けられないということがわかります。
だからカンタ君はめちゃくちゃつまらなさそうだったのですね。

マーチンゲール法を使えば、資産があればほぼ確実に2000万円を手にすることができますが、実際にカジノでやるとなると、30回ほど回さなければなりません。
もっと言えば、金が10倍になるかスッカラカンになるかと同伴者がドキドキしながら、指数関数レベルの戦いを演じている側で、コンスタントに金を稼いでいくのはあまりにもつまらないかと思います。
しかも途中途中落ちて復帰している間は稼げないので、一次関数以下のスピードとなります。

そう考えると、カジノがマーチンゲール法を禁じたのは、店が儲けられないからよりも客が楽しめないからではないでしょうか。

Pythonの宣伝

以上のように、プログラミングを学んでおくと、日常でふと疑問に思ったことを検証するために便利です。
中でもPythonは、Numpy（数値計算）やMatplotlib（グラフ）などの、疑問を解決するのに便利なライブラリがたくさん揃っています。
ということで、あなたもPythonを学んでみませんか？

なお私はJavaScript派です。