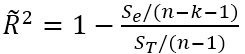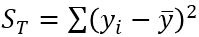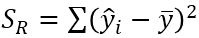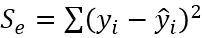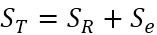【R】線形回帰分析

#統計モデルと回帰分析
統計モデルの説明のため、身近な例として、身長と体重との関係をなんらかの式で表すことを考えることにする。その具体的な関係がわからないので、抽象的な関数記号$f$で次のように表すことにする。

体重 = f(身長)

この式の中の「身長」を説明変数、「体重」を被説明変数、あるいは目的変数と呼ぶ。もし説明変数を$x$、被説明変数を$y$で表すと上記の式は次のような式になる。

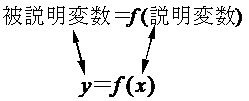
このような説明変数を用いて被説明変数を説明する関係を求める統計モデルを通常回帰分析と呼ぶ。説明変数が1つの場合は単回帰分析、説明変数が複数の場合は重回帰分析と呼ぶ。

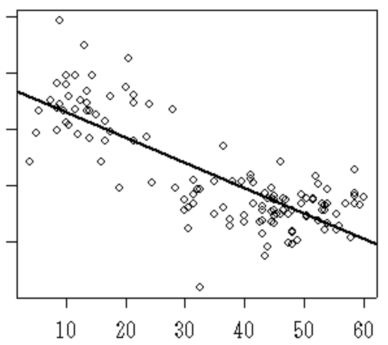
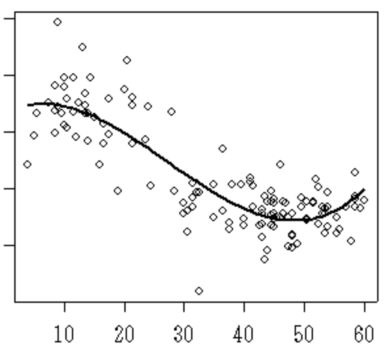
単回帰分析の例として2種類の説明変数と被説明変数の関係を示す。横軸が説明変数、縦軸が被説明変数である。
左下図では、説明変数と被説明変数との関係を直線で大まかな傾向を示している。このような直線関係でモデル化する回帰分析を線形回帰分析と呼ぶ。
右下図の説明変数と被説明変数のような非直線的関係でモデル化する回帰分析を非線形回帰分析と呼ぶ。

#線形単回帰分析とは
線形単回帰分析とは説明変数が一つである回帰分析のことであり、単回帰分析と略される。
説明変数を$x$、非説明変数を$y$としたとき次の関係式で表すことができる。

y = a + bx

式の中の$a$を切片、$b$は直線の傾きに関する値で、説明変数$x$の係数と呼ぶ。

###Rで分析する
####データの概要
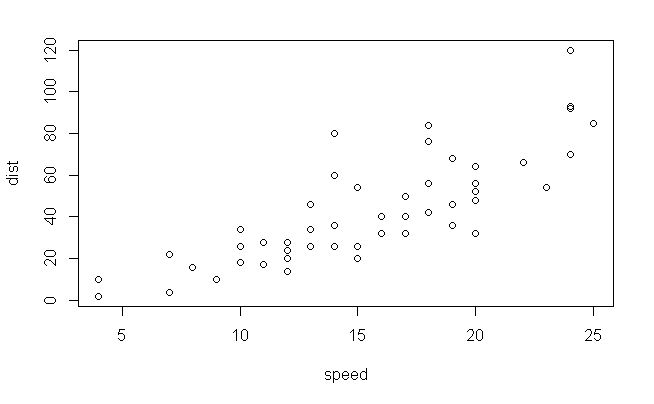
Rのデータセットcarsを用いる。これは車の速度とブレーキをかけた後、車が止まるまでの距離に関して50回の実験結果を記録した二変数のデータフレームである。

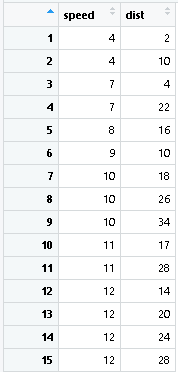
####両変数の相関関係を考察する。

plot(cars);cor(cars$speed,cars$dist)

実行結果
[1] 0.8068949

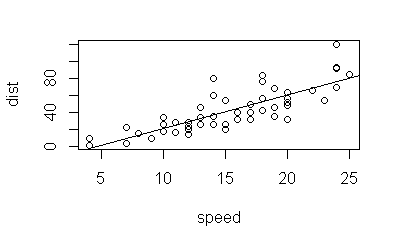
以上から、相関係数は約0.8で、散布図から線形関係があることが読み取れるので、単回帰分析を適用する。

####分析
speedを説明変数、distを目的変数として線形回帰関数lmを用いて分析する。

cars.lm <- lm(dist~speed,data=cars)
summary(cars.lm) #結果を次図に示す

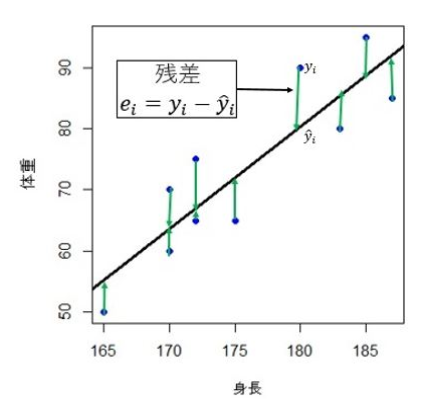
#####(1)残差
データ(真のモデル)を
$y_i = a + bx_i + e$
回帰直線(予測モデル)を
$\hat{y_i} = a + bx_i$
としたとき、説明変数$x$が$x_i$をとった場合の両値の差である$e_i = y_i - \hat{y_i}$を残差(residuals)と呼ぶ。次図にデータ、回帰直線、残差を示す。

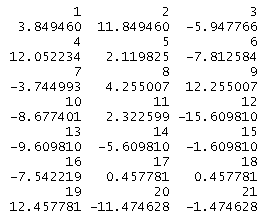
つまり、summaryのResidualsでは残差の最小値、第一四分位数、中央値、第二四分位数、最大値が返される。次のコマンドですべての残差を確認することができる。

residuals(cars.lm)

#####(2)回帰式と回帰係数
回帰直線$\hat{y} = a + bx$の係数(Coefficients)である$a$、$b$は残差の二乗和

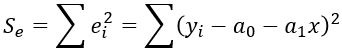
を最小化する連立方程式を解くことで次の解が得られる。

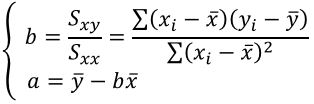
上記のsummaryで返されている結果の Coefficients の部分が回帰係数及びそれに関連する情報である。Interceptの行が切片$a$の推測値、その標準誤差、$t$値、$p$値である。その次の行が説明変数「speed」の係数と関連の情報である。
　回帰式は返されている回帰係数を用いて次のように構築する。
dist = -17.5791+3.9324*speed
回帰係数の標準誤差、$t$値は次の式で定義される。式中の$n$はデータの標本数、$k$は説明変数の数である。
残差の平方和: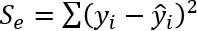　　
残差の不偏分散: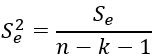　
係数$a$の標準誤差: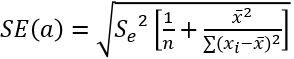　　
係数$b$の標準誤差: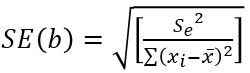　
係数$a$の$t$値: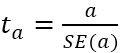　
係数$b$の$t$値: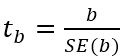

この$t$値は「回帰係数がゼロである」という仮説検定の統計量である。$p$値が通常よく使われている有意水準0.05(5％)、0.1(10％)、0.05(0.5％)より小さいときには、出力結果の$p$値の右にそれぞれ1つの星“”,2つの星“”、3つの星“”で印をつける。
次のコマンドで回帰係数を確認することができる。

coefficients(cars.lm)

実行結果
(Intercept) speed
-17.579095 3.932409

#####(3)決定係数
決定係数 (coefficient of determination)は回帰直線がどの程度データにフィットしているかを評価する指標である。通常は$R^2$で示す。
関数lmでは決定係数 (Multiple R-Squared) と調整済み決定係数 (Adjusted R-squared) が返される。決定係数と調整済み決定係数が1に近づくほど回帰直線がデータによくフィットしていると判断する。
決定係数と調整済み決定係数は次の式で定義されている。式の中のn は標本の数で、ここのk は説明変数の数である。単回帰では説明変数が１つであるのでk =1 である。
決定係数: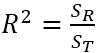　

調整済み決定係数:　

決定係数と調整済み決定係数の両方が出力されてる場合は、調整済み決定係数の方を参考にするとよい。

y偏差の平方和:　

$\hat{y_i}$偏差の平方和:　

残差の平方和:　

平方和の関係:　

#####(4)予測値
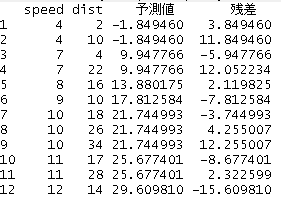
関数predictを用いて、回帰式で計算される値である予測値を返す。一覧表にすると見やすい。

予測値<-predict(cars.lm)
残差<-residuals(cars.lm)
data.frame(cars,予測値,残差)

#####(5)グラフによる分析
説明変数と目的変数の散布図に求めた回帰直線を加えることでデータの傾向を可視化することができる。

plot(cars)
abline(cars.lm) #散布図に回帰直線を追加する

残差を視覚的に分析する。

op <- par(mfrow=c(2,2))
plot(cars.lm)
par(op)

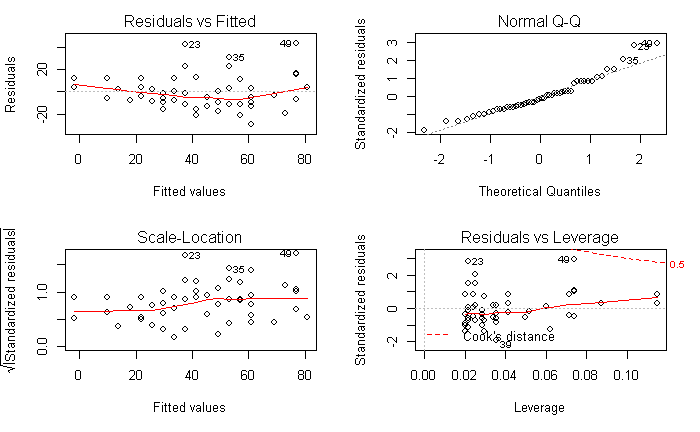
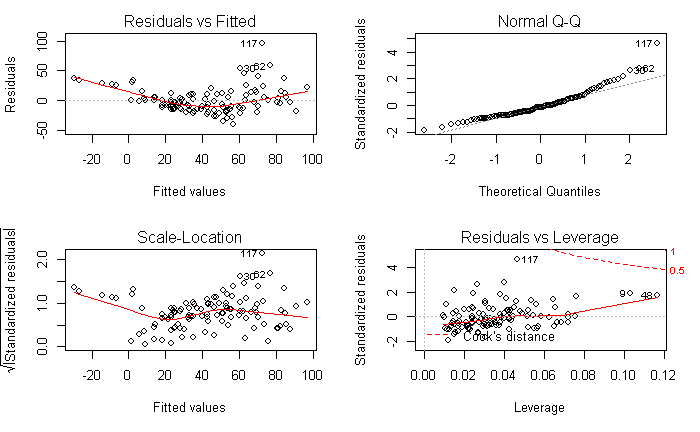
①残差とフィット値のプロット
左上図は残差とフィット値の散布図である。ここで言うフィット値は予測値である。図の横軸が予測値、縦軸が残差となっている。図から残差の全体像を概観することができる。この図では個体 23、35、49 の残差が相対的に大きいことがわかる。

②残差の正規Q-Qプロット
右上図は標準化した残差のQ-Qプロットである。正規Q-Qプロットはデータの正規性を考察するためにデータを視覚化する方法である。データが正規分布に従うと、点が直線上に並べられる。通常の回帰分析では、残差が標準正規分布に従うという仮定の下で行っている。Q-Qプロットから大きく乖離した固体がある場合はそれを除いて回帰モデルを作成しなおす必要がある。

③残差の平方根プロット
左上の図と基本的には同じである。縦線が標準化残差の平方根である。

④梃子値とCookの距離のプロット
右下の図は、当てはまりの良すぎるデータを評価する指標として用いられる梃子値とCookの距離のプロットである。回帰分析では、通常なデータにおいては当てはまりが良すぎるデータが多くても、当てはまりが悪すぎるデータが多くても望ましくない。
横軸が梃子値で赤い点線でCookの距離の目安を示している。Cookの距離が目安より大きい固体がある場合は、それを除いて回帰モデルを作成し直す必要がある。

#線形重回帰分析とは
説明変数が複数ある回帰分析を重回帰分析と呼ぶ。重回帰分析では観測データが次の式で表現できることを前提としている。

$ y = a_0 + a_1x_1 + a_2x_2 + .... + a_nx_n + ε$

回帰分析で求める回帰式は次に示すような式である。
$ \hat{y} = a_0 + a_1x_1 + a_2x_2 + .... + a_nx_n$

###Rで分析する
####データの概要
データセットairqualityを用いる。これは1973年5月から9月までのニューヨークの大気状態を6つの変数で観測・記録したものである。

[,1] Ozone　　　オゾンの量
[,2] Solar.R　　太陽の放射の量
[,3] Wind　　　 風力
[,4] Temp　　　 温度
[,5] Month　　　月：1～12
[,6] Day　　　　日：1～31

ここでは、オゾンの量を目的変数、太陽の放射の量、風力、温度を説明変数とする重回帰モデルを作成する。

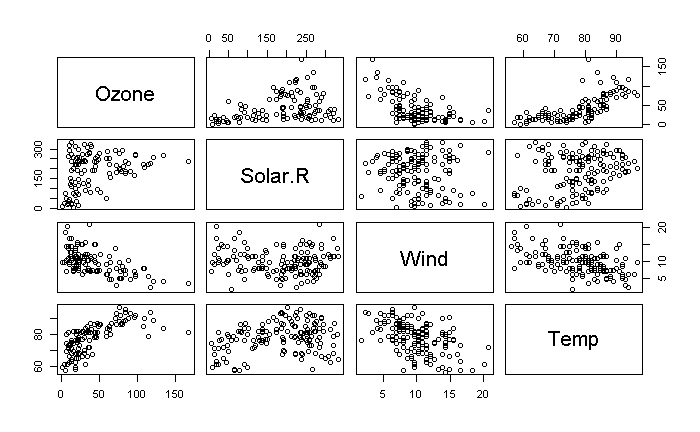
####両変数の相関関係を考察する。

pairs(airquality[,1:4])

出力結果

オゾン量は、風力および温度とやや強い相関があることが読み取れる。

####分析
オゾンの量を目的変数、太陽の放射の量、風力、温度を説明変数とする重回帰モデルを作成する。単回帰分析と同様lm関数を用いる。

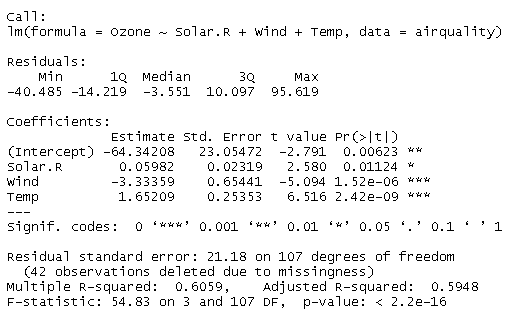
air.lm <- lm(Ozone~Solar.R+Wind+Temp,data=airquality)
summary(air.lm)

出力結果

回帰式は Ozone = -64.34 + 0.06 * Solar.R -3.33 * Wind + 1.65 * Temp　となる。

#####(1)多重共線性
重回帰分析のときは多重共線性について考察する必要がある。多重共線性とは目的変数と相関の高いいくつかの説明変数を選択し、説明変数同士の強い相関によって回帰モデルのなかで矛盾が生じる現象のことである。たとえば説明変数には強い相関があるのに回帰係数の符号が逆になる現象である。
チェックする方法として、モデルの分散拡大要因VIFの指標がある。一般的にはVIFの値が10より大きいと多重共線性の可能性が高いと言われている。

install.packages("car") #vifを使用するためのパッケージ
library(car)
vif(air.lm)

出力結果
Solar.R Wind Temp
1.095253 1.329070 1.431367

すべて2以下なので、多重共線性はない。

#####(2)残差分析

op <- par(mfrow=c(2,2))
plot(air.lm)
par(op)

117の残差が相対的に大きい。

#####(3)交互作用モデル
重回帰分析では、目的変数と説明変数間の相関関係のほかに、説明変数間にも関連性がある場合がある。airqualityでは風速と気温には相関関係があることが先ほどの散布図からも読み取れる。
このように説明変数間の関係が目的変数に影響することを交互作用とよぶ。あてはまりのよいモデル作成のためには、交互作用を考慮する必要がある。説明変数が2つである場合の一般式を示す。
$\hat{y} = a_0 + a_1x_1 + a_2x_2 + a_3x_1x_2$
Rでは交互作用を考慮した回帰係数を求めることができる。lm関数の中の**^2**が交互作用の指定である。

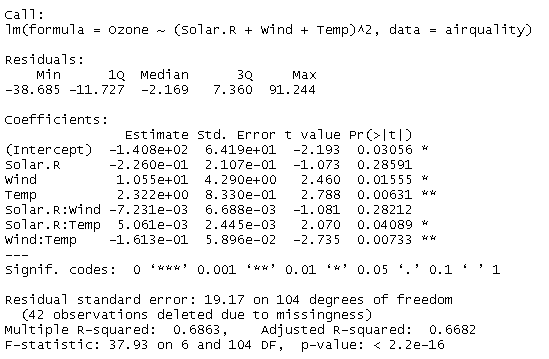
air.lm2 <- lm(Ozone~(Solar.R+Wind+Temp)^2,data=airquality)
summary(air.lm2)

出力結果

交互作用を考慮していない場合の決定係数は0.6059、調整済み決定係数は0.5948なので、交互作用を考慮したモデルの方が当てはまりがよいといえる。

#####(4)変数・モデルの選択
変数の選択では、説明変数を入れ替えながら回帰モデルを構築し、より当てはまりがよいモデルを採択する。そこで、モデルの選択基準として広く知られている、赤池弘次氏が提案したAICを用いる。AICは次の式で定義される。

$AIC = -2*(モデルの最大対数尤度) + 2*(モデルのパラメータ数)$

AICを用いてモデルを選択する場合は、AICの値が小さいモデルをあてはまりがよいと評価する。Rではstep関数を用いて変数選択をおこなう。step関数は増減法、増加法、減少法による変数の選択を、引数directionにそれぞれ"both", "forward", "backward"を指定することでできる。デフォルトでは増減法になっている。

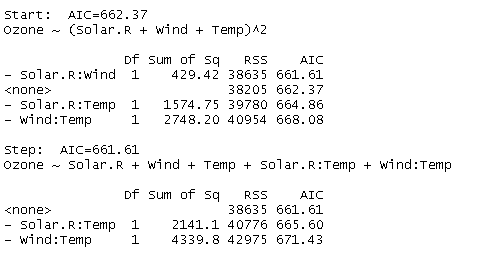
air.lm3 <- step(air.lm2)

出力結果

すべての変数の交互作用を考慮したモデルのAICは662.37であり、説明変数Solar.R:Wind(交互作用の変数)を除くと、AICの値が若干減り6661.61となり、これ以上AICの値が小さくならないので計算が終了する。
以上の結果から、AICで得られたモデルは次のようになる。

round(coefficients(air.lm3),2) #係数を出力する

出力結果

$Ozone = -136.81 - 0.35 * Solar.R + 11.15 * Wind + 2.45 * Temp + 0.01 * Solar.R * temp - 0.19 * Wind + Temp$

#####(5)再度多重共線性の確認

vif(air.lm3)

変数の値がすべて10を超えているので、回帰モデルとして採用することは難しい。なので、決定係数のみなど機械的に評価することは危険である。