PHPでハノイの塔

ハノイの塔をPHPで解く

問題

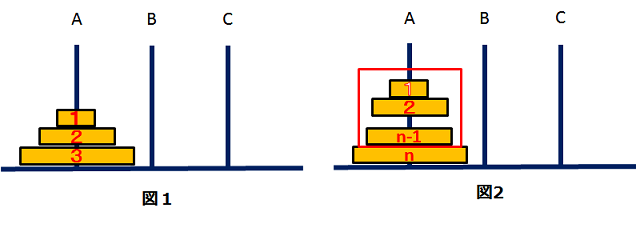
台の上に３本の棒 A，B，Cが固定されている。
うちの1本に何枚かの円盤が重ねられている。
円盤は下へいくほど半径が大きい。
この時、次の規則に従って，円盤をＡからBに移動する。

1. 1回に 1枚の円盤しか動かしてはいけない。
2. 移動の途中で円盤の大小を逆に積んではいけない
   　常に大きい円盤が下になるようにする
3. 棒 A，B，C以外のところには円盤を置けない

ポイント

　・小さい数で検証する事
　・分割統治法を使う事
　・正しい動作をする関数を定義する事
　・円盤のnを小さい順から定義する事

n=2の時の答え

　1. 1の円盤をAからCへ移動する
　2. 2の円盤をAからBへ移動する
　3. 1の円盤をCからBへ移動する

解き方

問題を小さい問題に分割して解く。
1～n-1の円盤を一塊にして
1～n-1の円盤とn番目の円盤の2つで考える。
ここで、関数を定義するhanoi($n, $a, $b, $c)
n枚の円盤を$aから$bへ移動する。$cが補助として使える
　
2枚の円盤の場合は
　hanoi($n-1, $a, $c, $b) = $n-1枚の円盤の塊を$aから$cへ移動する。補助として$bが使える
　次にn番目の円盤を$aから$bに移動する = f($n, $a, $b)
　次にhanoi($n-1, $c, $b, $a) = n-1枚の円盤の塊を$cから$bへ移動する。補助として$aが使える。
$aには何も無いから自由におけるし、$cの円盤は$bにある円盤よりも小さいので問題ない。
これで2枚の円盤の時は終了。

これを式で表すと
Hanoi($n, $a, $b, $c) = hanoi($n-1, $a, $c, $b) + f($n,$a, $b) + hanoi($n-1, $c, $b, $a)
後はこれをn=1まで再帰で解いてOK。

n=2の時の検証

①hanoi(2, “A”, “B”, “C”) = hanoi(1, “A”, “C”, “B”)
+ 2番目の円盤1をAからBへ移動
+ hanoi(1,”C”, “B”, “A” )

②hanoi(1, “A”, “C”, “B”) = hanoi(0, “A”, “B”, “C”)
+ 1番目の円盤をAからCへ移動
+ hanoi(0, “B”, “C”, “A”)

③hanoi(1, “C”, “B”, “A”) = hanoi(0, “C”, “A”, “B”)
+ 1番目の円盤をCからBへ移動
+ hanoi(0, “A”, “B”, “C”)
ここでhanoi(0,xx,xx,xx)の時は何もしない
①～③を合わせると (分割して最後に合わせる) = 分割統治
1番目の円盤をAからCへ移動
2番目の円盤をAからBへ移動
1番目の円盤をCからBへ移動
n=2の時はOK

コード

hanoi(2,"A", "B", "C");
echo '<br>';
hanoi(3,"A", "B", "C");

function hanoi($n, $a, $b, $c) {
    if ($n > 0) {
        hanoi($n-1, $a, $c, $b);
        echo $n .'番目の円盤を' . $a . 'から' .$b. 'に移動する';
        echo '<br>';
        hanoi($n-1, $c, $b, $a);
    }
}

コードとドキュメント