概要
2021年に日本初の商用量子コンピューターが設置されるなど、量子コンピューターの実用化への動きはますます大きくなっています。本記事では現在の実機で実装可能といわれる機械学習アルゴリズムであるQSVM(量子サポートベクターマシーン)を自然言語処理の問題に適用し、従来のSVM(サポートベクターマシン)との比較を行いました。なお、今回の実装では量子コンピューターの実機は使わずシミュレーターで実験しています。用いた題材はSMSの内容がスパムかどうかの2値分類です。"自然言語処理x量子コンピューター"という題材はあまり見かけなかったのでこのような問題設定にしてみました。
比較ではqiskitを用いた簡単な実装でQSVMはテストデータをscikit-learnによる実装のSVMと同等の精度で分類可能であることが確認できました。なお、今回は簡易的な正答率の比較のみであり、また私は機械学習の専門家ではないため比較手法に問題があるかもしれませんがあらかじめご了承ください。
SVM
SVMことサポートベクターマシンは教師あり機械学習の一種です。2種類の集団があったときにその集団を分割する直線(注:2次元の場合)を見つけるという考え方がベースにあります。ただしいつも直線できれいに分けれる集団ばかりではないので工夫を加えることで様々なモデルに対応可能になっています。SVMについての解説はネット上にたくさんあるため詳細は割愛しますが、この工夫を加えるときにカーネルと呼ばれる一種のハイパーパラメータが導入されます。このカーネルは学習モデルの作成者が問題に応じて選択をする必要があり使用したカーネルによって得られる結果が異なります。
SVMでは、直線で分割できないデータセットに対応するため、各サンプルを示すベクトル$\boldsymbol{x}_i$を別のベクトルに変換する写像$\phi(\boldsymbol{x}_i)$を用意し、マッピングした後の空間で分割を行います。一般にこの写像$\phi$によってマップされた空間は元のベクトルの空間よりも高次元になるため、計算量が増加します。一方、SVMで利用するのはベクトルの内積をとった後の値$\phi(\boldsymbol{x}_i)^T \cdot \phi(\boldsymbol{x}_j)$のみなのでわざわざ$\phi(\boldsymbol{x}_i)$を計算しなくとも$K(\boldsymbol{x}_i, \boldsymbol{x}_j)=\phi(\boldsymbol{x}_i)^T \cdot \phi(\boldsymbol{x}_j)$なる関数$K$(ベクトルではなく1つの値なので計算量が少ない)を計算すれば良いということになり、これをカーネルと呼んでいます。
同じデータに対して異なるカーネルを選択したときの境界の様子、scikit-learnのsvmのページより引用。
QSVM
QSVM(量子サポートベクターマシーン)はSVMの処理(の一部)を量子コンピューターに行うようなアルゴリズムの総称です。実装方法はいくつか提案されているようですが、本記事ではHavlicek et al.(2019)で提案された手法をベースにQiskit(量子コンピューターを操作したり量子アルゴリズムを実装するためのSDK)で実装されたライブラリを用いています。この手法ではQSVM/SVMでの処理の要となるカーネルの計算を量子回路上で行い、SVMで通常用いられるカーネル以上の表現力を得ようと試みます。
訓練データ
実験ではKaggleで公開されている迷惑メールのデータセットであるSMS Spam Collection Datasetを用いて検証しました。このデータセットにはスパムかどうかラベル付けされた5,574のSMSのサンプルが収録されており、教師あり学習に用いることができます。
実装
まずは必要なmoduleをimportします。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.svm import SVC
from qiskit import Aer
from qiskit.circuit.library import ZZFeatureMap
from qiskit_machine_learning.kernels import QuantumKernel
python, qiskit, scikit-learnのバージョンは以下のとおりです。
Python 3.9.12
qiskit-aer 0.10.4
qiskit-machine-learning 0.3.1
qiskit-terra 0.20.0
scikit-learn 1.0.2
文章データの整形
あらかじめダウンロードしておいた、kaggleのSMS Spamデータセットを読み込み、不要な列を落とすなどした処理を行います。データをみるとスパムの文章はspam, そうでなければhamと書いてあるのがわかります。
df = pd.read_csv('spam.csv', encoding='latin-1')
df.drop(['Unnamed: 2', 'Unnamed: 3', 'Unnamed: 4'], axis=1, inplace=True)
df.rename(columns={"v1":"class", "v2":"text"}, inplace=True)
df.head() #データの中身を見てみる
現状Qiskitでシミュレーターを用いて全ての訓練データで実行すると時間がかかってしまうため、データを選別します。また、Spamの文章は全体の1割程度なので、訓練データの偏りを抑えるために訓練データはspam/hamが半々になるようにサンプリングすることにしました。また、今回は訓練データ数を500, テストデータ数を100としています。
def spam_ham_ratio(df):
num_spam = df[df['class'] == 'spam'].count()['class']
num_ham = df[df['class'] == 'ham'].count()['class']
print(f'spam:{num_spam}, ham:{num_ham}, spam/ham={num_spam/num_ham:.3g}')
RANDOM_SEED = 0
# トレーニング・評価データ分割、訓練データを間引き・均質化、テストデータを間引き
X = pd.DataFrame(df['text'])
Y = pd.DataFrame(df['class'])
X_train_str, X_test_str, Y_train_str, Y_test_str = train_test_split(X, Y, train_size=0.7, test_size=0.3, random_state=RANDOM_SEED)
spam_ham_ratio(Y) #選別前
train = pd.concat([X_train_str, Y_train_str] , axis=1)
train_ham = train[train['class']=='ham'].sample(n=250, random_state=RANDOM_SEED)
train_spam = train[train['class']=='spam'].sample(n=250, random_state=RANDOM_SEED)
train_sampled = pd.concat([train_ham, train_spam])
X_train_str = train_sampled['text']
Y_train_str = train_sampled['class']
test = pd.concat([X_test_str, Y_test_str] , axis=1)
test_sampled = test.sample(n=100, random_state=RANDOM_SEED)
X_test_str = test_sampled['text']
Y_test_str = test_sampled['class']
spam_ham_ratio(train_sampled) #選別後の訓練データ
spam_ham_ratio(test_sampled) #選別後のテストデータ
spam:747, ham:4825, spam/ham=0.155 #選別前の全データ
spam:250, ham:250, spam/ham=1 #選別後の訓練データ
spam:13, ham:87, spam/ham=0.149 #選別後のテストデータ
ベクトル化
機械学習で扱えるように文章のベクトル化を行います。ベクトル化の手法はいろいろありますが、今回はシンプルに sklearn.feature_extraction.text.CountVectorizerを用いた、テキストごとの単語の出現回数をカウントする方法を取りました。
vec_count = CountVectorizer(min_df=10) #訓練データ全体で10回以上出現する単語のみを扱う
vec_count.fit(X_train_str)
#抽出した単語の総数
print(f'Unique word counts (dimention): {len(vec_count.vocabulary_)}')
# 訓練データとテストデータをベクトル化
X_train = vec_count.transform(X_train_str).toarray()
X_test = vec_count.transform(X_test_str).toarray()
Unique word counts (dimention): 156
#ラベルを扱いやすい1,0に変換(spam=1, ham=0)
Y_train = np.where(Y_train_str.values=='spam',1,0)
Y_test = np.where(Y_test_str.values=='spam',1,0)
得られたベクトルは156次元(156種類の単語のカウント数からなる要素)あり、このまま量子コンピューターへ持ち込むと2022/5現在では計算が困難なレベルです。ただし、比較的レアな単語を表す要素はほとんどのベクトルで0だったりと情報が詰まっているわけではなく、元の次元が多くても2値分類する用途ではそれほどの次元は不要であることが予想されるため、思い切って2次元のベクトルまで次元削減します。そのほか標準化、正規化も同時に行います。(このあたりの処理はQSVMによるFashionMNIST画像分類を参考にしました。)
def transform(X_train_vec, X_test_vec):
# Standardize
ss = StandardScaler()
X_train_vec = ss.fit_transform(X_train_vec)
X_test_vec = ss.transform(X_test_vec)
# Reduce dimensions
pca = PCA(n_components=2)
X_train_vec = pca.fit_transform(X_train_vec)
X_test_vec = pca.transform(X_test_vec)
# Normalize
mms = MinMaxScaler((-1, 1))
X_train_vec = mms.fit_transform(X_train_vec)
X_test_vec = mms.transform(X_test_vec)
return X_train_vec, X_test_vec
X_train, X_test = transform(X_train, X_test)
これまでの処理で得られた訓練データを可視化すると以下のようになります。赤い点がspam文章、青い点がそうでない文章を表しています。
plt.scatter(X_train.T[0],X_train.T[1], c=Y_train, s=0.1, cmap='bwr')
このデータセットに対してスパッと線を入れて、二つに領域を分けるというのがQSVM/SVMで行われるこれからの処理になります。目で見るとなんとなく大体2つに分けれそうなので、適切なハイパーパラメータ(ここではカーネル)を選択できればうまくいきそうに見えます。
QSVMの実行結果
まずは使用するFeatureMap(量子演算、写像$\phi$に対応)の選択をします。ここでは量子の優位性が議論されているZZFeatureMapとよばれるFeatureMapから作られるカーネルを使用します。
feature_map = ZZFeatureMap(feature_dimension=2, reps=3,
entanglement='linear', data_map_func=None,
insert_barriers=False)
kernel = QuantumKernel(feature_map=feature_map, quantum_instance=Aer.get_backend('statevector_simulator'))
以下のコードで訓練データを入力としたときのカーネルの演算により得られる行列(500x500, 500は訓練データの数)と検証用のデータを含む行列(100x500, 100はテストデータの数, 500は訓練データの数)が生成できます。
ここが量子コンピューター(今回はそのシミュレーター)で実行される部分です。
matrix_train = kernel.evaluate(x_vec=X_train)
matrix_val = kernel.evaluate(x_vec=X_test, y_vec=X_train)
(・・・これで量子コンピューターでの実行終わりです。)
得られたカーネルを用いてフィッティングし、訓練データの正答率を確認してみます。
qsvc = SVC(kernel='precomputed')
qsvc.fit(matrix_train, Y_train)
score = qsvc.score(matrix_val,Y_test)
print(f"Mean accuracy on the given test data: {score}")
Mean accuracy on the given test data: 0.95
正答率は 95% という結果を得ることができました。テストデータは100個だったので95個は正解できたということになります。
SVMとの比較
同じ過程を古典のSVMで行ってみます。カーネルはscikit-learnで用意されているデフォルトのものを適用しています。
for kernel in ["linear", "poly", "rbf", "sigmoid"]:
svc = SVC(kernel=kernel)
svc.fit(X_train, Y_train)
score = svc.score(X_test,Y_test)
print(f"Mean accuracy on the given test data: {score} (kernel={kernel})")
Mean accuracy on the given test data: 0.96 (kernel=linear)
Mean accuracy on the given test data: 0.96 (kernel=poly)
Mean accuracy on the given test data: 0.96 (kernel=rbf)
Mean accuracy on the given test data: 0.26 (kernel=sigmoid)
結果、正答率96%とQSVMより1つだけ多く正解しているようです。そもそもこのデータセットは量子コンピューターを使うほどのものではなかったようですね ![]()
今回の検証では古典の方がわずかに優っていますが、Havlicek et al.(2019)ではQSVMのほうが優位なデータセットがあることが示されてます。
次に2次元ベクトルのデータセットをどのように分割したのかをみてみたいと思います。まずは古典の場合、
def plot_result(X1, X2, binary_map):
fig,ax = plt.subplots(figsize=(6,4))
ax.scatter(X_train.T[0],X_train.T[1], c=Y_train, s=0.1, cmap='bwr')
ax.scatter(X_test.T[0],X_test.T[1], c=Y_test, marker=',', s=5, cmap='bwr')
ax.pcolormesh(X1,X2,binary_map,cmap="coolwarm", alpha=0.2, shading='auto')
plt.show()
x1, x2 = np.linspace(-1,1,40), np.linspace(-1,1,40)
X1, X2 = np.meshgrid(x1, x2)
for kernel in ["linear", "rbf"]:
svc = SVC(kernel=kernel)
svc.fit(X_train, Y_train)
binary_map = svc.predict(np.c_[X1.ravel(), X2.ravel()]).reshape(X1.shape)
plot_result(X1, X2, binary_map)
線形カーネルを選択した場合
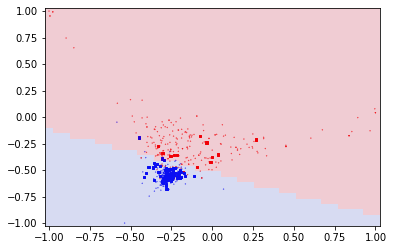
RBFカーネルを選択した場合

それぞれ、選択したカーネルの特徴がでつつ、ざっくり2つの領域に分類しています。
同じことを先ほど試した量子カーネルで行うと、
feature_map = ZZFeatureMap(feature_dimension=2, reps=3,
entanglement='linear', data_map_func=None,
insert_barriers=False)
kernel = QuantumKernel(feature_map=feature_map, quantum_instance=Aer.get_backend('statevector_simulator'))
matrix_train = kernel.evaluate(x_vec=X_train)
matrix_mapping = kernel.evaluate(x_vec=np.c_[X1.ravel(), X2.ravel()], y_vec=X_train)
qsvc = SVC(kernel='precomputed')
qsvc.fit(matrix_train, Y_train)
binary_map = qsvc.predict(matrix_mapping).reshape(X1.shape)
plot_result(X1, X2, binary_map)
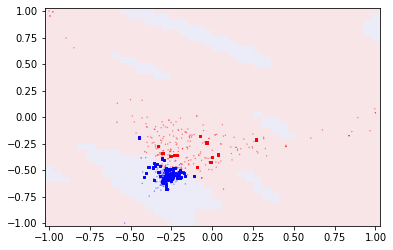
となりました。こちらが今回の領域分割の結果になります。従来のカーネルと比較すると分かるように特になんのデータもないところに孤立した領域がぽつぽつと出てきています。今回の検証では2クラスの領域がまとまっていたため、この何もない領域で境界が現れるのはあまりよろしくないのですが、逆に孤立した領域がたくさん現れるデータセットに対してはこの特徴によってQSVMが有利にはたらくようです。
Havlicek et al.(2019)にて使用されたデータセットによる領域分割結果。論文の図を引用。
まとめ
今回はQiskitのライブラリを用いて、量子コンピューターのシミュレーターでQSVMによる迷惑メール分類を試し、その後通常のSVMとの比較を行いました。


