$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
ユーザーインターフェースを現行版に更新したものをこちらに公開しました。(2021年11月26日追記)
2020年 3/30(月)14:00〜開催のオンラインイベント『中高生向け:量子コンピューター入門 〜長期春休み特別企画〜』のハンズオン資料です。
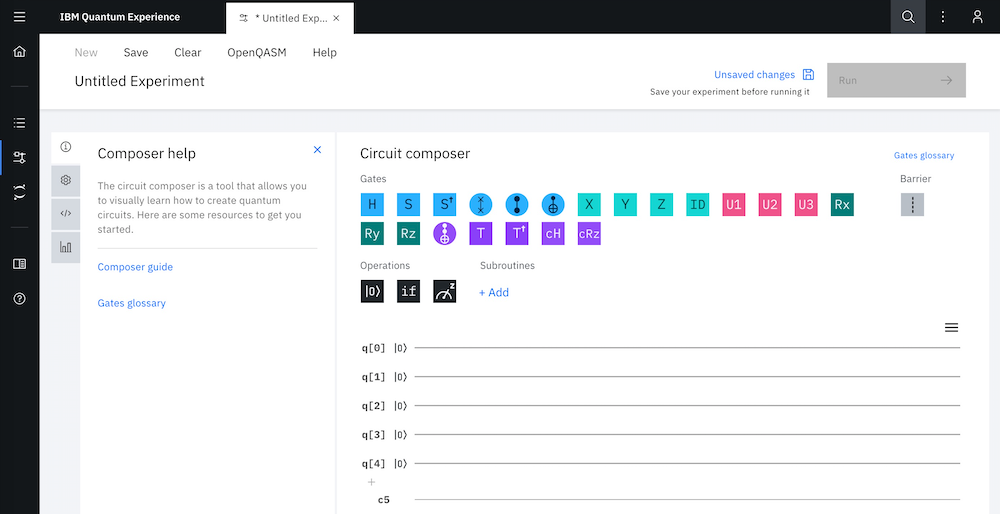
IBM Quantum Experience (https://quantum-computing.ibm.com/) を使って、量子コンピューターの計算をしてみましょう。パソコンまたは、iPadなどのタブレット端末で実行できます。
0. はじめの設定
0-1) ホーム画面からComposer(コンポーザー)画面へ行く
まず、こちらからログインします。ID登録がまだの方は、『IBM Quantum Experienceへの登録(くわしいバージョン)』を参考に、登録してください。
ログインできたら、左側の家マークをクリックして、ホーム画面に行きます。
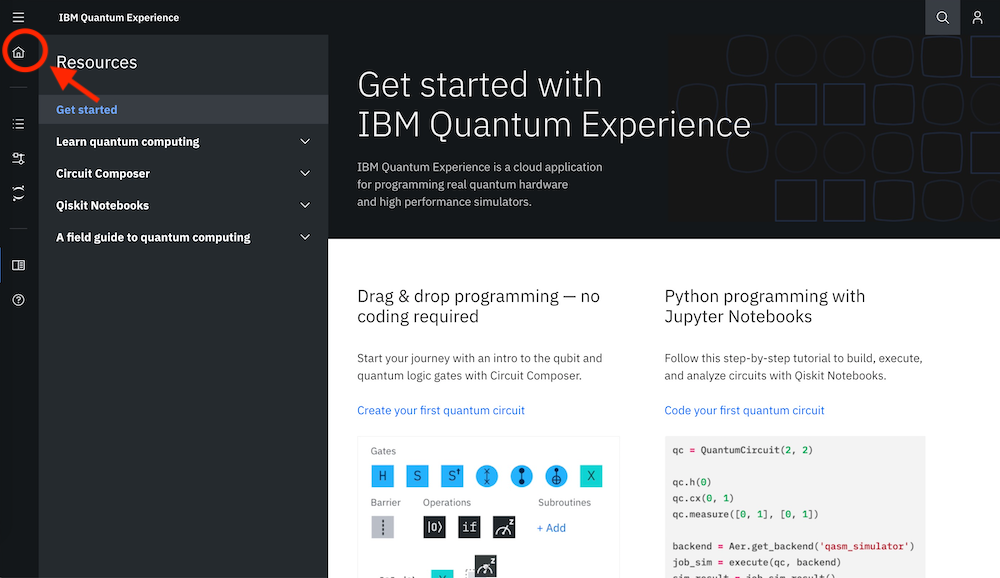
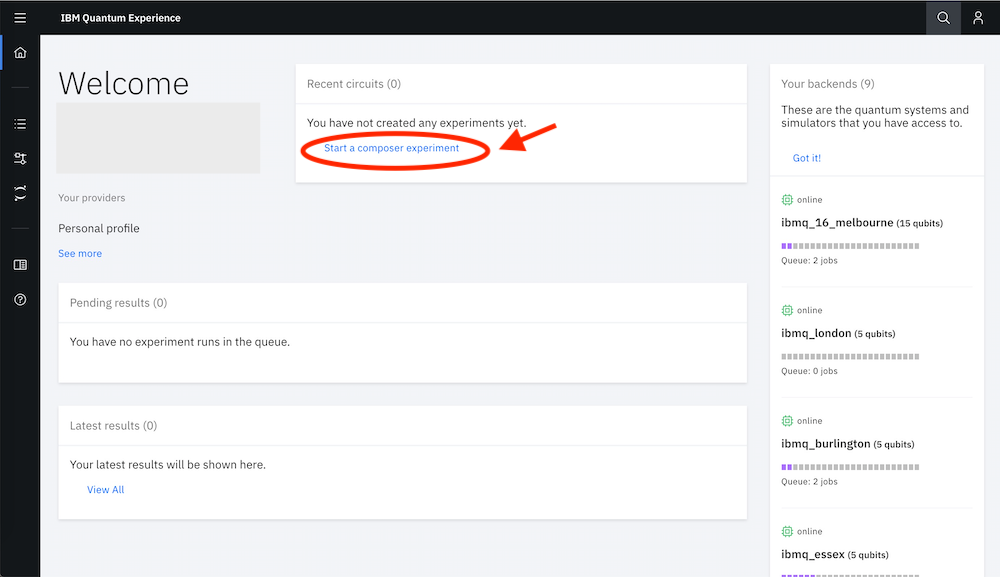
ホーム画面の真ん中の上ぐらいにある青字の「Start a composer experiment」をクリックします。
0-2) 量子ビットの数の設定
初期設定では、5量子ビットが並んでいますが、まず、1量子ビットで実験しますので、1量子ビットの回路に変更します。また、棒グラフで結果を見やすくします。
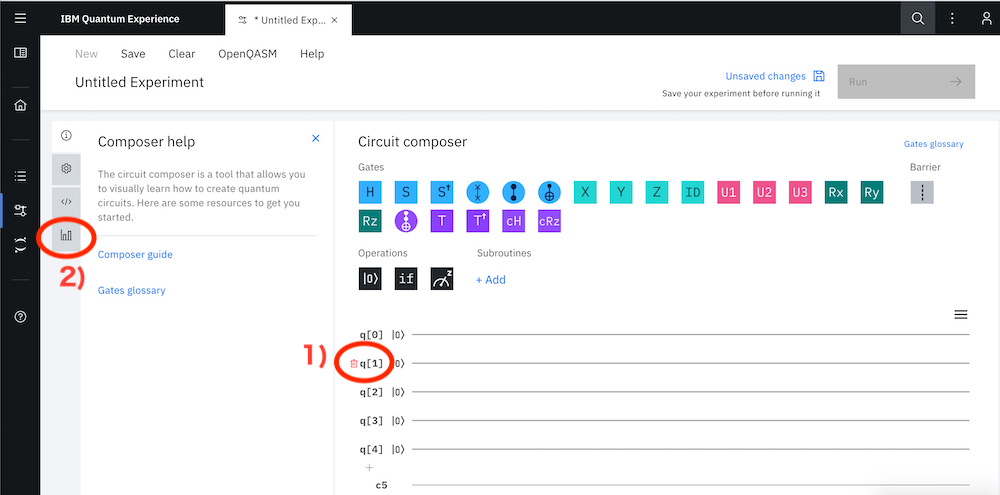
1)マウスをq[1]に近づけると、左側にゴミ箱マークが出てくるので、クリックして消します。同じように繰り返して、q[0]だけ残します。量子ビットが1つだけの回路になりました。
2)左側の棒グラフのアイコンをクリックして、青いグラフを出してください。
下の画面がセットできたら、始めましょう。
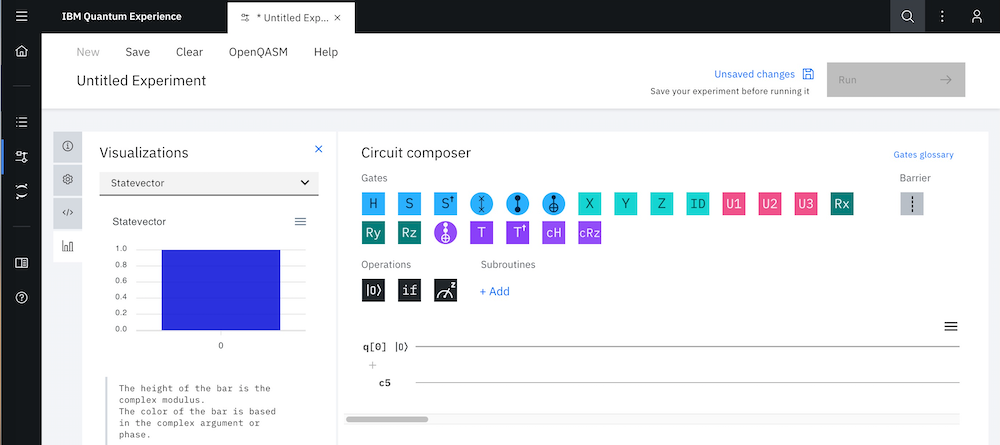
1. Xゲート
右上に並んんでいるH,S,・・・X,Y, などの量子ゲートの箱をドラッグアンドドロップで下の回路に移動させて量子回路を作っていきます。
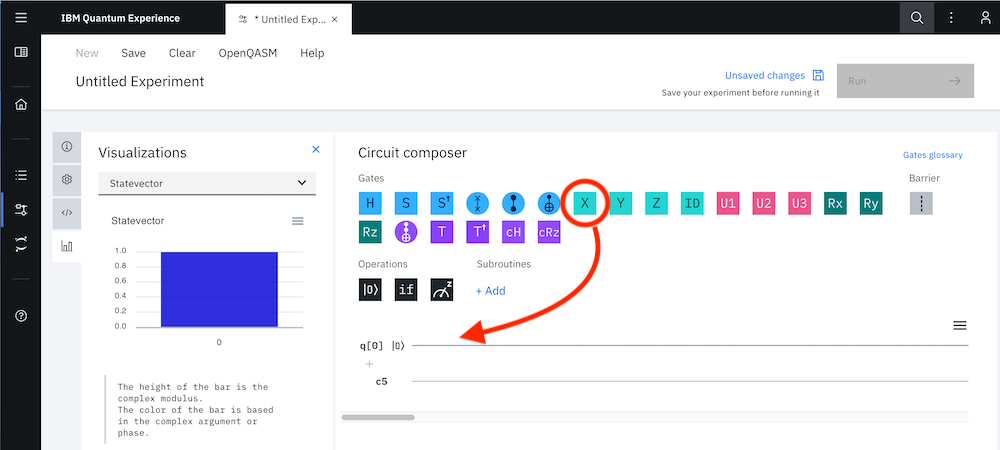
図の回路を作ってみてください。それぞれ左側の棒グラフの変化を確認しましょう。
1-1) 
1-2)
1-3)
量子ビットの初期値は、$\ket{0}$ なので、 反転ゲート のXを1回使うと$\ket{0}$が$\ket{1}$に、また2回使うと$\ket{0}$に戻ることが左側の棒グラフを見て確認できます。
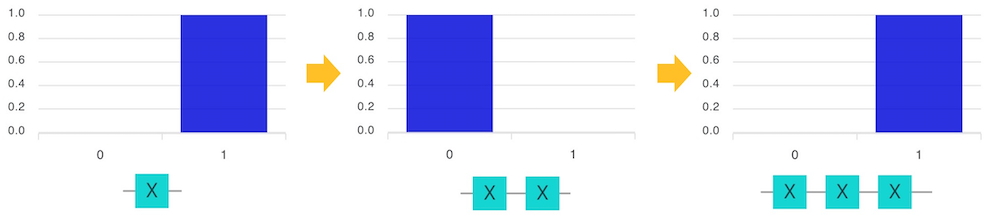
次の章に移る前に、Xゲートをクリックして、右肩のバツマークを出し、バツをクリックしてゲートをクリアしてください。この方法で3つのXゲートを削除して、量子回路をきれいにしてください。

2. Hゲート
Hゲートは、アダマールゲートと呼ばれるもので、量子重ね合わせ状態を作ることができる重要なゲートです。$\ket{0}$が、$\ket{0}$と$\ket{1}$の重ね合わせ状態になります。
次の図の回路を作ってみてください。左側の棒グラフの変化を確認しましょう。
2-1)
量子ビットの初期値は$\ket{0}$ なので、アダマールゲートHを適用すると、$\ket{0}$と$\ket{1}$の重ね合わせ状態になります。これは、$\ket{0}$でもあり$\ket{1}$でもある状態ですが、量子ビットを測定するまでどちらの状態かわかりません。
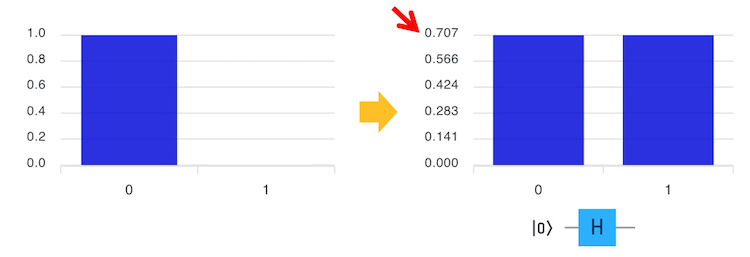
棒グラフのメモリに0.707があるのが読めますが、式で書くと、
$\ket{0} →(H)→ 0.707\ket{0}+0.707\ket{1}$
です。(高校生向け:これは、$\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1}$ と等しいです。)
測定する前にどのくらいの確率で$\ket{0}$と$\ket{1}$が測定されるか事前に予測できます。下の図のように、棒グラフの上の「Statevector(状態ベクトル)」をクリックして「Measurement Probabilities(測定確率)」にしてみましょう。00000と00001の確率が50%ずつの均等な重ね合わせの状態ができていることがわかります。これは、この状態の量子ビットを測定すると0か1のどちらかが観測されるのですが、たくさん測定されると、例えば1000回測定されると約500回は0が観測され、約500回は1が観測されるということです。
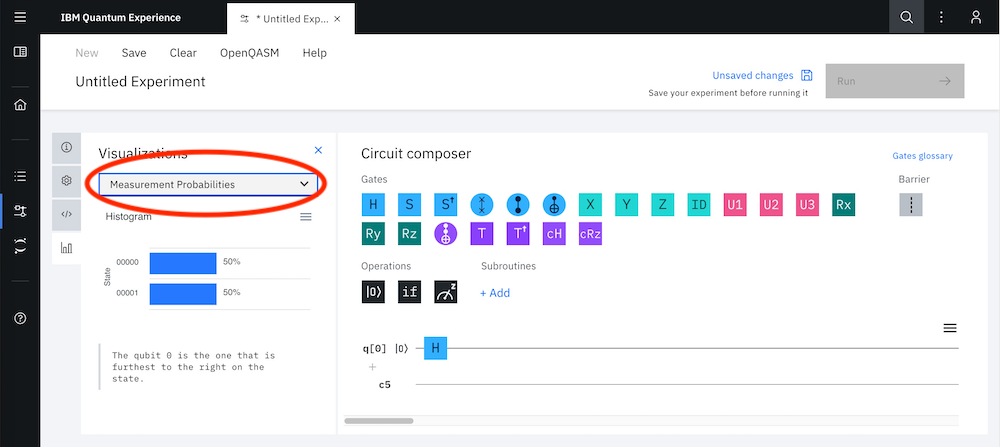
続けます。
2-2) Hゲートも2回繰り返すと棒グラフの値が元に戻ることを確認しましょう。

2-3)
$\ket{0}$にXゲートを使うと$\ket{1}$になり、$\ket{1}$にHゲートを使うと棒グラフの$\ket{1}$の部分が黄色になりました。これはマイナス(ー)の意味があります。
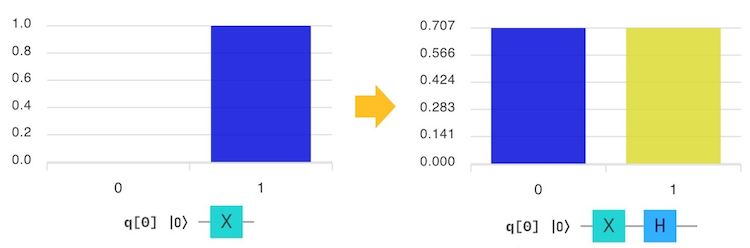
式で書くと、
$\ket{1} →(H)→ 0.707\ket{0}-0.707\ket{1}$
です。(高校生向け:これは、$\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1}$ と等しいです。)
$\ket{0}$にHゲートだけを使った状態と同じように、$\ket{0}$でもあり$\ket{1}$でもある状態ですが、$\ket{1}$の前にマイナス(ー)がついているので、別の状態と考えて計算に使います。
2-4) 続けてHゲートをもう一度かけると棒グラフはどうなりますか?

2-5) q[0]の下にある灰色の「+」マークをクリックして2量子ビットの回路をセットし、Hゲートをそれぞれ使ってみましょう。棒グラフには何個の状態がありますか?

2-6) 5量子ビットの時の重ね合わせです。何通りの状態ができますか?

3. Zゲート
次の図の回路を作ってみてください。それぞれ左側の棒グラフの変化を確認しましょう。
3-1)
3-2)

左側の棒グラフの色は何色になりましたか?
Zゲートは、$\ket{1}$に操作するとマイナスがつくゲートです。
$\ket{0} →(Z)→ \ket{0}$
$\ket{1} →(Z)→ -\ket{1}$
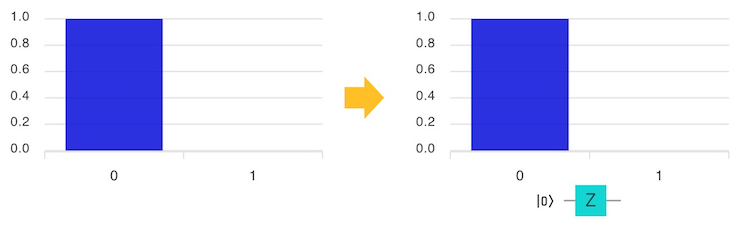
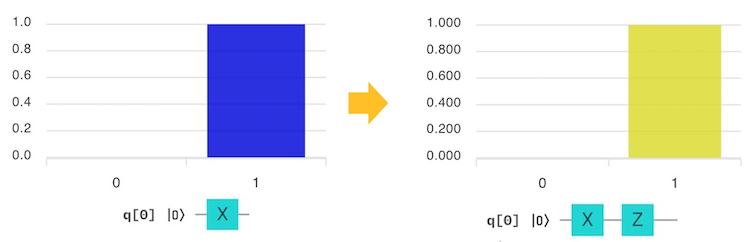
棒グラフの色と下の数字のプラス・マイナスの符号を確認してみましょう。
Zゲートは、重ね合わせの+と-の符号を入れ替えるゲートです。
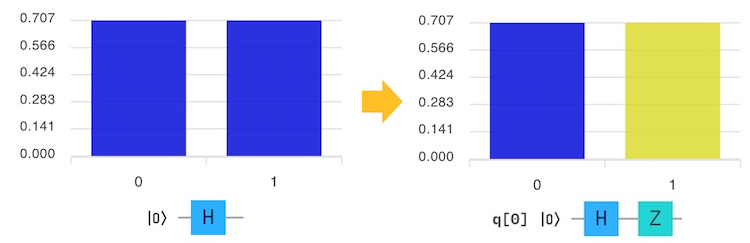
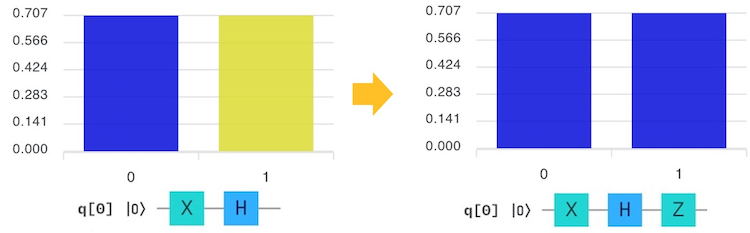
〜〜高校生向けの説明〜〜
Hゲートは$\ket{0}$と$\ket{1}$の重ね合わせを作るゲートでしたので、
$\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1} → (Z) → \frac{1} {\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1} $
$\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1} → (Z) → \frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1} $
になっていることが確認できると思います。このとき
$\frac{1}{\sqrt{2}}\ket{0}+\frac{1}{\sqrt{2}}\ket{1} =\ket{+}$
$\frac{1}{\sqrt{2}}\ket{0}-\frac{1}{\sqrt{2}}\ket{1} =\ket{-}$
とかくことにすると、
$\ket{+} → (Z) → \ket{-}$
$\ket{-} → (Z) → \ket{+}$
になります。
Zゲートは、重ね合わせの+と-の符号を入れ替えるゲートです。
〜〜高校生向けの説明ここまで〜〜
4. 練習問題 A
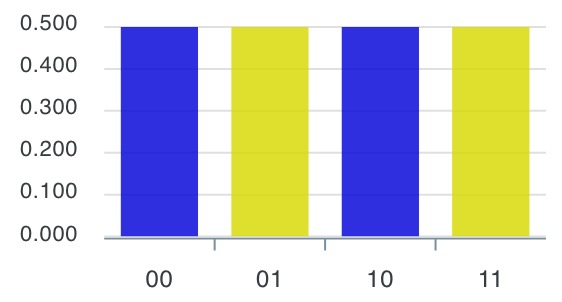
次の棒グラフが表示されるような量子回路を作ってみましょう。答えは一つではないので、どんな作り方でもOKです。
ヒント:棒グラフ下の右側の数字が上側の量子ビットq[0]に対応していることに注目して作ってみましょう。
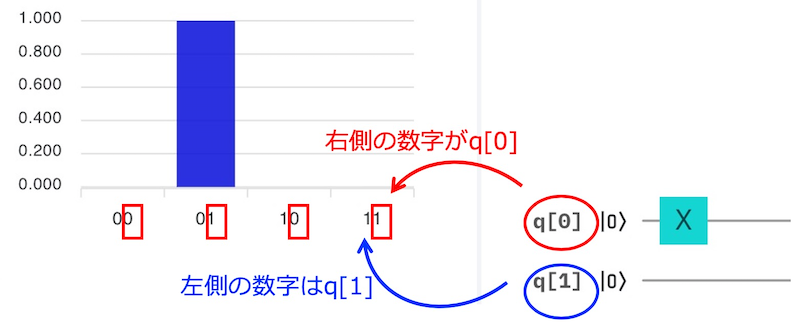
さらにヒント:使うゲートはX、H、Zだけです!
4-1)
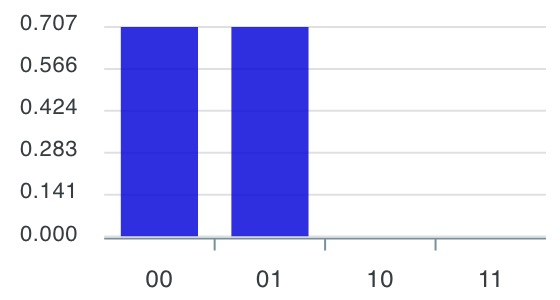
4-2)

4-3)
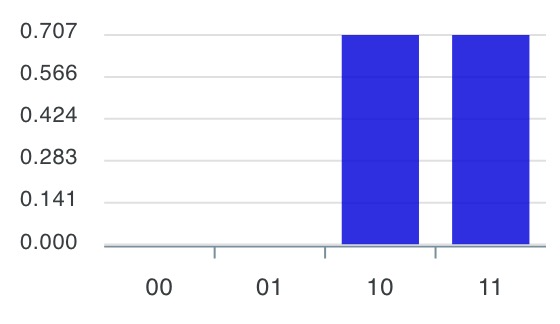
4-4)
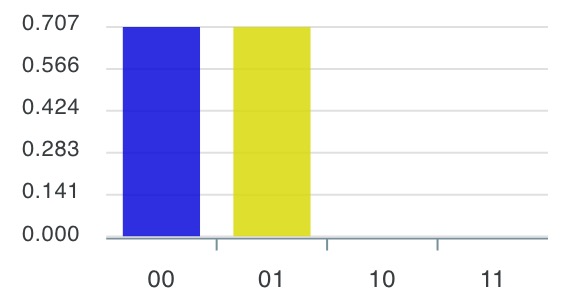
4-5)
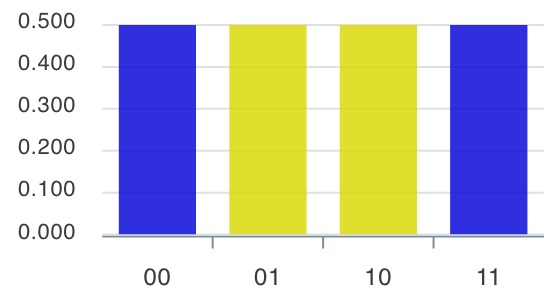
4-6)
次はCXゲートを練習します。
5. CXゲート
CXゲート(コントロールNOTゲート)は2量子ビットを使う計算をします。
CXゲートは、下の図にあるような記号で、+がついていない側が制御ゲート、+がついている側が目標ゲートと呼ばれます。制御ゲートが$\ket{1}$のときのみ、目標ゲートを反転(NOT)するゲートです。下の図では、q[0]がXゲートで$\ket{1}$になっているので、q[1]の値$\ket{0}$を反転して$\ket{1}$にします。
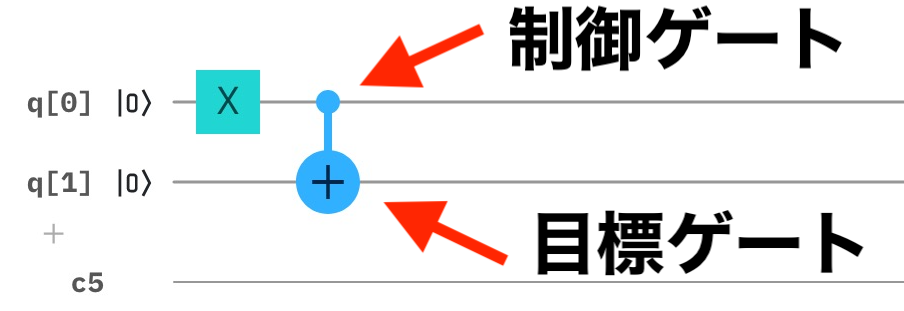
次の図の回路を作ってみてください。q[0]が$\ket{1}$のときのみ、q[1]の値が反転していることを確認しましょう。
5-1)
5-2)
5-3)
5-4)
5-5)
最後の回路の棒グラフを見てみましょう。
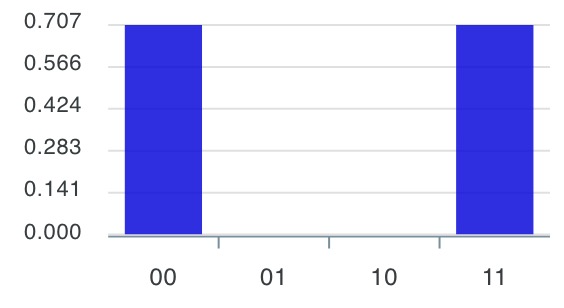
これは、q[0]だけみると$\ket{0}$と$\ket{1}$の重ね合わせ、q[1]だけみても$\ket{0}$と$\ket{1}$の重ね合わせですが、$\ket{00}$, $\ket{01}$, $\ket{10}$, $\ket{11}$の4状態ではなく、$\ket{00}$, $\ket{11}$の2つの状態のみになっています。
これはエンタングルメント状態とよばれる量子状態で、q[0]が$\ket{0}$のときはq[1]も$\ket{0}$、q[0]が$\ket{1}$のときはq[1]も$\ket{1}$という、q[0]とq[1]が切っても切れない関係になっている特別な状態です。量子コンピューターはこのエンタングルメント状態を上手に使って複雑な計算を行っていきます。
このエンタングルメント状態の2つの量子ビットを遠くに離した時、例えば、片方は地球上に置いたまま、もう片方は宇宙の遥か遠くに離した時を考えます。それぞれ$\ket{0}$と$\ket{1}$の50%ずつの重ね合わせ状態でどちららか分からないのですが、地球の量子ビットを測定してそれが$\ket{0}$だと判明すると、遠くの宇宙にある量子ビットも$\ket{0}$だと瞬時にわかるという不思議な現象が起こることが考えられます。この思考実験は、アインシュタインが考えたもので、アインシュタインはこれを不気味な遠隔作用と呼び、疑っていたのですが、このエンタングルメント状態は今、IBMの量子コンピューターで誰でも実験してみることができます。

これまでは、IBM Quantum Experienceの計算機能のみ使っていたので、実際に測定してみましょう。
6. 測定してみる
次のようにして測定します。
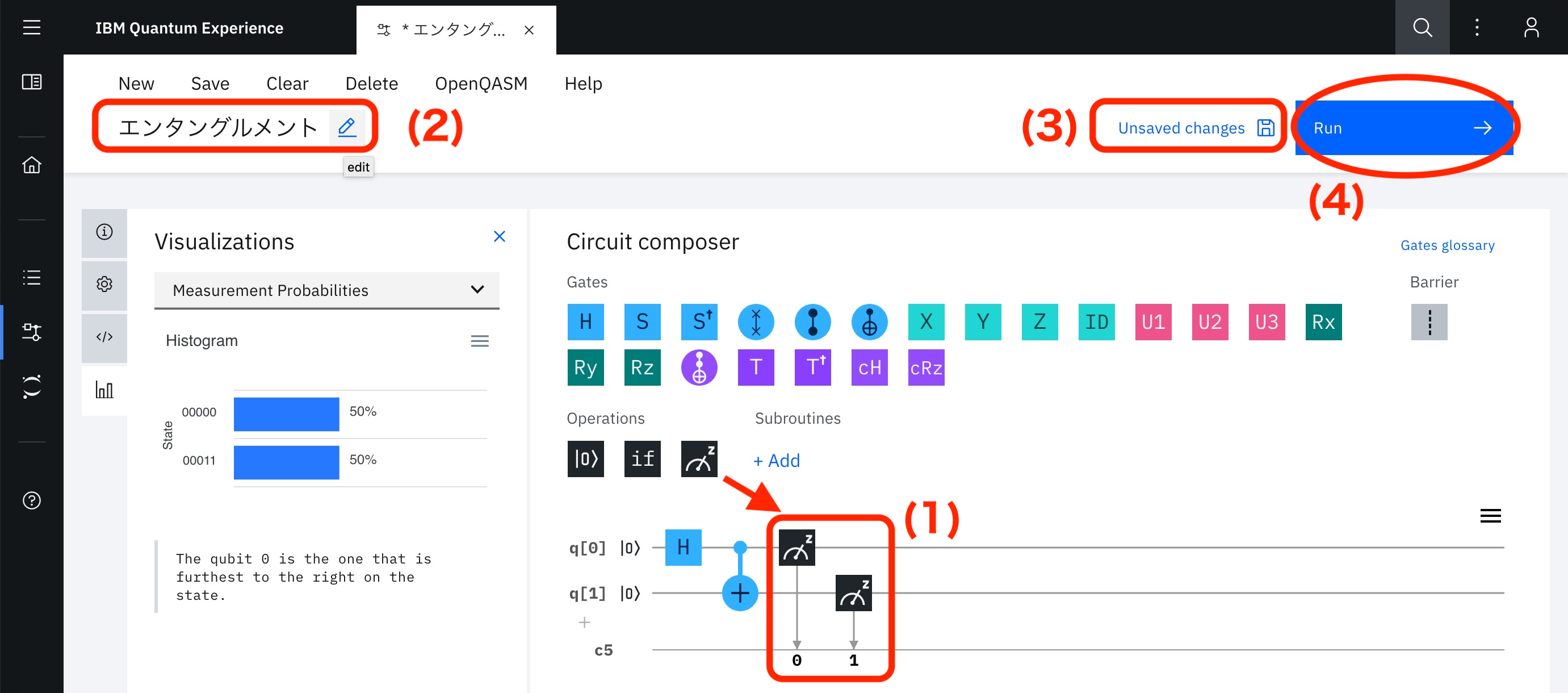
(1) 測定ゲートをq[0]とq[1]に設置します。
(2) 左上の「Untitled Experiment(名無しの実験)」あたりにマウスを持っていくと鉛筆マークが出てくるのでクリックして名前を「エンタングルメント」などにします。
(3) 右上の「Unsaved changes(未保存の変更あり)」をクリックして保存します。
(4) その横の「Run(実行)」をクリックします。
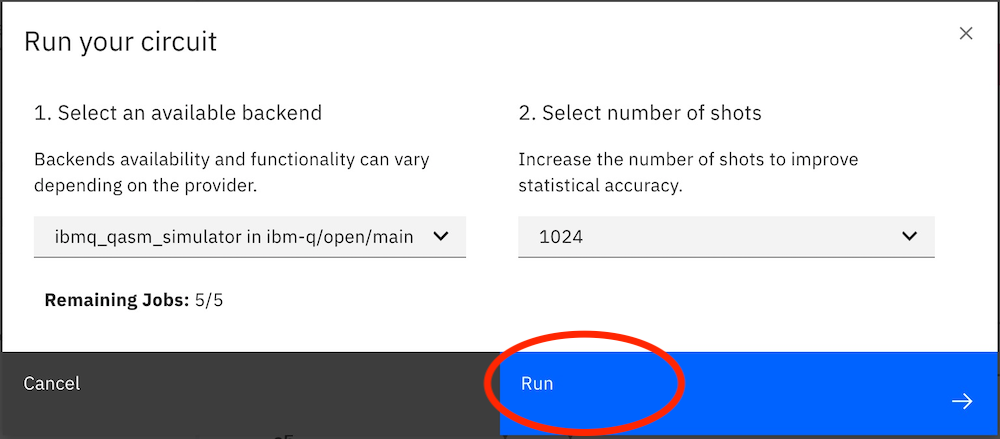
(5) 下の図のようなウィンドウが出てきます。
まず、量子シミュレーターでやってみましょう。シミュレーターは、本物の量子コンピューターで実験する前に、普通のコンピューターで計算してみて回路があっているか確認するために使います。初期設定ではシミュレーターになっているので、このまま「Run(実行)」をクリックします。
(6) 画面下の方に「Results(結果)」と出たら青字の結果をクリックします。
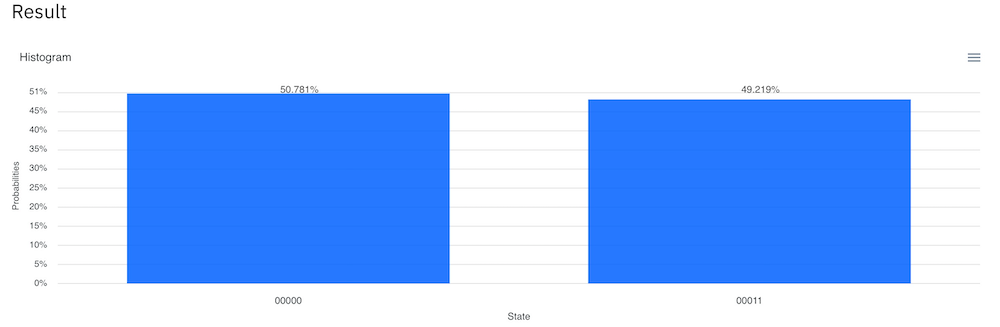
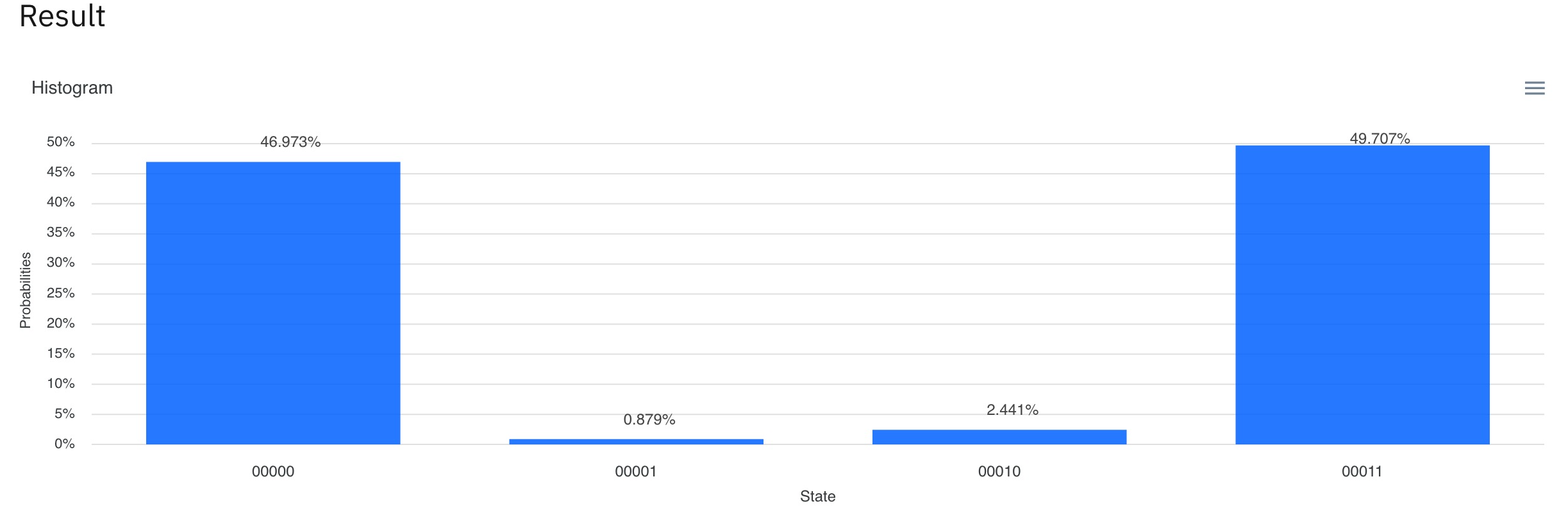
(7) 結果を見てみましょう。00000が約50%、00011が約50%ずつ観測されたことがわかります。より50%に近くするにはショット数を大きくします。
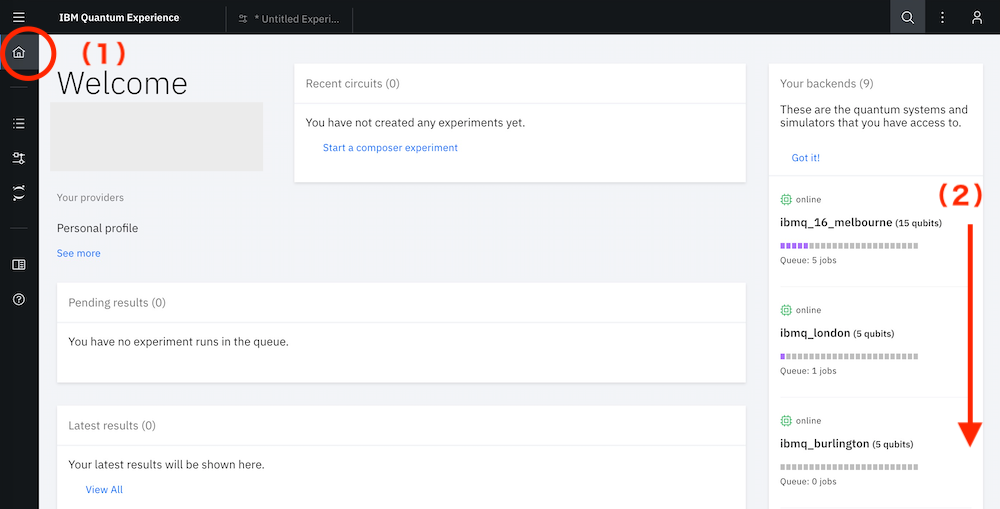
次に、ニューヨークにあるIBMの実物の量子コンピューターでやってみましょう。
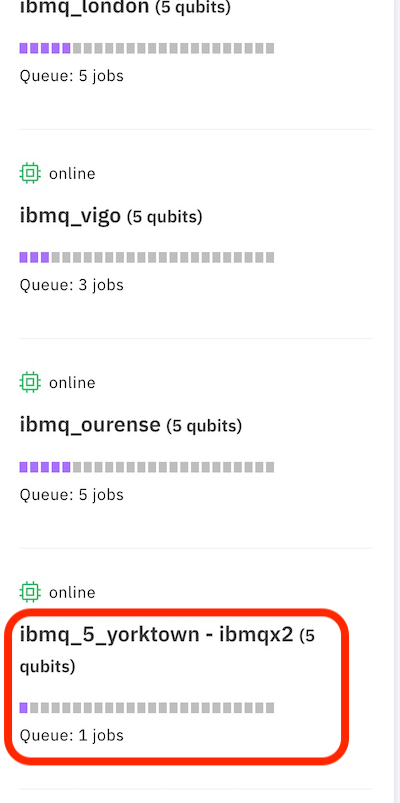
左側の(1)家アイコンをクリックしてホーム画面に戻り、(2)のようにスクロールして一番空いている(Queueの少ない・紫のバーが短い)量子コンピューター・デバイスを見つけて覚えておきます。(下から2番目の「ibmq_armonk」は1量子ビットなので選ばないでください。一番下はシミュレーターなのでこれも除きます。)IBMの量子コンピューターは、世界中の人が実験しているため、多少混んでいるときがあります。
私が今、この文書を書いている時には、「ibmq_5_yorktown - ibmqx2 (5 qubits)」が1個のみ実験を待っている状態で最も空いていましたので、この名前をメモしました。
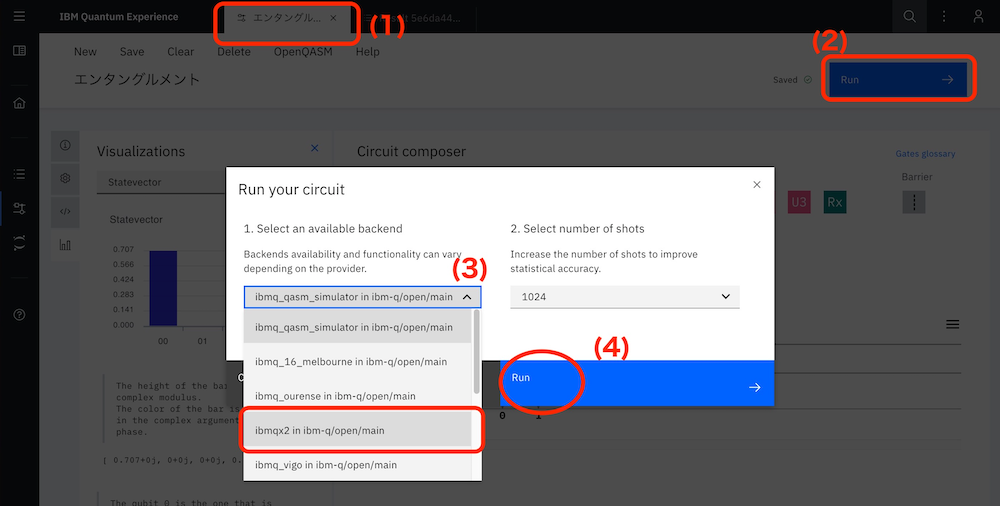
(1)量子回路のタブに戻り、(2)「Run(実行)」をクリックし、(3)メモした実物の量子コンピューター名を探し、選択します。(4)「Run」で実行します。
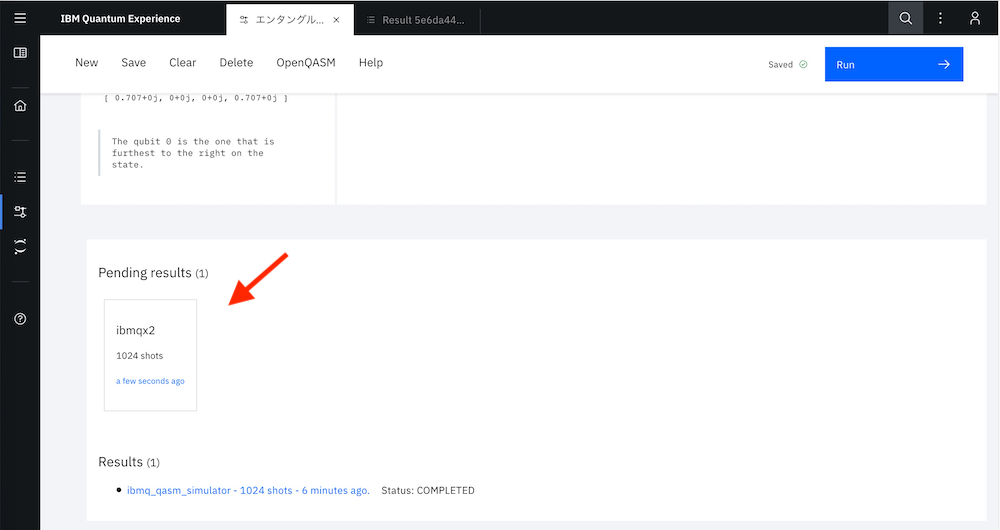
混雑の具合にもよりますが、しばらく、下の図のように結果待ちになります。
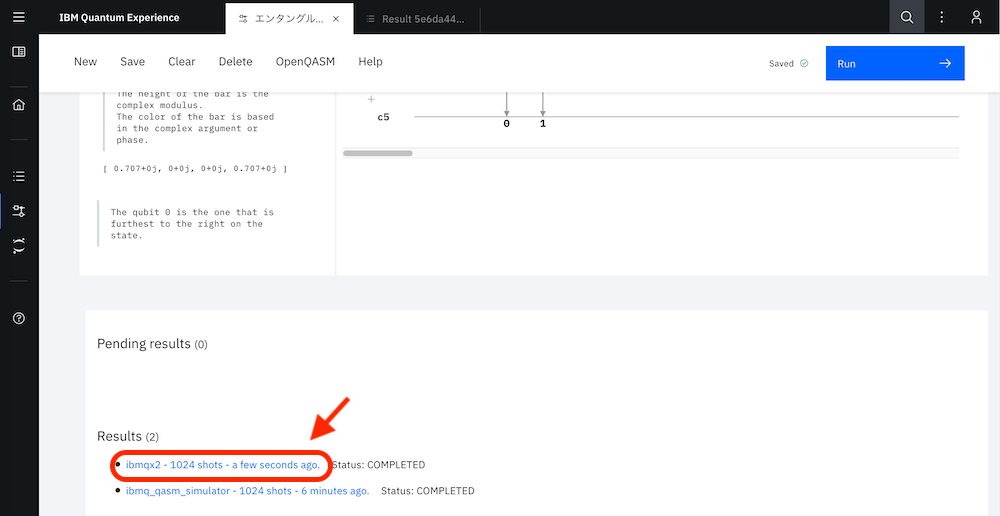
下のように「Pending results(保留中の結果)」がなくなり「Results(結果)」に移ったら、結果をクリックしてみてみましょう。
シミュレーションの時とちがって、000000と00011以外の結果、00001、00010も出ています。実際の量子コンピューターはまだ完璧ではなく、このように結果にエラーが含まれますが、00000と00011が最も多く観測されることがわかります。
7. 練習問題 B
次の状態の量子回路を作ってみましょう。答えは一つではないので、どんな作り方でもOKです。
ヒント:使うゲートはX、H、Z、CXゲートだけです!
7-1) $\frac{1}{\sqrt{2}}(\ket{00}-\ket{11})$

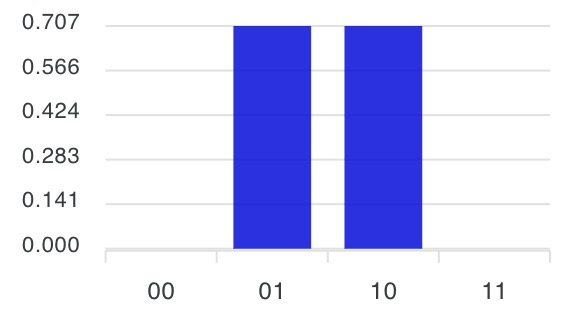
7-2) $\frac{1}{\sqrt{2}}(\ket{01}+\ket{10})$
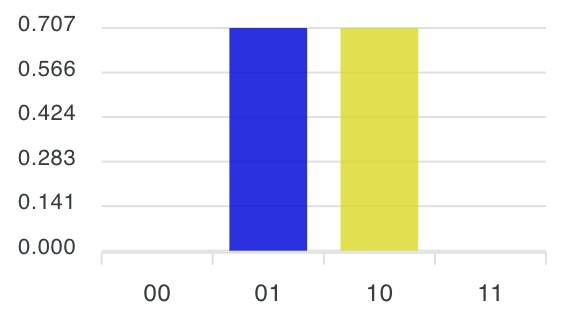
7-3) $\frac{1}{\sqrt{2}}(\ket{01}-\ket{10})$
みなさん、最後までできましたか?
ぜひ感想を下のコメント欄に残してください。
更新履歴
2020/04/17:ユーザーインターフェースUpdateによる画面操作方法の更新。