$$
\def\bra#1{\mathinner{\left\langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$
今年、会社の勉強会で量子フーリエ変換のところを担当した際に、IBM Q Experience や Qiskit で書かれている基本的な量子フーリエ変換のコードがあまり見つからなかったので、まとめておきたいと思います。一般的な量子コンピューターの教科書と Qiskit は、ビット配列の向きが逆なので、教科書でアルゴリズムの勉強をした後に、Qiskit でコーディングする際には、少し注意が必要になります。(このまとめではアルゴリズムの導出は省略します。)
フーリエ変換
フーリエ変換とは、関数を三角関数(サイン・コサイン)の足し算に変換することです。(Wikipediaのフーリエ変換のページには動画がついていて分かりやすいです。)
例えば、下の関数は、3つのsin波の足し算でできていますが、そのsin波の振動数ごとの和に変換する作業がフーリエ変換です。

周期性を持った波をフーリエ変換するとその周波数と振幅が出力されます。逆フーリエ変換は逆の作業(周波数と振幅を入力すると、その周期を持った波が出力される)になります。(周期性を持っていない関数でもフーリエ変換はできます。)

量子フーリエ変換
一方、量子フーリエ変換は、周期の値を入力すると、位相にその周期の値の周期性を持った量子状態が出力されます。前述の量子ではない方のフーリエ変換とは意味合い的に逆で、量子フーリエ変換は、量子でない方の逆フーリエ変換に相当します(量子だから逆なのではなく、離散的フーリエ変換になると名前が逆になるそうです)。
逆量子フーリエ変換の方は、量子状態の位相の周期を見つけることができ、ショアのアルゴリズム(素因数分解のアルゴリズムの一部)に使われています。
下の図はイメージです。
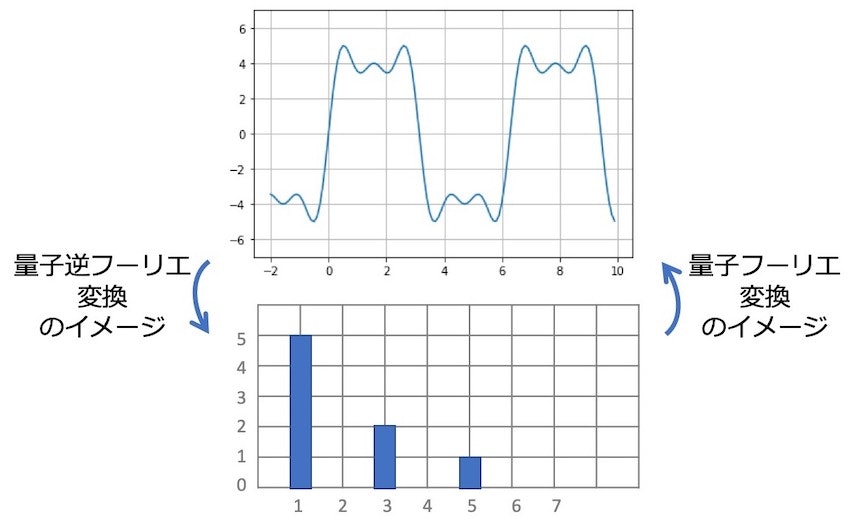
例えば、3量子ビットで$\ket{001}$を量子フーリエ変換すると、$\ket{000}$から$\ket{111}$まで8個の量子状態が均等な重ね合わせで、それぞれの波の位相が周期1で少しずつ変化している状態が出力されます。同様に、$\ket{010}$を量子フーリエ変換すると、$\ket{000}$から$\ket{111}$まで8個の量子状態の位相が周期2で少しずつ変化している状態が出力されます。
さっそく IBM Q Experience (https://quantum-computing.ibm.com/) でやってみます(アルゴリズムの導出は教科書でご確認ください)。 IBM Q Experience の State vector(状態ベクトル)表示は、位相の値によってグラフの色が変化するため周期性が一目でわかります。
3量子ビットの例
$\ket{001}$ を下の図の量子回路で量子フーリエ変換すると、状態ベクトルは下の図の棒グラフのように変化します。現時点での最新版のIBM Q Experienceには、制御回転ゲートであるcU1ゲートのアイコンがなくなってしまっていますが、QASMで書くと出てきます。(QASMコード例:cu1(pi/2) q[1],q[2]; など)

棒グラフの下の[ ]内の数値は各状態の係数で、量子フーリエ変換(QFT)で以下のように変化することが示されています。係数の絶対値の二乗はその状態が観測される確率になりますが、今回は8個の状態の均等な重ね合わせなので、1/8 (= $|\frac{1}{\sqrt{8}}|^2 = |0.354|^2 $ )ずつの確率になります。
$\ket{001} \rightarrow (QFT) \rightarrow $
$
\frac{1}{\sqrt{8}}\ket{000}
- (\frac{1}{\sqrt{16}} +\frac{i}{\sqrt{16}})\ket{001}
- \frac{1}{\sqrt{8}}i\ket{010}
- (-\frac{1}{\sqrt{16}}+\frac{i}{\sqrt{16}})\ket{011}$
$- \frac{1}{\sqrt{8}}\ket{100}
-(\frac{1}{\sqrt{16}} +\frac{i}{\sqrt{16}})\ket{101}
-\frac{i}{\sqrt{8}}\ket{110}
+(\frac{1}{\sqrt{16}} -\frac{i}{\sqrt{16}})\ket{111}$
この係数つまり、各量子状態の位相が下のグラフ(Q Experienceからではなく私の自作)のように複素数空間で反時計回りに少しずつ変化し、$\ket{000}$から$\ket{111}$の間で周期1で変化します。IBM Q Experienceの状態ベクトルの棒グラフは位相ごとに色が異なり、分かりやすいですが、虚数部に関しては正と負が同じ色になっているようです。

$\ket{010}$ を量子フーリエ変換すると、状態ベクトルは下の図の棒グラフのように変化します。これは周期2です。

この時の位相は以下の4つの値を2周します。

同じく$\ket{011}$ の量子フーリエ変換は周期3です。

この時の位相のベクトルは以下のように135度ずつ回転し、3周します。

4量子ビットの例
4量子ビットの量子フーリエ変換の回路はIBM Q Experienceでは以下のようになります。

この回路に、例えば、$\ket{0001}$ 、$\ket{0010}$ 、$\ket{0011}$ をそれぞれ入力すると、以下のように$\ket{0000}$から$\ket{1111}$まで16個の量子状態の位相がそれぞれ周期1、2、3で少しずつ変化する状態ベクトルが出力されます。

5量子ビットの例
5量子ビットの量子フーリエ変換の回路はIBM Q Experienceでは以下のようになります。

この回路に、例として、$\ket{00001}$ 、$\ket{00100}$ 、$\ket{10000}$ をそれぞれ入力すると、以下のように$\ket{00000}$から$\ket{11111}$まで32個の量子状態の位相がそれぞれ周期1、4、16で変化する状態ベクトルが出力されます。

Qiskitで量子フーリエ変換
Qiskitで3量子ビットの量子フーリエ変換を書いてみます。
import math
from qiskit import Aer, IBMQ
from qiskit import QuantumRegister, ClassicalRegister, QuantumCircuit, execute
q = QuantumRegister(3)
c = ClassicalRegister(3)
qft3 = QuantumCircuit(q, c)
qft3.h(q[2])
qft3.cu1(math.pi/2.0, q[1], q[2])
qft3.cu1(math.pi/4.0, q[0], q[2])
qft3.h(q[1])
qft3.cu1(math.pi/2.0, q[0], q[1])
qft3.h(q[0])
qft3.swap(q[0],q[2])
qft3.draw(output='mpl')
$\ket{000}$を量子フーリエ変換すると位相が全て同じ状態の$\ket{000}$から$\ket{111}$の均等な重ね合わせが出力されます。
statevector_simulatorを使った結果は、以下のようになり、全て同じ位相であることが確認できます。
backend = Aer.get_backend('statevector_simulator')
job_sim = execute(qft3, backend)
sim_result = job_sim.result().get_statevector()
print(sim_result)
[0.35355339+0.j 0.35355339+0.j 0.35355339+0.j 0.35355339+0.j
0.35355339+0.j 0.35355339+0.j 0.35355339+0.j 0.35355339+0.j]
以下はシミュレーションと実機で計算した結果です。
for i in range(3):
qft3.measure(q[i],c[i])
# シミュレーターで実行
backend = Aer.get_backend('qasm_simulator')
simulate = execute(qft3, backend=backend, shots=1024).result()
simulate.get_counts()
plot_histogram(simulate.get_counts())
# 実機で実行
from qiskit.tools.monitor import job_monitor
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmqx2')
shots = 2048
job_exp = execute(qft3, backend=backend, shots=shots)
job_monitor(job_exp)
from qiskit.tools.visualization import plot_histogram
results = job_exp.result()
plot_histogram([simulate.get_counts(),results.get_counts()], legend=['qasm_simulator','ibmqx2'])
逆量子フーリエ変換
逆量子フーリエ変換は、量子フーリエ変換の逆で、位相に周期性のある量子状態を入力すると、その周期を出力します。例えば5量子ビットの逆量子フーリエ変換の回路はIBM Q Experienceでは、以下のようになります。

例として、周期1と周期8の量子状態を以下ようにZ回転ゲートで作り入力してみると、確かに結果は$\ket{00001}$と$\ket{01000}$のみが得られました。


Qiskitで3量子ビットを用いて、周期1の量子状態を逆量子フーリエ変換してみます。
q = QuantumRegister(3)
c = ClassicalRegister(3)
iqft3 = QuantumCircuit(q, c)
# 周期1の量子状態を作る
for j in range(3):
iqft3.h(q[j])
iqft3.u1(math.pi/float(2**(2-j)), q[j])
iqft3.barrier()
# 逆量子フーリエ変換する
iqft3.swap(q[0],q[2])
iqft3.h(q[0])
iqft3.cu1(-math.pi/2.0, q[0], q[1])
iqft3.h(q[1])
iqft3.cu1(-math.pi/4.0, q[0], q[2])
iqft3.cu1(-math.pi/2.0, q[1], q[2])
iqft3.h(q[2])
iqft3.draw(output='mpl')
シミュレーションと実機で計算してみた結果です。
for i in range(3):
iqft3.measure(q[i],c[i])
# シミュレーターで実行
backend = Aer.get_backend('qasm_simulator')
simulate = execute(iqft3, backend=backend, shots=1024).result()
simulate.get_counts()
plot_histogram(simulate.get_counts())
# 実機で実行
from qiskit.tools.monitor import job_monitor
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmqx2')
shots = 2048
job_exp = execute(iqft3, backend=backend, shots=shots)
job_monitor(job_exp)
from qiskit.tools.visualization import plot_histogram
results = job_exp.result()
plot_histogram([simulate.get_counts(),results.get_counts()], legend=['qasm_simulator','ibmqx2'])
以上、量子フーリエ変換と逆量子フーリエ変換についてIBM Q ExperienceとQiskitでやってみた結果をまとめました。
参考文献
- Qiskit Textbook 3.5 Quantum Fourier Transform (https://qiskit.org/textbook/ch-algorithms/quantum-fourier-transform.html)
更新履歴
2019/12/27 初版
2019/12/29 タイプミス修正
2020/01/08 $\ket{011}$ の量子フーリエ変換の部分の回転角度の数字修正



