井手さんの「異常検知と変化検知」の要点をまとめたもの。
Chapter1
ラベルありデータの場合
ネイマン・ピアソン決定則
観測データを$\boldsymbol x$、異常・正常を示す二値のラベルを$y$として、条件付き確率の比(密度比、尤度比)が閾値を超えた場合に異常($y=1$)と判定する。
$$a(\boldsymbol x') = \ln \frac{p(\boldsymbol{x'} \mid y=1, D)}{p(\boldsymbol{x'} \mid y=0, D)}$$
ラベルなしデータの場合
まず、学習でデータ内に異常データが含まれていない、またはごく少数しか含まれていないとの仮定が必要。
何らかの手法で、$\boldsymbol x$の確率分布$p(\boldsymbol x \mid D)$が求まったとする。
下式の負の対数尤度(情報量)を異常度とする。珍しい観測値が得られるほど、異常度が大きくなることに対応している。
$$a(\boldsymbol x') = -\ln p(\boldsymbol x' \mid D)$$
評価指標
異常検知はほとんどの場合不均衡データを取り扱う。そのため、Precision, Recallではなく、F値やAUCを用いるのが好ましい。
Chapter2 ホテリングのT^2法
各標本が独立に多変量正規分布に従うと仮定する。
データから推定した平均、共分散行列(それぞれ、$\hat{\mu}, \hat{\Sigma}$)を用いて、下記のマハラノビス距離により異常度を定義。観測データの平均からのどの程度離れているかを表す。上図では異常度を色で表現している。
$$a(x')=(x' - \hat{\mu})^\mathsf{T} \hat{\Sigma}^{-1} (x' - \hat{\mu})$$
ここで、標本数$N$がデータの次元$M$より十分大きい場合、$a(x')$は自由度$M$の$\chi^2$分布に従うことを利用して、所定の誤報率に基づいて異常度の閾値を設定できる。
Chapter3 単純ベイズ法
ナイーブベイズ法では、データの各次元が独立と考え、パラメータ推定を行う。変数間に相関がある場合はうまくいかない。
二値分類において一般的に使われるベイズ決定則(下式)は誤り確率を最小にする判別規則だが、異常検知の場合$p(y=1)\ll p(y=0)$であるため、異常判定が強く抑制される。判定の閾値を適切に調整する必要がある。
$$\ln \frac{p(y=1 \mid x)}{p(y=0 \mid x)} = \frac{p(x \mid y=1)p(y=1)}{p(x \mid y=0)p(y=0)}>0 \ \Leftrightarrow \ y=1 $$
Chapter4 近傍法
ホテリング法のように、データが多変量正規分布に従うとの仮定が適切でない場合(例えば分布が多峰の場合)にも適用可能な方法。
Local outlier factor (局所外れ値度)、マージン最大化近傍法などがある。
Chapter5 混合分布モデル
データに対して混合分布モデルをフィッティングした上で、新規データに対する負の対数尤度を算出、異常度として用いる。パラメータ推定にはEMアルゴリズムなどを用いる。
単一の多変量正規分布に限られたホテリング法の欠点を改良した手法の1つ。
Chapter6 サポートベクトルデータ
更新予定。
Chapter10 疎構造学習
ホテリングの$T^2$法などは、平均値が変化しない量の監視に用いられる。変数間に一定の関係を保ちつつも、値自体が変化するデータの場合、変数間の関係に着目した異常検知が考えられる。
変数の関係をグラフで表現ですることを考える。
pairwise Markov graph
2変数の間の関係にのみ注目する単純なモデル。
「(他の変数で条件付けると)2変数が独立」$\Leftrightarrow$「2つのノードを結ぶエッジがない」、としてグラフを構築する。
Gaussian graphical model
確率分布として多変量正規分布を想定したマルコフグラフモデル。
pairwise Markov graphの場合、各成分を標準化したもとで、
**「精度行列$\Delta$の$(i, j)$成分$\Delta_{i,j}=0$」$\Leftrightarrow$「$x_i, x_j$が独立」 **となる。
graphical LASSO
多変量正規分布の精度行列を求めれば、変数間の相関構造を知ることができる。
その際、本質的な直接相関を捉えたなるべく疎な(スパースな)精度行列を求めることが好ましい。
Graphical Lassoは多次元正規分布の精度行列をスパース推定する方法。
精度行列の事前分布としてラプラス分布を設定した上で、MAP推定により精度行列を推定すると、
$$\Delta^* = \rm{argmax}_\Delta (\ln det \Delta - \rm{tr}(S \Delta) - \rho ||\Delta || _1)$$
となることが分かる。ここで、$||\Delta || _1$は$\Delta$の非対角成分の絶対値の和である。
第3項はいわゆるL1正則化の形になっていることが分かる。正則化パラメータ$\rho$は交差検証によって決定する。
下図は正則化パラメータを大きくするにつれて、推定されるグラフ構造が変化していく様子を表している。
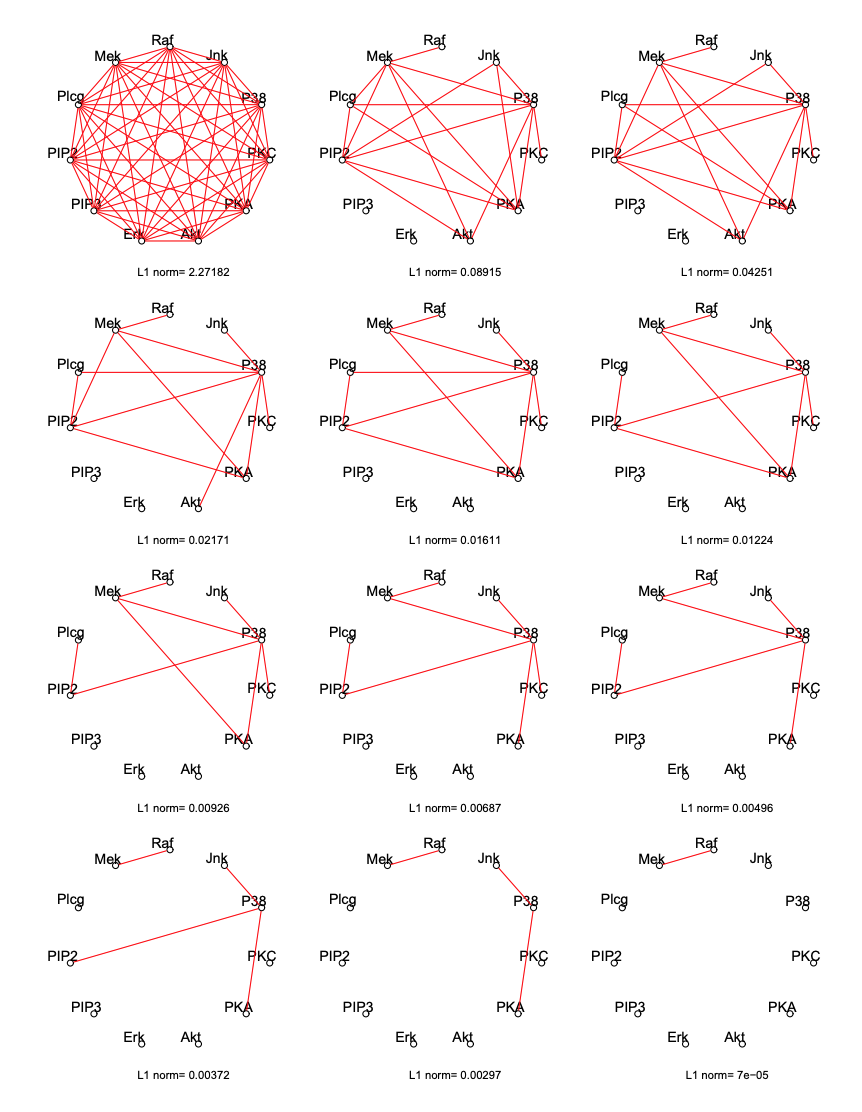
出典:http://statweb.stanford.edu/~tibs/sta306bfiles/graph_main.pdf
Pythonでの実装例は、scikit-learnのドキュメントを参照。概要は以下の通り。
スパースな共分散行列をもつ多変量正規分布から、比較的少ないサンプルを取得し、普通に標本共分散行列を求めてもスパースとはならない。ところがGraphical Lassoを用いることで、真の共分散行列に近いスパースな行列が推定できることが分かる。
異常度の計算
Graphical Lassoによる精度行列推定の結果を用いた異常検知の方法は2通り考えられる。
1つは新規データ$x'$を観測した際に、各変数の異常度を計算する。これは、「他の変数から期待される値とどの程度異なっているか」を示す量となる。
もう1つは、新たなデータ集合$D'$が得られた際に、正常時のデータ$D$からの食い違いを分析する場合。この場合、$i$番目の変数の異常度としては、$p(x_i \mid x_{-i}, D)$ と $p(x_i \mid x_{-i}, D')$のKLダイバージェンスを異常度として用いるのが良い。
