シンプルなレイトレーサーを実装してみる

この記事は Akatsuki Advent Calendar 2017 の21日目の記事です。

背景

最近はARにおける3Dグラフィックスをテーマとして取り組んでいます（具体的なアウトプット事例はこちら）。AR上での写実性の向上に関する論文を読んでいると、レンダラのアルゴリズムとしてラスタライズではなくレイトレーシング（をベースとする写実的な描画手法）を採用している研究が複数見つかります*1 。今回はそのキャッチアップを兼ねて、実際に手を動かして基本的なレイトレーサーを実装してみました。

先にレンダリング結果

ゲームエンジンやライブラリ未使用、スクラッチのC++コードのみで描画。

レイトレーシングについて

カメラから画素を経由してレイ（視線）を飛ばし、レイの物体との衝突や反射状況などを調べ経路を計算していき、最終的な画素色を決定していく手法。

メリット

• 写実的な描画が可能
• 鏡面反射表現に優れる
• ラスタライズベースでは難しい複数回の反射や屈折なども再現可能
• アルゴリズムに一貫性をもたせやすい
• 応用手法にしても「レイを全ての中心として衝突、反射をシミュレートしていく」という骨子は変わらない
• 精度を画素単位で制御可能
• 省メモリ

デメリット

• 計算時間が嵩みやすい
• 画素単位で複数回（多くは大量）のレイを飛ばすため。この理由のために基本的にはオフラインレンダリング、つまり映像・映画などの文脈で使われるのが主流。

本来ARで利用するには実時間描画（60FPS）が必須であるが、今回は第一歩として完全にオフライン想定。

各クラスの説明と実装

※ 座標は右手座標系を使う

Ray

• レイの管理
• レイはシンプルな直線なので、単純に

p(t) = \vec{A}_{origin} + t\vec{B}_{dir}

として考える。なお、

$\vec{A}_{origin}$ ... レイの原点

$\vec{B}_{dir}$ ... レイの方向

とする。

ray.h

class ray {
    public: ray() {}
    // aからbに向かうレイ
    ray(const vec3& a, const vec3& b) { A = a; B = b; }
    vec3 origin() const { return A; }
    vec3 direction() const { return B; }
    vec3 point_at_parameter(float t) const { return A + t * B; }

    vec3 A;
    vec3 B;
};

Sphere

• 球体オブジェクト
• レイとの衝突可否/衝突地点を計算する
• 基底にHitableを持つ（レイと衝突し得る3Dオブジェクト全てが対象）

球とレイの衝突

中心 $\vec{C}_{center} = (c_x, c_y, c_z)$ の球について、

(x-c_x)^2 + (y-c_y)^2 + (z-c_z)^2 = R^2

が成り立つ時、点 $\vec{p} = (x, y, z)$ は球の表面にあると言える（球の方程式）。

また、

(x-c_x)^2 + (y-c_y)^2 + (z-c_z)^2

= (x-c_x)(x-c_x) + (y-c_y)(y-c_y) + (z-c_z)(z-c_z)

= ((x, y, z) - (c_x, c_y, c_z))\cdot((x, y, z) - (c_x, c_y, c_z))

= (\vec{p} - \vec{C}_{center})\cdot(\vec{p} - \vec{C}_{center})

といえるので、球方程式を変換して

(\vec{p} - \vec{C}_{center})\cdot(\vec{p} - \vec{C}_{center}) = R^2

が成り立つ。
あとは、この方程式と先述のレイの方程式

p(t) = \vec{A}_{origin} + t\vec{B}_{dir}

を連立させることで、未知数 $t$ について解くことが出来る。

(p(t) - \vec{C})\cdot(p(t) - \vec{C}) = R^2

(\vec{A}_{origin} + t\vec{B}_{dir} - \vec{C}_{center})\cdot(\vec{A}_{origin} + t\vec{B}_{dir} - \vec{C}_{center}) = R^2

最終的に

t^2\vec{B}\cdot\vec{B} + 2t\vec{B}\cdot(\vec{A}-\vec{C}) + (\vec{A}-\vec{C})\cdot(\vec{A}-\vec{C}) - R^2 = 0

と展開できるので、これを解の公式

x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}

で解いてやればよい。

sphere.h

class sphere: public hitable {
    public: sphere() {}
    sphere(vec3 cen, float r, material *m): center(cen),
    radius(r),
    mat_ptr(m) {};
    virtual bool hit(const ray& r, float tmin, float tmax, hit_record& rec) const;
    vec3 center;
    float radius;
    material * mat_ptr;
};

bool sphere::hit(const ray& r, float t_min, float t_max, hit_record& rec) const {
    // 球とレイが衝突するかどうかを2次方程式の連立で解く
    // レイ: p(t) = A + tB
    // 球: (x-c_x)^2 + (y-c_y)^2 + (z-c_z)^2 = R^2
    //   -> (p-C)･(p-C) = R^2
    // この2つの連立により未知数tについて解く
    vec3 oc = r.origin() - center;
    float a = dot(r.direction(), r.direction());
    float b = 2.0 * dot(oc, r.direction());
    float c = dot(oc, oc) - radius * radius;
    // 判別式
    float discriminant = b * b - 4.0 * a * c;
    // 判別式が正の値の場合、実数解を2つ持つ
    // 0の場合は、実数解1つ、つまり端に衝突の時なので除く
    // また、正確に0でなく、浮動小数点近似値（0.00001等）の可能性もあるので、本来はt_minを0.001等に制限したい。
    if (discriminant > 0) {
        // 実数解1つ目
        float temp_t = (-b - sqrt(discriminant)) / (2.0 * a);
        if (temp_t < t_max && temp_t > t_min) {
            // temp_tは解の公式の解
            rec.t = temp_t;
            // 衝突点を取得
            rec.p = r.point_at_parameter(rec.t);
            // 法線は半径で割ることで単位ベクトル化
            rec.normal = (rec.p - center) / radius;
            rec.mat_ptr = mat_ptr;
            return true;
        }
        // 実数解2つ目
        temp_t = (-b + sqrt(discriminant)) / (2.0 * a);
        if (temp_t < t_max && temp_t > t_min) {
            rec.t = temp_t;
            rec.p = r.point_at_parameter(rec.t);
            rec.normal = (rec.p - center) / radius;
            rec.mat_ptr = mat_ptr;
            return true;
        }
    }
    return false;
}

Material

• オブジェクトごとの材質
• 今回は拡散反射、鏡面反射、屈折に対応する

拡散反射

今回は単純にランダム方向への反射で拡散面を近似する（ランバート反射を用いないのは、今回は光源を背景（空）全体の無指向性光源として近似しているため）。衝突点に接する単位円半径内に含まれるランダムな点を選び、衝突点からそちらへ向かうベクトルを拡散反射ベクトルとする。

material.h

vec3 random_in_unit_sphere() {
    vec3 p;
    do {
        p = 2.0 * vec3(drand48(), drand48(), drand48()) - vec3(1, 1, 1);
    } while (p.squared_length() >= 1.0);
    return p;
}

// 拡散反射
class lambertian: public material {
    public:
        // a: albedo、反射率、吸収されない入射光の割合
        lambertian(const vec3& a): albedo(a) {}
        virtual bool scatter(const ray& r_in,
            const hit_record& rec, vec3& attenuation, ray& scattered) const {
            // 拡散反射のシミュレート
            // 衝突地点の法線と、それを中心にした擬似的な円を考え、その円内のランダムな位置を取得
            vec3 target = rec.p + rec.normal + random_in_unit_sphere();
            scattered = ray(rec.p, target - rec.p);
            attenuation = albedo;
            return true;
        }
        vec3 albedo;
};

鏡面反射

反射ベクトルを求める式は、

があるとき

\vec{r} = \vec{v} + 2\vec{b}

また

\vec{b} = (-\vec{v} \cdot \vec{n})\cdot \vec{n}

となる（内積で大きさを求め、さらに $\vec{n}$ をかけてベクトル化）ので、最終的に

\vec{r} = \vec{v} - 2(\vec{v} \cdot \vec{n})\cdot \vec{n}

と分かる。
また、反射の（不）鮮明度の近似として、$fuzz$ 係数を設けて拡散反射と同様の成分を加えられるようにする。

material.h

vec3 reflect(const vec3& v, const vec3& n) {
    return v - 2 * dot(v, n) * n;
}

class metal: public material {
    public:
        // a: albedo f: 反射の不鮮明さ
        metal(const vec3& a, float f): albedo(a) {
            if (f < 1) fuzz = f;
            else fuzz = 1;
        }
        virtual bool scatter(const ray& r_in, const hit_record& rec, vec3& attenuation, ray& scattered) const {
            // 反射のシミュレート
            vec3 reflected = reflect(unit_vector(r_in.direction()), rec.normal);
            scattered = ray(rec.p, reflected + fuzz * random_in_unit_sphere());
            attenuation = albedo;
            return (dot(scattered.direction(), rec.normal) > 0);
        }
        vec3 albedo;
        float fuzz;
};

屈折

屈折方向は、光が入射する物体の屈折率に応じて決まり、スネルの法則 をもとに求めることができる。
また一般的な屈折物質では同時に反射も生じるが、入射光のうちどれだけの割合が反射するか、フレネルの法則 によって求める。

スネルの法則

屈折率 $\eta_1$ の物質1から屈折率 $\eta_2$ の物質2へ光が入射する時、入射角 $\theta_1$ と屈折角 $\theta_2$ の間には以下の関係が成立する。

\eta_1\sin\theta_1 = \eta_2\sin\theta_2

この法則を元に、以下のような屈折を考える。

スネルの法則に基づき変換すると

\eta_1\mid\vec{i} - \cos\theta_1\vec{n}\mid = \eta_2\mid\vec{f} + \cos\theta_2\vec{n}\mid

※ 図中の $\cos\theta_1\vec{n}$ は実際は単位進行ベクトルの逆ベクトル $-\vec{i}$ と単位法線ベクトル $\vec{n}$ の内積 $(-\vec{i}\cdot\vec{n})$ にベクトル $\vec{n}$ を乗じたものなので、今回は $-\cos\theta_1\vec{n}$ として扱う。

この時 $\mid\vec{i} - \cos\theta_1\vec{n}\mid$ と $\mid\vec{f} + \cos\theta_2\vec{n}\mid$ はどちらも正の向きを持つため絶対値をそのまま外すことが出来る。

\eta_1(\vec{i} - \cos\theta_1\vec{n}) = \eta_2(\vec{f} + \cos\theta_2\vec{n})

ここから $\vec{f}$ について整理し、

\vec{f} + \cos\theta_2\vec{n} = \frac{\eta1}{\eta_2}(\vec{i} - \cos\theta_1\vec{n})

\vec{f} = \frac{\eta1}{\eta_2}(\vec{i} - \cos\theta_1\vec{n}) - \cos\theta_2\vec{n}

となる。またスネルの法則から $\cos\theta_2$ を得る。

\eta_1\sin\theta_1 = \eta_2\sin\theta_2

\eta_2^2\sin^2\theta_2 = \eta_1^2\sin^2\theta_1

\eta_2^2(1 - \cos^2\theta_2) = \eta_1^2(1 - \cos^2\theta_1)

1 - \cos^2\theta_2 = (\frac{\eta_1}{\eta_2})^2(1 - \cos^2\theta_1)

\cos^2\theta_2 = 1 - (\frac{\eta_1}{\eta_2})^2(1 - \cos^2\theta_1)

\cos\theta_2 = \pm\sqrt{1 - (\frac{\eta_1}{\eta_2})^2(1 - \cos^2\theta_1)}

実際には、$\cos\theta_2$ つまり屈折角が負になることは無いので、

\cos\theta_2 = \sqrt{1 - (\frac{\eta_1}{\eta_2})^2(1 - \cos^2\theta_1)}

あとは、先ほど求めた $\vec{f}$ に $\cos\theta_2$ を代入することで、

\vec{f} = \frac{\eta_1}{\eta_2}(\vec{i} - \cos\theta_1\vec{n}) - \cos\theta_2\vec{n}

\vec{f} = \frac{\eta_1}{\eta_2}(\vec{i} - \cos\theta_1\vec{n}) - \vec{n}\sqrt{1 - (\frac{\eta_1}{\eta_2})^2(1 - \cos^2\theta_1)}

とすることで屈折ベクトルが得られた。

material.h

// 屈折
// スネルの法則に基づく
// 屈折率が大きくなると実数解がなくなる問題がある。その際はすべての光が反射するものとして扱う
// ni_over_nt: 入射前物体の屈折率 / 入射後物体の屈折率
bool refract(const vec3& v, const vec3& n, float ni_over_nt, vec3& refracted) {
    vec3 uv = unit_vector(v);
    float dt = dot(uv, n);
    float discriminant = 1.0 - ni_over_nt * ni_over_nt * (1 - dt * dt);
    if (discriminant > 0) {
        refracted = ni_over_nt * (uv - n * dt) - n * sqrt(discriminant);
        return true;
    } else {
        return false;
    }
}

フレネルの法則

フレネルは入射光の反射・屈折の割合を表すが、実際のアルゴリズムとしてはSchlickの近似式が用いられることが多い。

F_r(\theta) \approx F_0 + (1 - F_0)(1 - cos\theta)^5

フレネル反射率 $F_r$ は、入射角が $\theta$ の時入射光がどれだけの割合で反射されるかを表す。この時、$F_0$ は入射角が0、つまり垂直入射時の反射率を表しており、以下の式で求めることが出来る。

F_0 = \frac{(\eta_1 - \eta_2)^2}{(\eta_1 + \eta_2)^2} = (\frac{\eta_1 - \eta_2}{\eta_1 + \eta_2})^2

例えば水の場合、視線（レイ）の入射角が深くなるにつれ反射特性が強くなるということは直感的にも理解できるが、その現象もフレネルによって表すことが出来る。

material.h

// フレネル
// 反射光と屈折光の分配比率
float schlick(float cosine, float ref_idx) {
    float r0 = (1 - ref_idx) / (1 + ref_idx);
    r0 = r0 * r0;
    return r0 + (1 - r0) * pow((1 - cosine), 5);
}

material.h

// ガラスなど屈折物質
class dielectric: public material {
    public:
    // ri: 物体の屈折率
    dielectric(float ri): ref_idx(ri) {}
    virtual bool scatter(const ray& r_in,
        const hit_record& rec, vec3& attenuation, ray& scattered) const {
        vec3 outward_normal;
        vec3 reflected = reflect(r_in.direction(), rec.normal);
        float ni_over_nt;
        // 減衰は常に1
        attenuation = vec3(1.0, 1.0, 1.0);
        vec3 refracted;
        float reflect_prob;
        float cosine;
        // 入射光と衝突面法線の内積が0より大きいなら、空気から物体へ入っていくベクトルなので、ni_over_ntは空気屈折率/物体屈折率
        if (dot(r_in.direction(), rec.normal) > 0) {
            outward_normal = -rec.normal;
            ni_over_nt = ref_idx;
            // フレネル用
            cosine = ref_idx * dot(r_in.direction(), rec.normal) / r_in.direction().length();
        } else {
            // 入射光と衝突面法線の内積が0以下なら、物体から空気へ出ていくなので、ni_over_ntは物体屈折率/空気屈折率
            outward_normal = rec.normal;
            ni_over_nt = 1.0 / ref_idx;
            // フレネル用
            cosine = -dot(r_in.direction(), rec.normal) / r_in.direction().length();
        }
        if (refract(r_in.direction(), outward_normal, ni_over_nt, refracted)) {
            reflect_prob = schlick(cosine, ref_idx);
        } else {
            reflect_prob = 1.0;
        }
        if (drand48() < reflect_prob) {
            scattered = ray(rec.p, reflected);
        } else {
            scattered = ray(rec.p, refracted);
        }
        return true;
    }
    float ref_idx;
};

Camera

• カメラ（＝視線）の管理
• アングル、視野角の設定

• DoF（被写界深度）
• レンズ口径が大きくなるほど、サンプリング点がブレるようにする（ためにレイの出射位置をずらす）

camera.h

// 単位円上の点でかつある程度内側に近い点を返す
vec3 random_in_unit_disk() {
    vec3 p;
    do {
        p = 2.0 * vec3(drand48(), drand48(), 0) - vec3(1, 1, 0);
    } while (dot(p, p) >= 1.0); // 内積が1以上、つまりある程度外側の座標の場合はやりなおし
    return p;
}

// 視界の管理クラス
class camera {
    public:
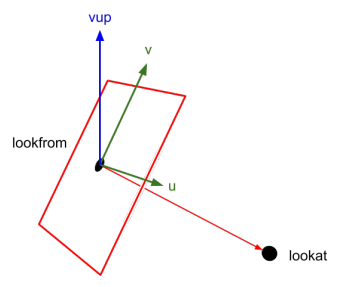
        // lookfrom: カメラ配置位置
        // lookat: 視線を向ける点
        // vfov: vertical_fov、つまり縦方向の視野角
        // vup: 上向き（ロール回転を固定する必要があるため）
        // aspect: アス比（横/縦）
        // aperture: 口径＝レンズの大きさ、大きいと取り込む光は増え、ボケる
        // focus_dist: 焦点距離
        camera(vec3 lookfrom, vec3 lookat, vec3 vup, float vfov, float aspect, float aperture, float focus_dist) {
            // レンズ半径（レンズ口径 / 2）
            lens_radius = aperture / 2;
            // 視野角をラジアンへ変換
            float theta = vfov * M_PI / 180;
            // tanで半分の高さ取得
            float half_height = tan(theta / 2);
            // アス比を考慮して横幅取得
            float half_width = aspect * half_height;
            origin = lookfrom;
            // 奥行方向（右手座標系のため手前に戻ってくる方向であることに注意）
            w = unit_vector(lookfrom - lookat);
            // vupとwの作る平行四辺形に直行するベクトル＝x軸方向
            u = unit_vector(cross(vup, w));
            // wとuに直行するベクトル＝y軸方向
            v = cross(w, u);
            // focus_dist（焦点距離）が大きいほど画角は狭まる
            lower_left_corner = origin - half_width * focus_dist * u - half_height * focus_dist * v - focus_dist * w;
            horizontal = 2 * half_width * focus_dist * u;
            vertical = 2 * half_height * focus_dist * v;
        }
    ray get_ray(float s, float t) {
        return ray(origin, lower_left_corner + s * horizontal + t * vertical - (origin));
        // 被写界深度のため、レイを一点からではなく、lookfromの周囲の円形領域から飛ばす
        /*
        vec3 rd = lens_radius * random_in_unit_disk();
        vec3 offset = u * rd.x() + v * rd.y();
        return ray(origin + offset, lower_left_corner + s * horizontal + t * vertical - (origin + offset));
        */
    }
    vec3 origin;
    vec3 lower_left_corner;
    vec3 horizontal;
    vec3 vertical;
    vec3 u, v, w;
    float lens_radius;
};

Renderer

• 描画処理の実行
• アンチエイリアス
• SSAA。1ピクセルに対して複数のレイを飛ばし、レイ毎に僅かにサンプリング点をずらす。最後にサンプルした色の平均を取る

main.cpp

// レイとの衝突に応じて色味を決める
vec3 color(const ray& r, hitable *world, int depth) {
    hit_record rec;
    if (world -> hit(r, 0.001, MAXFLOAT, rec)) {
        ray scattered;
        vec3 attenuation;
        if (depth < 50 && rec.mat_ptr -> scatter(r, rec, attenuation, scattered)) {
            return attenuation * color(scattered, world, depth + 1);
        } else {
            // トレース打ち切り
            return vec3(0, 0, 0);
        }
    } else {
        // 未衝突時は背景（空）
        vec3 unit_direction = unit_vector(r.direction());
        float t = 0.5 * (unit_direction.y() + 1.0);
        return (1.0 - t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
    }
}
int main() {
    int nx = 600;
    int ny = 300;
    int ns = 100;
    std::cout << "P3\n" << nx << " " << ny << "\n255\n";
    hitable *world = random_scene();
    vec3 lookfrom(12, 2.08, 2);
    vec3 lookat(0, 0, 0);
    float dist_to_focus = 10.0;
    float aperture = 0.1;
    camera cam(lookfrom, lookat, vec3(0, 1, 0), 20, float(nx) / float(ny), aperture, dist_to_focus);
    for (int j = ny - 1; j >= 0; j--) {
        for (int i = 0; i < nx; i++) {
            vec3 col(0, 0, 0);
            // アンチエイリアスのため、1ピクセル辺りに複数の点を選び、それらの点にレイを飛ばし、色の平均を取る。
            for (int s = 0; s < ns; s++) {
                float u = float(i + drand48()) / float(nx);
                float v = float(j + drand48()) / float(ny);
                ray r = cam.get_ray(u, v);
                vec3 p = r.point_at_parameter(2.0);
                col += color(r, world, 0);
            }
            col /= float(ns);
            // ガンマ補正。近似として1/2乗つまり根号を取る。
            col = vec3(sqrt(col[0]), sqrt(col[1]), sqrt(col[2]));
            int ir = int(255.99 * col[0]);
            int ig = int(255.99 * col[1]);
            int ib = int(255.99 * col[2]);
            std::cout << ir << " " << ig << " " << ib << "\n";
        }
    }
}

まとめ

シンプルなアルゴリズム、小さなコードベースで写実性な描画が行えるのは魅力的。実際レイトレーシングは近年のハードウェアの進化とあわせて活用範囲が広がってきているので、さらに深掘りしていきたいです。

今回の課題（不足）点

• 間接光が考慮されていない
• 高速化の工夫がないため低速
• CPU実装のため低速

今後やりたいこと

• パストレーシングやフォトンマッピングのような、間接光を考慮した実装（グローバルイルミネーション）
• 高速なアルゴリズムの模索
• ハードウェア化（GPU上に移植）
• 異なるトレーシング手法（具体的にはレイマーチング）との比較、使い分け

参考

Ray Tracing in One Weekend
http://a.co/gJohrF3

Simple Renderer
http://kagamin.net/hole/simple/

Argorithms ( Ray Tracing )
http://www.not-enough.org/abe/manual/argo/ray.html

Chapter1. レイトレーシング法とは何か | The Textbook of RayTracing
https://www.vcl.jp/~kanazawa/raytracing/?page_id=50

接平面の方程式
http://examist.jp/mathematics/space-equation/setuheimen/

Chapter9. 光の屈折 | The Textbook of RayTracing @TDU
https://www.vcl.jp/~kanazawa/raytracing/?page_id=478

フレネル反射率について
http://d.hatena.ne.jp/hanecci/20130525/p3

Disclaimer

本文中のコードでヘッダに実装が書いてあるのは、参考にさせて頂いた先人の例を真似て。レイトレはそこまで大きなコードベースにならないので、ざっくり書かれることが多いのでしょうか。

memo

*1: 例えば以下など。
Natural Environment Illumination: Coherent Interactive Augmented Reality for Mobile and Non-Mobile Devices
http://www2.in.tu-clausthal.de/~cgstore/publications/2017_Rohmer_ISMAR_AuthorsVersion.pdf

Efficient and robust radiance transfer for probeless photorealistic augmented reality
https://www.ece.ucsb.edu/~psen/Papers/VR2014_EfficientRadianceTransferAR.pdf

Differential Irradiance Caching for Fast High-Quality Light Transport Between Virtual and Real Worlds
http://peterkan.com/download/ismar2013.pdf