この記事は Akatsuki Advent Calendar 2018 の18日目の記事です。
はじめに
CNNで比較的人気の高いジャンルであるStyle Transferについて、主要な論文をまとめて紹介します。
Style Transferとは
構造を担保するコンテンツ画像と、画風を担保するスタイル画像の2つを入力にとり、前者の構造と後者の画風を併せ持つ合成画像を出力する仕組みです。
もともと Image Analogies や Texture Synthesis といったアルゴリズムが研究されていましたが、近年では深層ニューラルネットワーク(DNN、深層学習)を活用して高い品質を実現する研究が多く発表されています。
Image Style Transfer Using Convolutional Neural Networks
Gatysらによって2016年に発表された論文です。Style Transferにニューラルネットワークを活用するアプローチの火付け役となりました。
アーキテクチャ
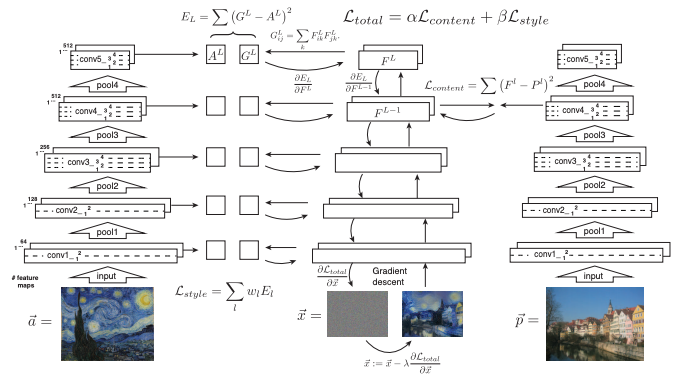
まず左右の訓練済VGGネットワークにコンテンツとスタイル画像をそれぞれ入力し、その途中の特徴マップから各「画像らしさ」を表すベクトルを抜き出して損失関数を定義します。そしてその損失を最小化する形で最適化を進めていくのですが、本手法における最適化対象は重みではなく画像のピクセル自体になります。これにより、最適化が完了した時点で画像が生成されることになります。
では、以下で具体的な損失関数を見ていきます。
Content loss
コンテンツ損失では、コンテンツ画像と生成画像から特定の特徴マップ1層を抜き出してその平均二乗誤差を損失とします。
L_{content}(\vec{p},\vec{x},l) = \frac{1}{2} \sum_{i,j} (F_{ij}^l - P_{ij}^l)^2
$F_{ij}^l$ … 生成画像の $l$ 層における特徴マップの位置 $i,j$ でのアクティベーション(特徴表現)
$P_{ij}^l$ … コンテンツ元画像の(同上)
Style loss
スタイル損失は、個々の層でカーネルを適用した出力結果(特徴マップ)についてそれぞれの間で相関を取ることで、特徴ごとの類似度、つまりその画像らしさを表した表現を使います。相関を取るには2つの特徴マップ間で内積を取ることになりますが、これはグラム行列と呼ばれます。
G_{ij}^l = \sum_{k} F_{ik}^l F_{jk}^l
そして、生成画像の特徴マップのグラム行列の結果とスタイル元画像のグラム行列の差分を取り平均二乗誤差を求めます。
E_l = \frac{1}{4N_{l}^2 M_{l}^2} \sum_{i,j} (G_{ij}^l - A_{ij}^l)^2
$N_{l}$ … 特徴マップの数
$M_{l}$ … 特徴マップのサイズ(縦x横)
あとは層ごとの損失の線形和をスタイルの合計損失とします。
L_{style}(\vec{a}, \vec{x}) = \sum_{l=0}^L w_l E_l
ポイント
まずCNNでは、ネットワークの層が進むにつれてより抽象的な特徴をキャプチャするようになっています(逆に言うと、浅い層では例えば「直線」や「ななめ線」などごく具体的な特徴が学習されています)。

DL-Tutorial-NIPS2015 より
ここから、「画像の構造の特徴」を表現するためのコンテンツ損失関数には、深い層の表現を1層抜き出して採用しています。一方でスタイルについては全ての層について特徴間の相関を得ることで、各特徴の組み合わさり方、つまりは「画像の画風」という抽象的なものを表現できるというアイデアに基づいた損失の設定になっているのがポイントです。
まとめ
VGGのような既存の画像認識ネットワークの途中の層で「画像らしさ」を捉えられているはずだと仮説した点、それをグラム行列のような表現で実際に効果のある損失関数を定義した点が本論文の新規性になっています。
Perceptual Losses for Real-Time Style Transfer and Super-Resolution
Johnsonらによって2016年に発表された論文です。Gatysの手法の欠点である処理速度を大きく改善しており、こちらも後続のStyle Transfer関連の論文でほぼ必ず参照される有名な論文です。
アーキテクチャ
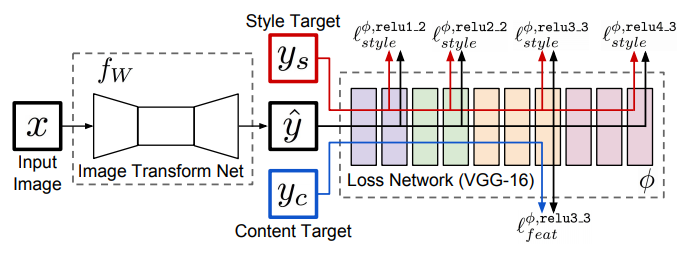
このように変換ネットワーク $f_w$(重み $w$)と、損失ネットワーク $\phi$ の2つのネットワークから構成されています。
実際には損失ネットワーク $\phi$ はGatysの時に用いた構成とほぼ同じで、訓練済のVGG-16を通してスタイルとコンテンツ画像、そして生成画像の特徴を抜き出します。そしてその値を基にして変換ネットワーク $f_w$ の損失関数を用意し、$f_w$ を最適化していきます。
- 変換ネットワーク $f_w$ は、画像 $x$ を入力にとり、画像 $\hat{y}$ を出力($\hat{y} = f_w(x)$)
- 損失ネットワーク $\phi$ はコンテンツ損失 $l_{feat}^{\phi}$ とスタイル損失 $l_{style}^{\phi}$ を持つ
- これらの損失の線形和を最小化する画像を出力する変換ネットワークを訓練出来るように損失関数を定義
W^{*} = argmin_{W} E_{x,\{y_i\}} [\sum_{i=1} λ_i l_i(f_W(x), y_i)]
損失ネットワーク
基本的なアイデアはGatysの手法と同じです。
コンテンツ損失
高次元の1層を選ぶことで構造的特徴のみを取り出し、平均二乗誤差を取ります。
l_{feat}^{\phi, j} (\hat{y}, y) = \frac{1}{C_j H_j W_j} ||\phi_j(\hat{y}) - \phi_j(y) ||_2^2
$\phi_j(\hat{y})$ ... 入力 $\hat{y}$ に対する $j$ 番目の特徴マップ
$C_j, H_j, W_j$ ... $j$ 番目の特徴マップのチャネル数、高さ、横幅
スタイル損失
各層ごとにグラム行列を取ってスタイル特徴を取り出して損失とします。
グラム行列:
G_j^{\phi}(x)_{c,c'} = \frac{1}{C_j H_j W_j} \sum_{h=1}^{H_j} \sum_{w=1}^{W_j} \phi_j (x)_{h,w,c} \phi_j (x)_{h,w,c'}
スタイル損失:
l_{style}^{\phi, j} (\hat{y}, y) = ||G_j^{\phi}(\hat{y}) - G_j^{\phi}(y) ||_F^2
スタイル損失ではフロベニウスノルム $F$ を取っていますが、ここでは行列の成分ごとに $m \times n$ 成分のベクトルのノルムとみなして考えるため実質的にL2ノルムと同等です(=平均二乗誤差を取る)。
What is the difference between the Frobenius norm and the 2-norm of a matrix?
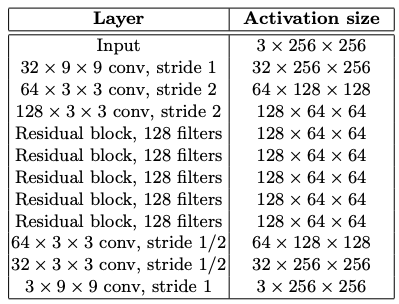
変換ネットワーク
- プーリング層を避け、代わりにストライドの幅で出力する特徴マップのサイズをコントロール
- Residual blocksの導入
- 中間層をスキップする接続を導入することで、圧縮する前の情報を直接Decoderの中間層の入力に加えられるような工夫により、情報圧縮による出力精度の低下の防止を図る
- Batch Normalizationの導入
- 入力層だけでなく中間層も正規化することで、学習速度の向上と安定を図る
Batch Normalizationについては次の論文でも使うことになるので以下説明を加えます。
Batch Normalization
- 特徴の統計を正規化(平均を0、分散を1に)することでNNの訓練をスムーズにする
- 個々の特徴のチャネル(特徴マップ)単位で正規化(平均を0、分散を1に)する
- 内部共変量シフト(各層間での入力分布のばらつき)を抑えることで、本質的なパラメータの変化そのものに注力出来るようにして、学習を高速化する。また入力が大きくなりすぎることで非線形関数が飽和することによって起こる勾配消失問題を回避する。
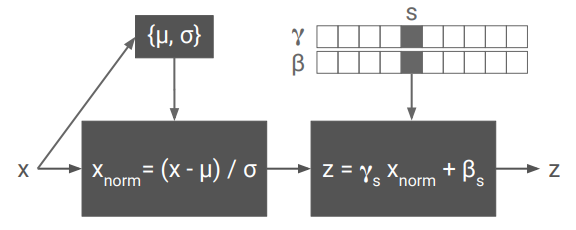
BN(x) = \gamma(\frac{x-\mu(x)}{\sigma(x)}) + \beta
$x \in \mathbb{R}^{N \times C \times H \times W}$ ... バッチ単位の入力
$N$ ... バッチサイズ
$\gamma, \beta \in \mathbb{R}^C$ ... 学習対象パラメータ
$\mu(x), \sigma(x) \in \mathbb{R}^C$ ... 平均, 標準偏差
\mu_c(x) = \frac{1}{NHW} \sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W x_{nchw}
\sigma_c(x) = \sqrt{\frac{1}{NHW} \sum_{n=1}^N \sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_c(x))^2 + \epsilon}
- $\gamma$, $\beta$ の役割は、正規化後の値をそれぞれスケーリング、シフト(平行移動)すること。
- ただ入力を正規化するだけだと、その層の表現力を制限してしまう可能性があるため。例えば、Sigmoidの入力が0-1に限定されると、その出力は非線形部分には到達せず、中央の線形部分の領域に限定されてしまう。
- BNはミニバッチ学習の間利用され、推論時は使わない。
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
合計損失
\hat{y} = argmin_y \lambda_c l_{feat}^{\phi, j} (y, y_c) + \lambda_s l_{style}^{\phi, J} (y, y_s)
上で書いた変換ネットワークの損失関数の中に内包されるものと見ることも出来ます。
定性評価
右下の例などは微妙に劣っているようにも見えますが、おおむね同程度の品質が保たれています。
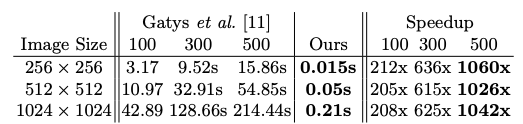
定量評価(実行速度)
Gatysの手法と比較して3桁倍高速です。
まとめ
Gatysの手法に変換ネットワークを加えることで実行時はfeed-forwardの処理のみで推論(つまり画像変換)でき、大幅な処理の高速化を達成した点がポイントです。ただし変換ネットワークは1つのスタイルに固定されている(スタイルを変更する場合は再訓練が必要)という欠点があります。
発展的なStyle Transfer
ここまでのGatysとJohnsonの手法を基礎として、後続の改良手法を紹介していきます。
Instance Normalization: The Missing Ingredient for Fast Stylization
Ulyanovらによって2017年に発表された論文です。Batch NormalizationをInstance Normalizationに変えるとStyle Transferの質において大きな向上が達成されることを提案しています。
Instance Normalization
Instance Normalization以下2点がBatch Normalizationと異なる正規化手法です。
- 1画像サンプルに紐づくチャネル(特徴マップ)単位で正規化する
- Instance Normalization層は推論時にも利用される
IN(x) = \gamma(\frac{x-\mu(x)}{\sigma(x)}) + \beta
\mu_{nc}(x) = \frac{1}{HW} \sum_{h=1}^H \sum_{w=1}^W x_{nchw}
\sigma_{nc}(x) = \sqrt{\frac{1}{HW} \sum_{h=1}^H \sum_{w=1}^W (x_{nchw} - \mu_nc(x))^2 + \epsilon}
Instance Normalizationを導入した結果として以下のような出力が得られています。

1段目:入力画像(コンテンツ、スタイル)
2段目:BatchNormalizationを用いた場合のJohnson(左)、Ulyanov(右)
3段目:InstanceNormalizationを用いた場合のJohnson(左)、Ulyanov(右)
INの場合比較的構造を捉えた上でスタイル変換が効いているように見えます。
A Learned Representation For Artistic Style
Dumoulinらによって2017年に発表された論文です。Instance Normalizationのパラメータ $\gamma, \beta$ をスタイルごとに異なるものとして学習させ、一度の訓練で複数のスタイルに適用できるようにする手法を提案しました。
以下のように $\gamma, \beta$ のパラメータのみ変えることで推論時に複数のスタイルを与えることが可能になります。
CIN(x; s) = \gamma^s(\frac{x-\mu(x)}{\sigma(x)}) + \beta^s
例えば4つのスタイルを学習させることで、実行時にパラメータの変更のみでスタイルを変更することが出来ます。スタイルを混ぜ合わせて中間的な表現を行うことも可能です。論文では一つのネットワークに32個のスタイルを訓練することに成功しています。

問題点としては、スタイル数が増えるほどパラメータ数も線形に増加していくこと、新しいスタイルに適応するには再訓練が必要であることが挙げられます。
Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization
Huangらによって2017年に発表された論文です。Instance Normalizationはスタイル特徴の統計量を正規化することでスタイル変換を行うもの、という解釈を加え、INを拡張した Adaptive Instance Normalization (AdaIN) を提案しています。AdaINはコンテンツ画像の平均と分散をスタイル画像のそれに置き換える操作となります。
Adaptive Instance Normalization
AdaIN(x, y) = \sigma(y)(\frac{x-\mu(x)}{\sigma(x)}) + \mu(y)
- コンテンツ入力 $x$ とスタイル入力 $y$ をとり、$x$のチャネル平均と分散を $y$ のものと一致するように揃える
- BN,IN,CINと違い、学習パラメータは不要。その代わりに $y$ から任意にアフィンパラメータを計算する
つまり、INは正規化された入力をどのようにスケーリング、シフトするかの係数を訓練によって決定していたが、AdaINでは直接的にスタイル入力 $y$ の統計値に入れ替えてやっているということになります。
アーキテクチャ
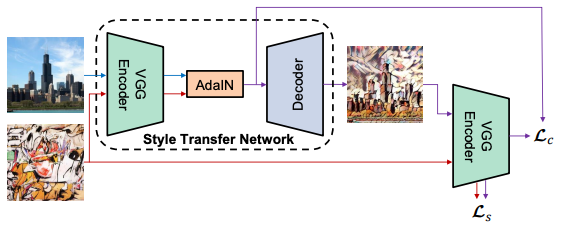
Johnsonの手法と同じく変換ネットワークと損失ネットワークが有り、変換ネットワークのbottleneck(EncoderとDecoderの中間)にAdaINが挟まっている構成だと考えると分かりやすいです。
- 変換ネットワーク $T$ はコンテンツ画像 $c$ と 任意のスタイル画像 $s$ を入力に取り、前者と後者のコンテンツを結合して合成
- エンコーダー $f$ は訓練済VGG-19の最初の数レイヤー(relu4_1まで)
- 特徴空間で画像をエンコードしたら、それらをコンテンツの特徴マップの平均を分散をスタイル特徴マップのそれに揃えるAdaINレイヤーに入れて、ターゲット特徴マップ $t$ を生成
t = AdaIN(f(c), f(s))
- デコーダー $g$ は $t$ を画像空間に戻すように訓練され、スタイル画像 $T(c, s)$ を生成
T(c, s) = g(t)
- デコーダーはほぼエンコーダーの反転。ノイズを減らすため、すべてのプーリング層はnearest upsamplingに入れ替えられている
- 横線のアーティファクトを避けるために、 $f$, $g$ 両方でreflection paddingを採用
損失関数
コンテンツ損失
L_c = || f(g(t)) - t ||_2
コンテンツ損失は、「変換ネットワークの出力 $f(g(t))$」とコンテンツ特徴としての「AdaINの出力 $t$」の差分を取っています。コンテンツ特徴として「コンテンツ画像をVGGに通して得た特徴」ではなく「AdaINの出力 $t$」を採用した理由は、実験の結果収束が早まることが分かったためとしています。
スタイル損失
L_s = \sum_{i=1}^L || \mu(\phi_i(g(t))) - \mu(\phi_i(s)) ||_2 + \sum_{i=1}^L || \sigma(\phi_i(g(t))) - \sigma(\phi_i(s)) ||_2
層ごとに「$g(t)$ の出力」と「スタイル画像」の平均と標準偏差をそれぞれ比較しています。またグラム行列を用いた場合も類似の結果になることが分かっているが、より統計的アルゴリズムとして可視化されている方(平均と標準偏差の各差分)を用いたとしています。
合計損失
コンテンツ損失とスタイル損失(任意の重み $\lambda$)の線形和になります。
L = L_c + \lambda L_s
まとめると、あるスタイルを入力して、その統計的特徴をコンテンツ画像に付与することで所望の画像が得られるようになる生成ネットワークを訓練する構成になっています。
定性評価
GatysやJohnsonの手法と近しい品質と言えます。5行目の例は品質が低めに見えますがスピード、柔軟性、品質のトレードオフがあることを考えると妥当としています。
定量評価
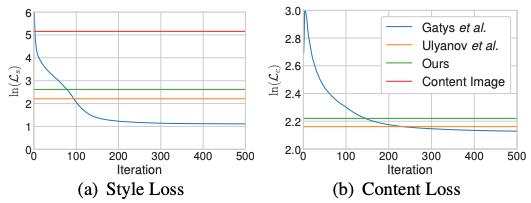
損失関数の収束の比較
- 合成画像の平均コンテンツ損失とスタイル損失
- テストデータセットからランダムに選択されたスタイル画像10枚とコンテンツ画像50枚で平均化されたもの
- Ulyanovよりわずかに高い
- Gatysの50-100イテレーションの時と同等の水準
- Ulyanovの手法では各ネットワークは個々のテストスタイル画像で訓練しているのに対し、本手法は訓練中にテスト用スタイルを見たことがないことを考慮すると、強力な一般化能力を備えていると言える
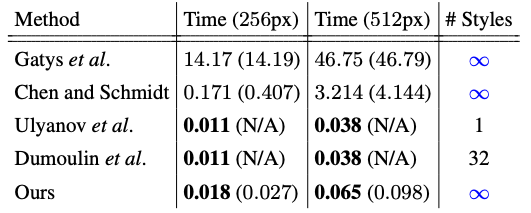
実行速度
- スタイル画像のエンコーディングを除き、256x256画像は56fps、512x512画像は15fps
- Gatysより3桁倍速い
- かつ、柔軟性の限られたfeed-forwardの手法UlyanovやDumoulinに匹敵する速度
Style Transferはスタイル品質、速度(訓練時/推論時)、柔軟性(一度の訓練で適用できるスタイルの数)の3つのトレードオフだと考えると、最後発である本手法は非常にバランスの良い手法だと言えます。
最後に
以上、近年のStyle Transferの中で有名な論文をポイントをかいつまんで紹介してきました。後続の論文は今回紹介したものが土台となっていることが多いので、これらを抑えておくと最新の論文もスムーズに読めるようになると思います。本当は動画に最適化したものやGANベースのものも紹介したかったのですが、長くなってきたのでまたの機会に。Style Transferに興味を持っている方々の一助となれば幸いです。